Lecture 13

Mergesort

MCS 275 Spring 2023
Emily Dumas

Lecture 13: Mergesort

Reminders and announcements:

  • Project 2 posted; due 6pm central Fri Feb 24.
  • Project 1 grading underway.
  • Homework 5 due tomorrow (notebook).

Project 2

Demo and discussion to supplement the project description.

Plan

  • Discuss the theory of
    • Divide and conquer
    • Sorting
    • Mergesort
  • Implement mergesort

Divide and conquer

A strategy that often involves recursion.

  • Split a problem into parts.
  • Solve for each part.
  • Merge the partial solutions into a solution of the original problem.

Not always possible or a good idea. It only works if merging partial solutions is easier than solving the entire problem.

Comparison sort

Suppose you have a list of objects that can be compared with ==, >, <.

You'd like to reorder them in increasing order.

This problem is called comparison sort. There are many solutions.

Mergesort

A divide-and-conquer solution to comparison sort.

It is a fast solution, often used in practice.

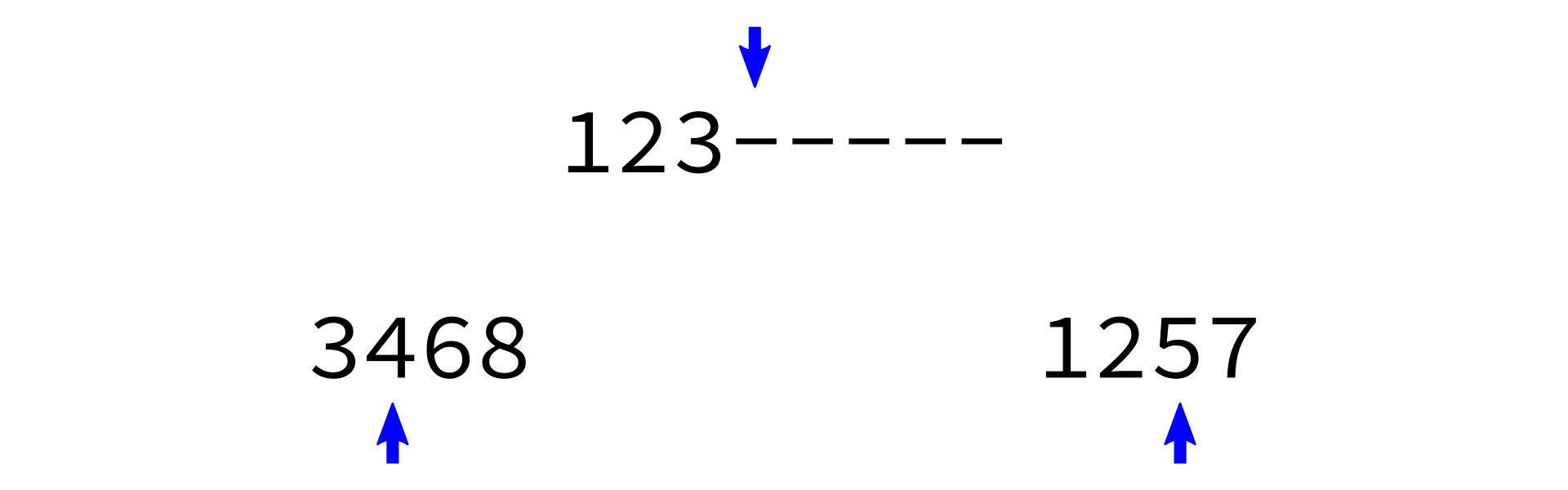
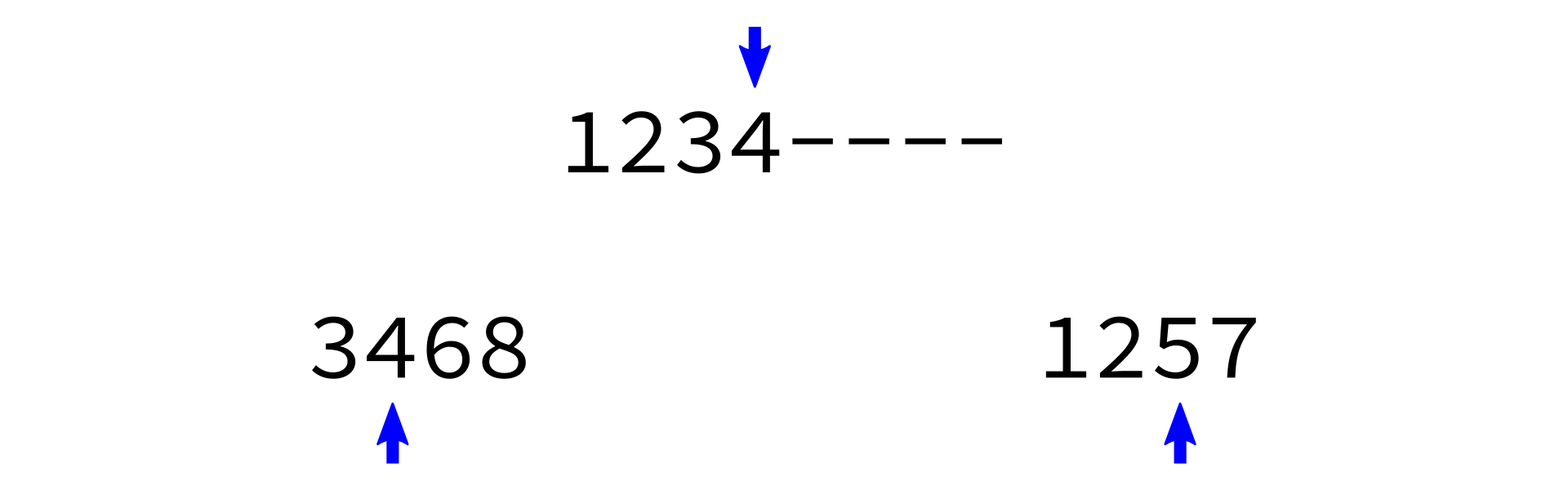
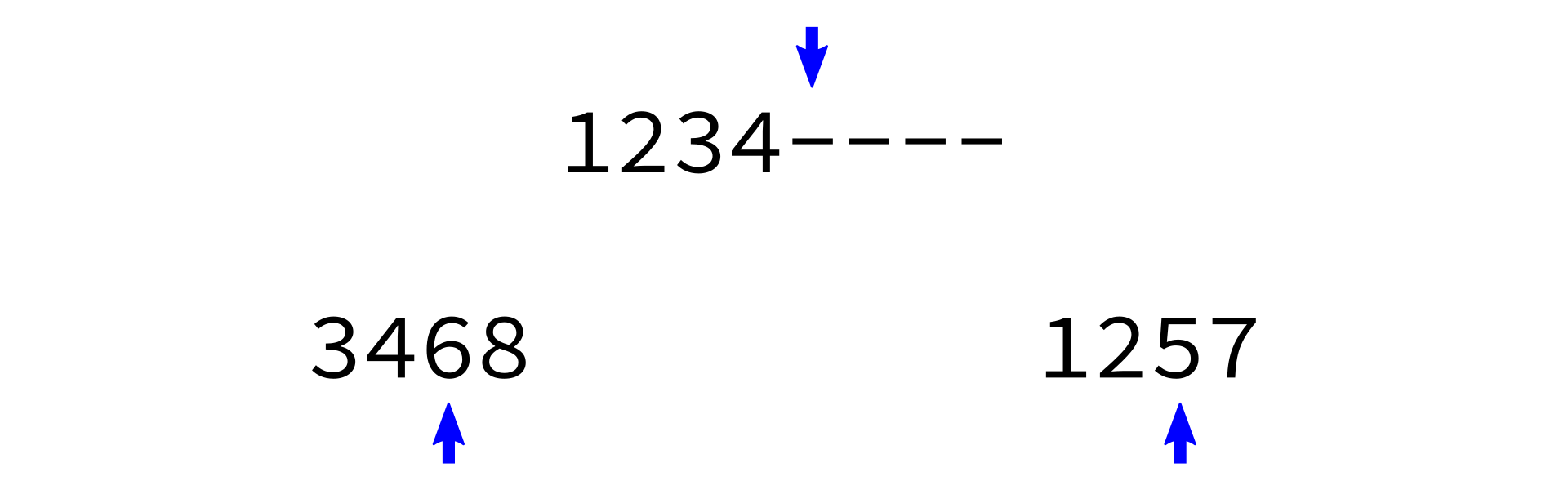
Key: It is pretty easy to take two sorted lists and merge them into a single sorted list.

So, let's divide our list into halves, sort each one (recursively), then merge them.

Now we'll formalize this.

Algorithm mergesort:

Input: list L whose elements support comparison.

Goal: return a list that contains the items from L but in sorted order.

  1. If L has 0 or 1 elements, return L
  2. Otherwise, divide L into rougly equal pieces L0 and L1.
  3. Recursively call mergesort on L0 and L1.
  4. Use merge to merge these sorted lists and return the result.

Mergesort example

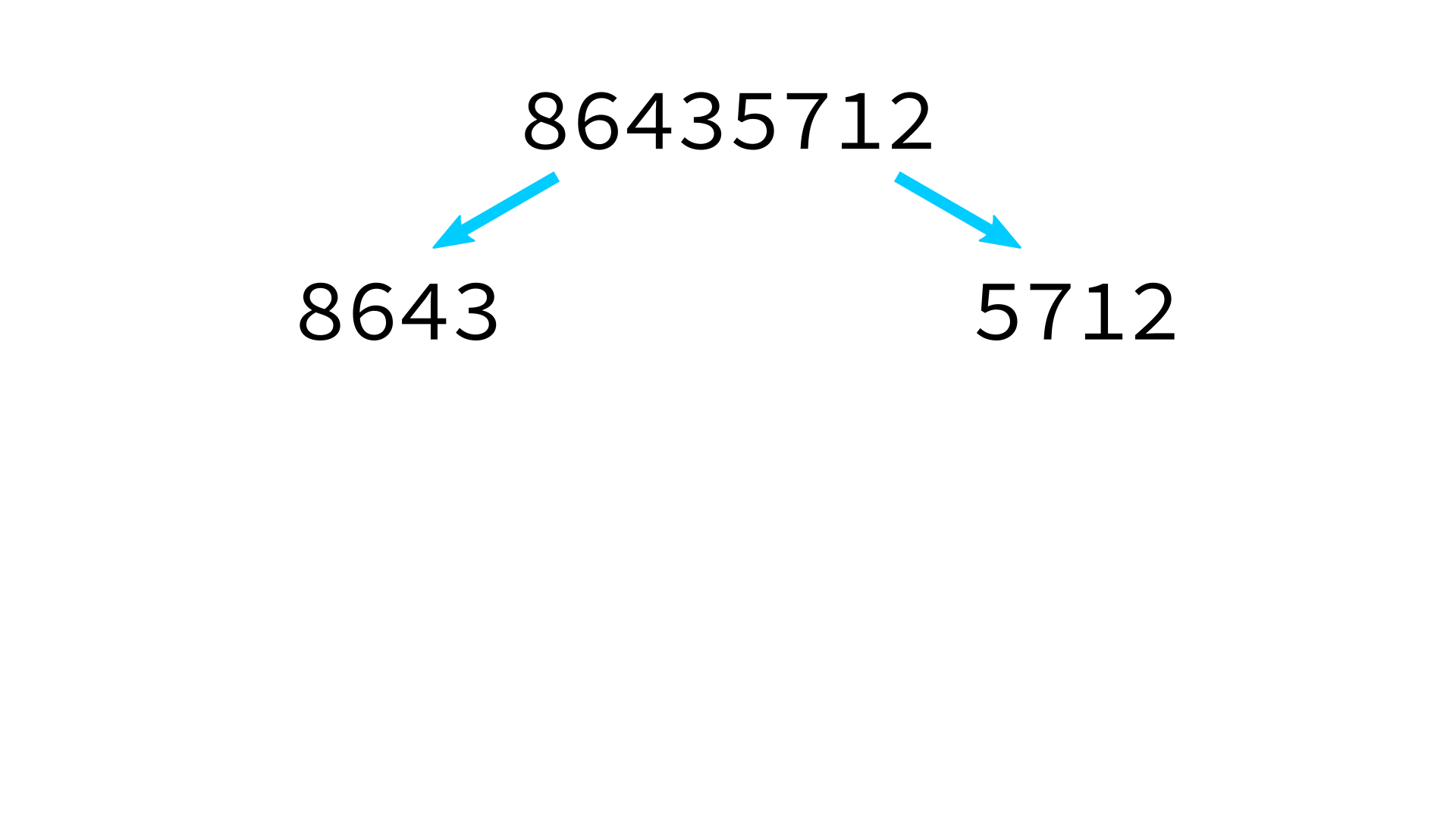
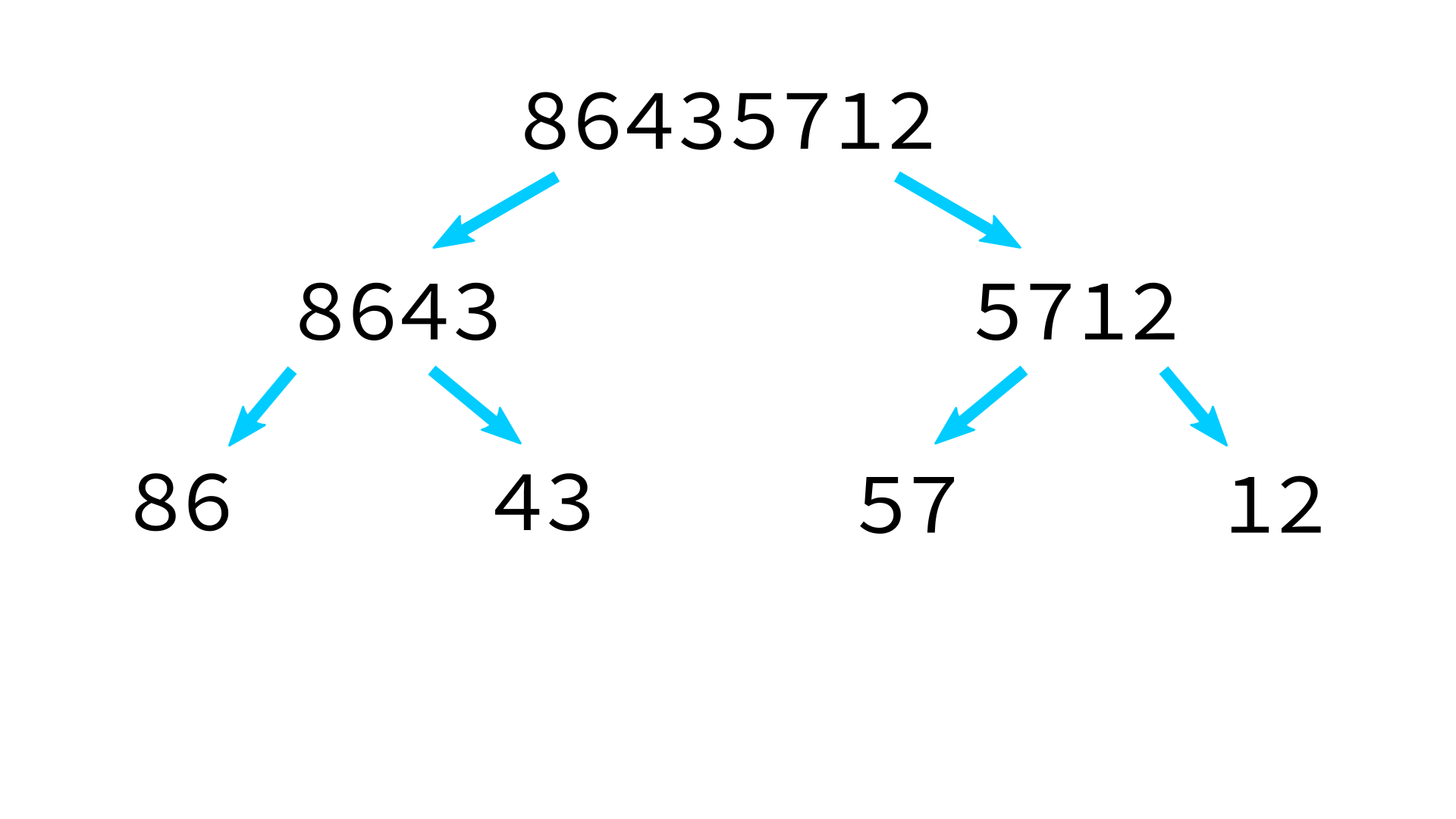
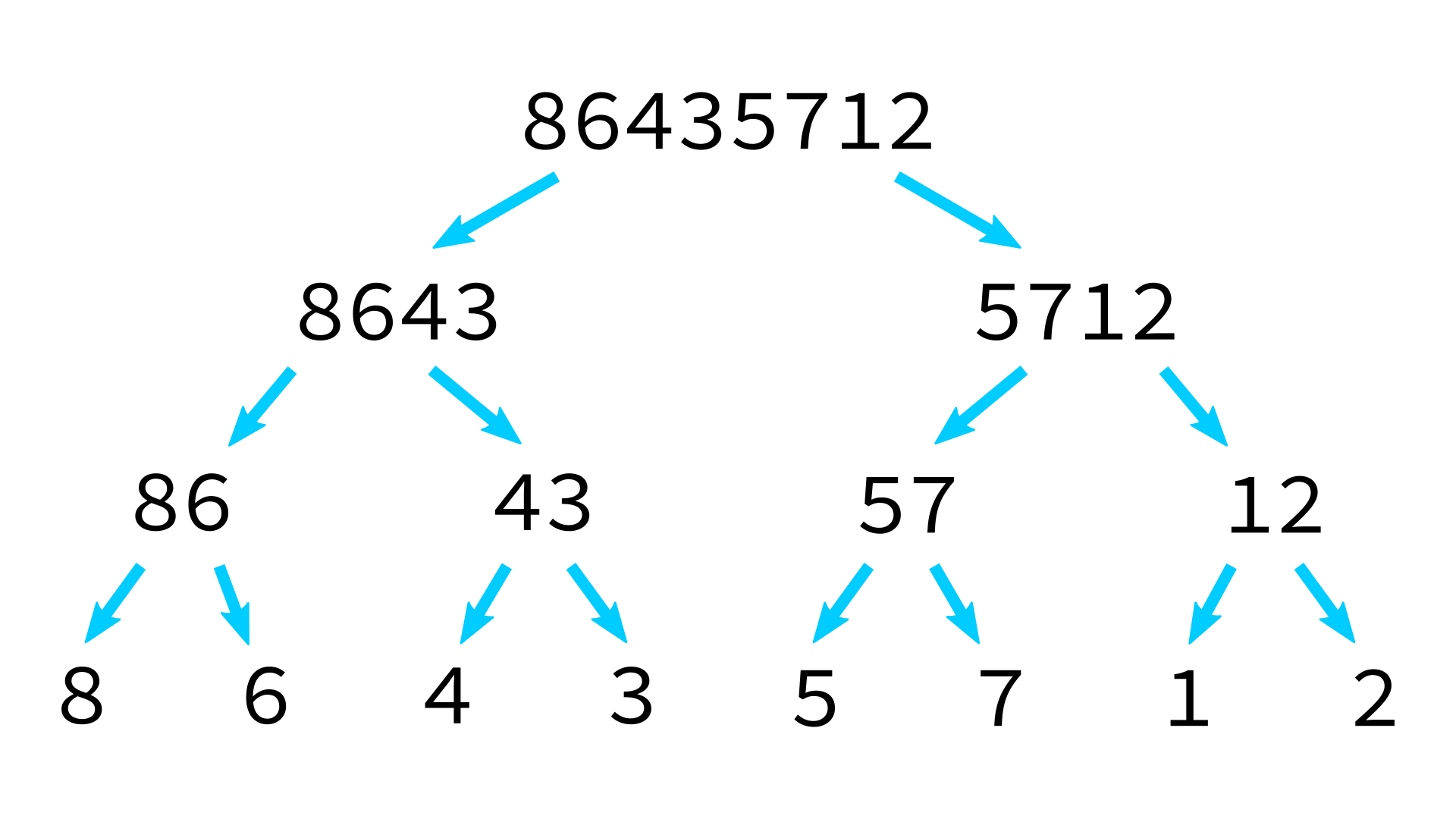
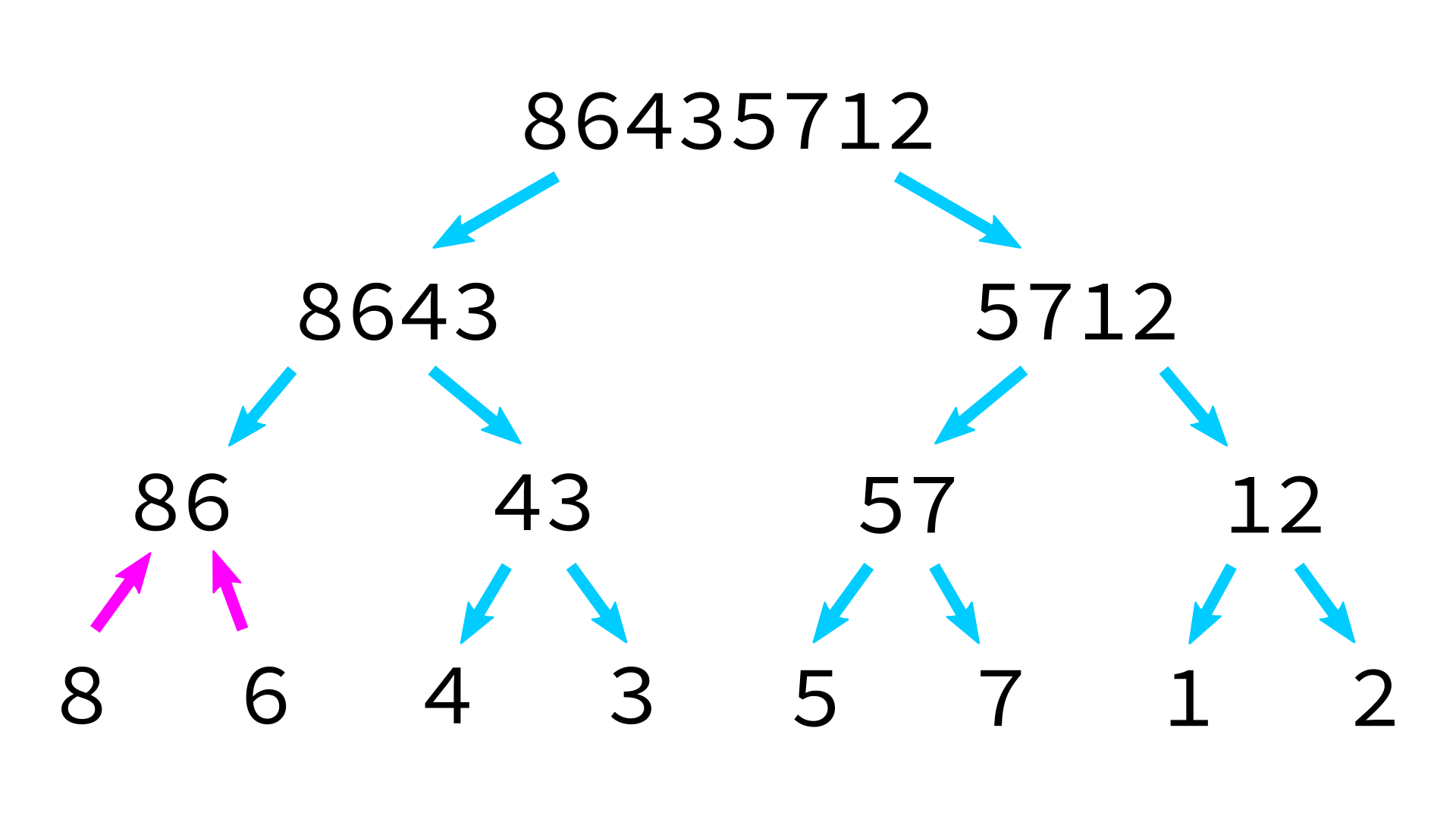
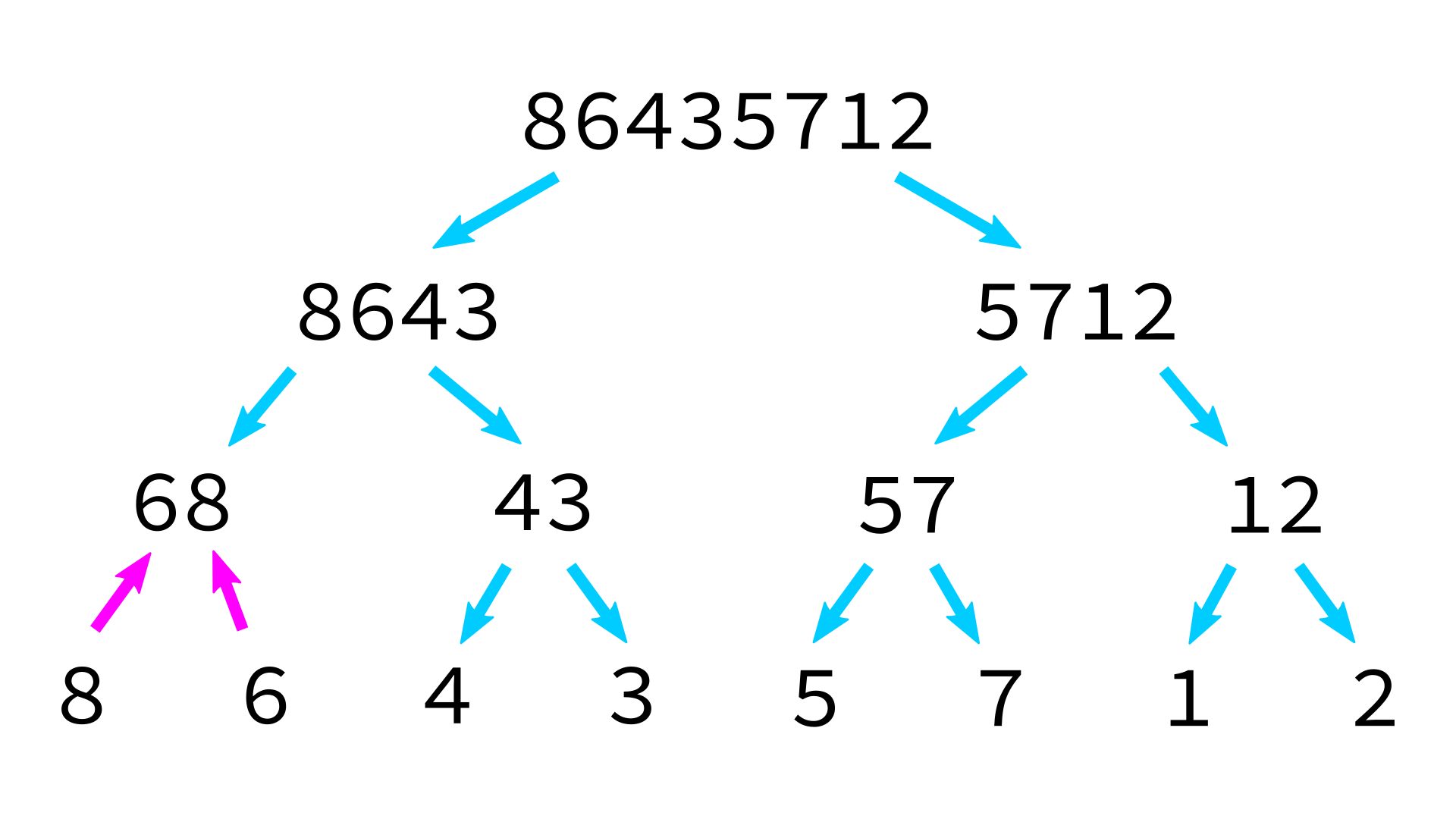
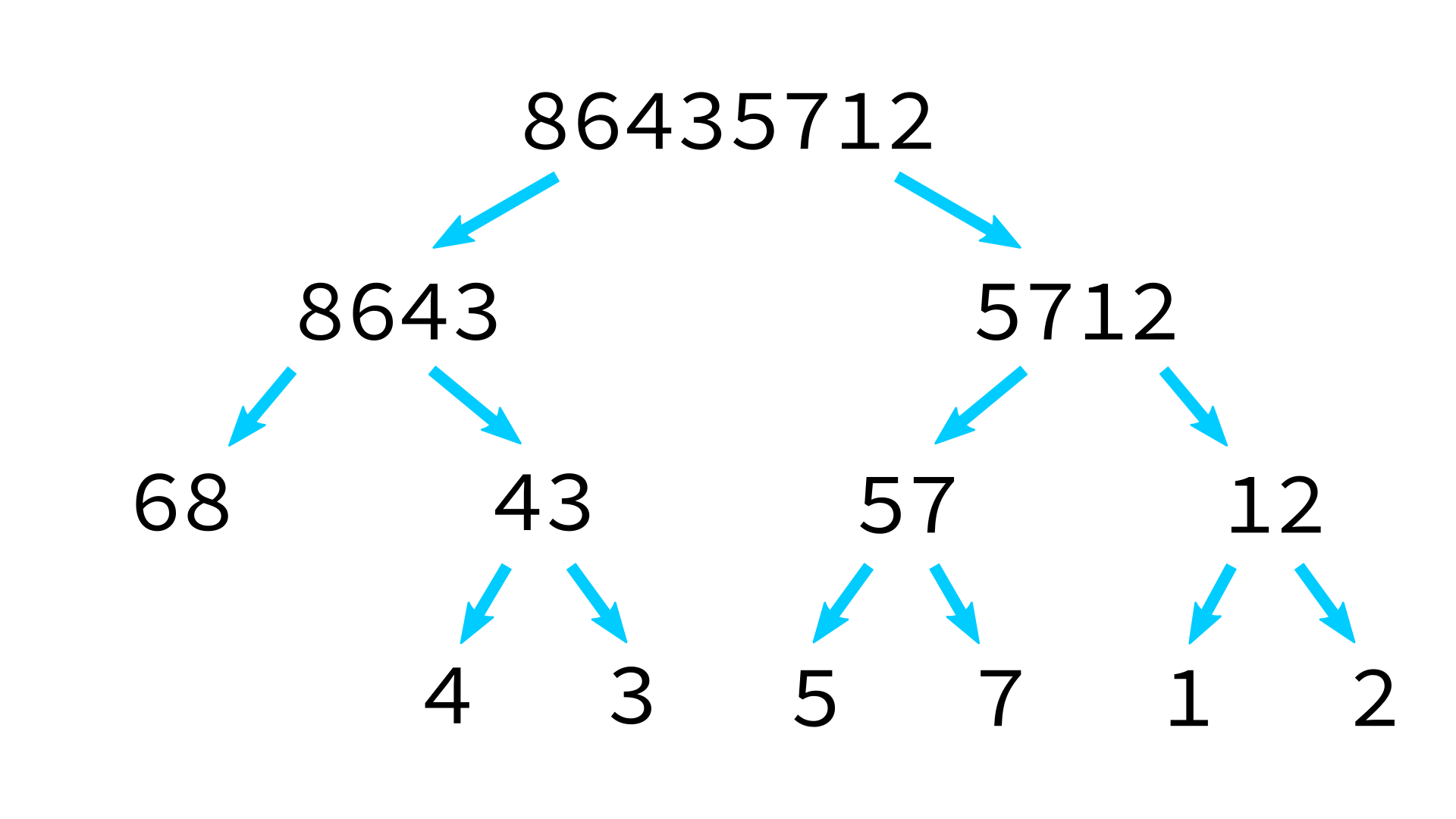
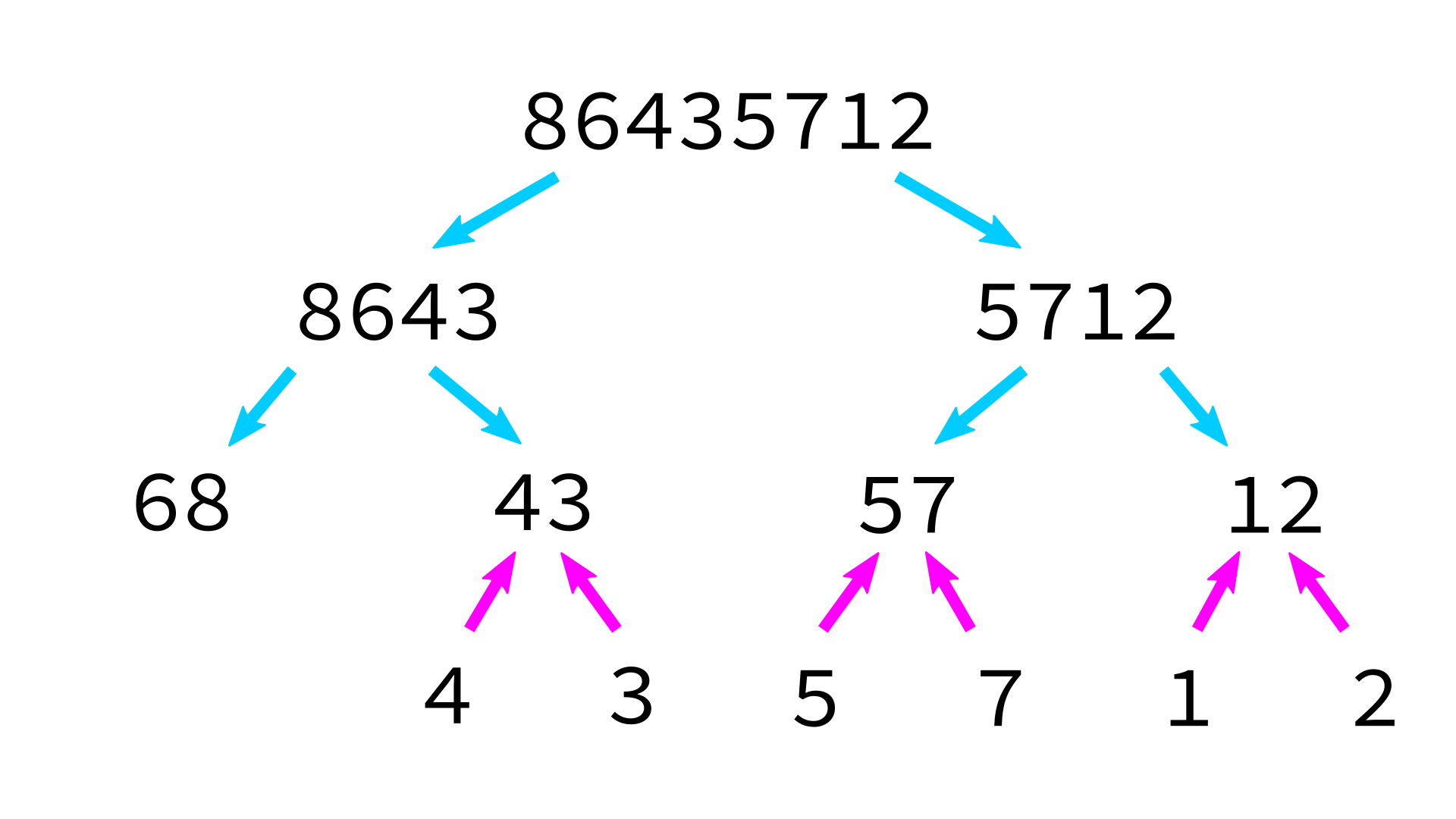
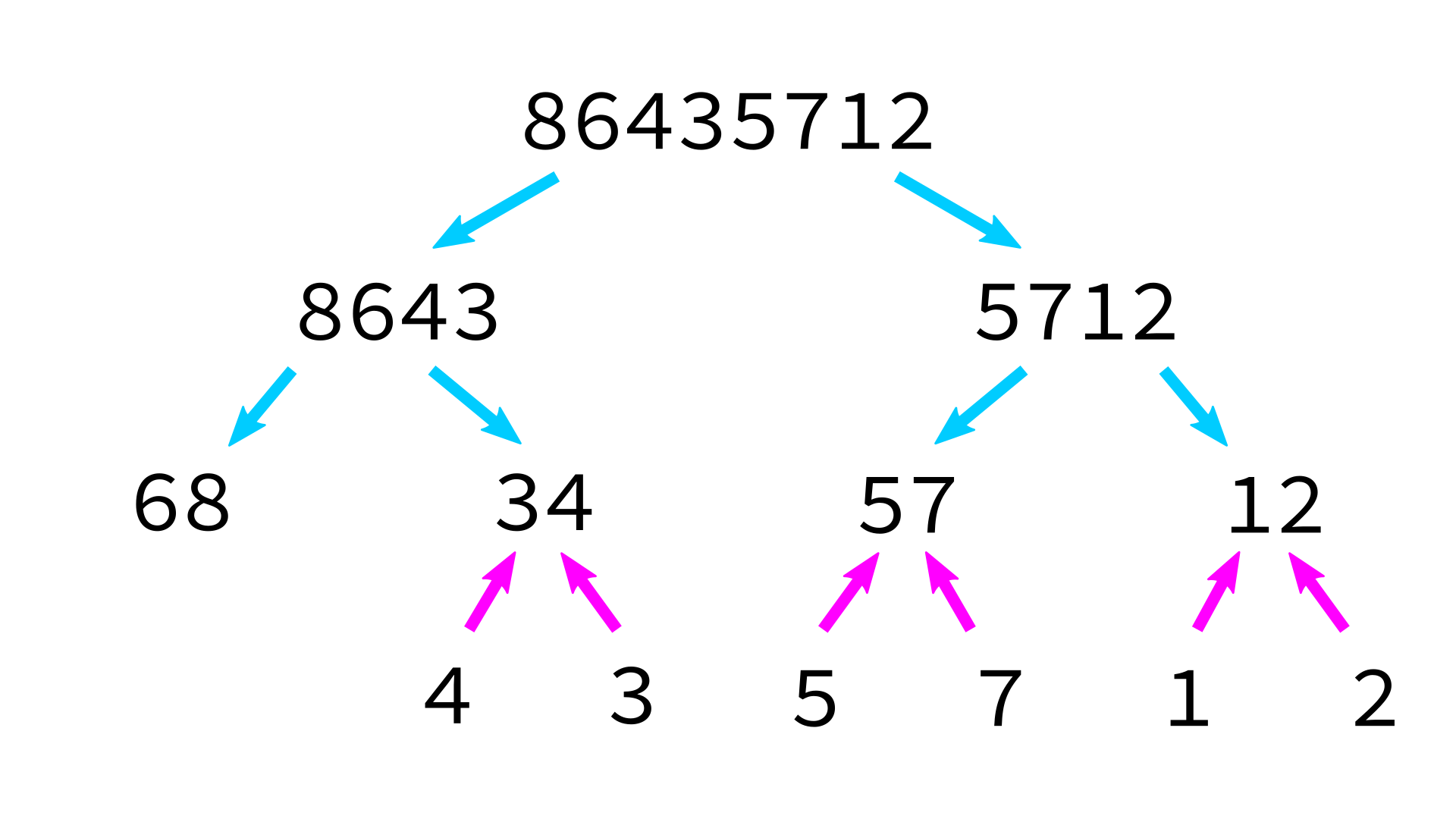
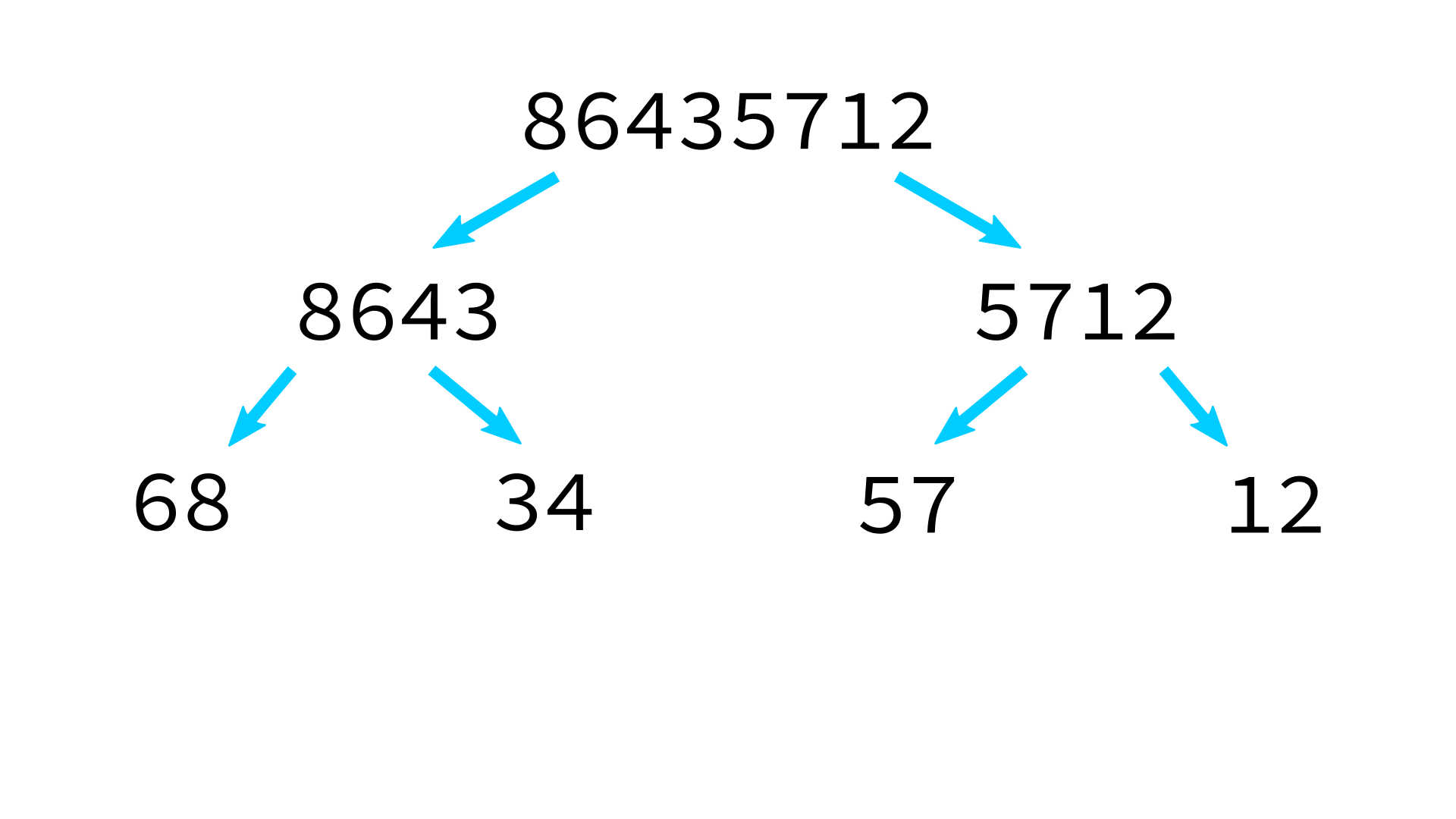
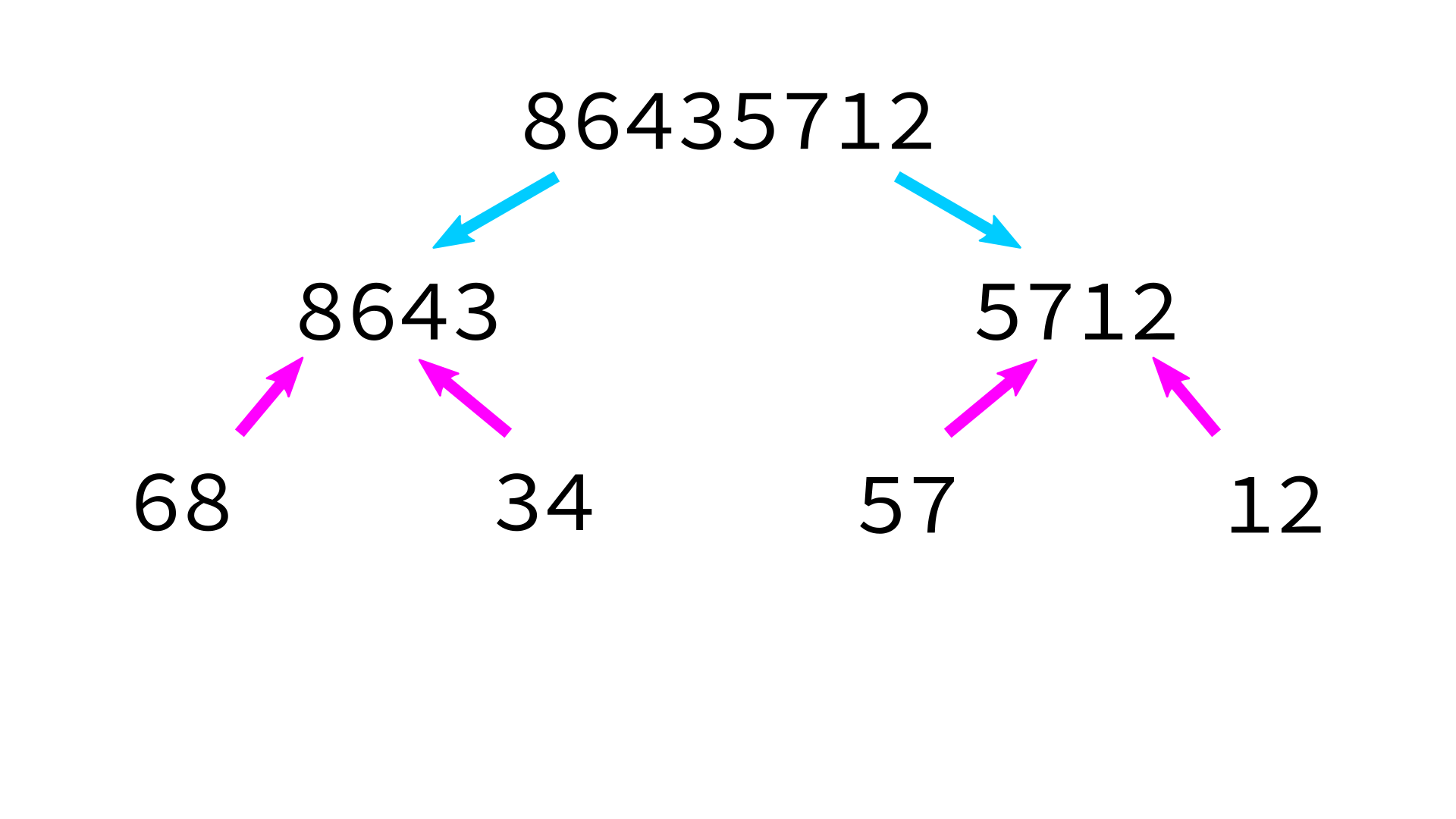
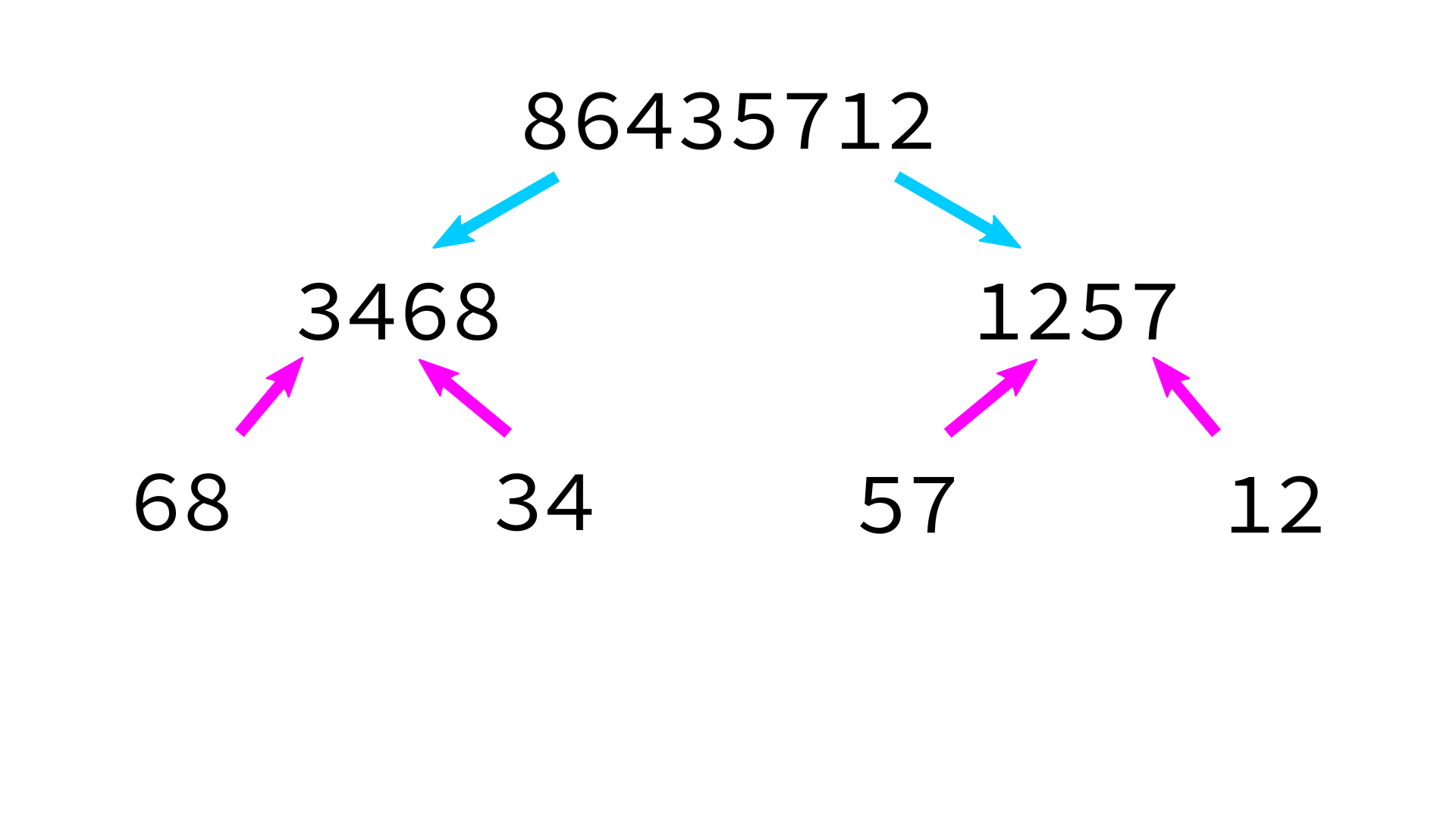
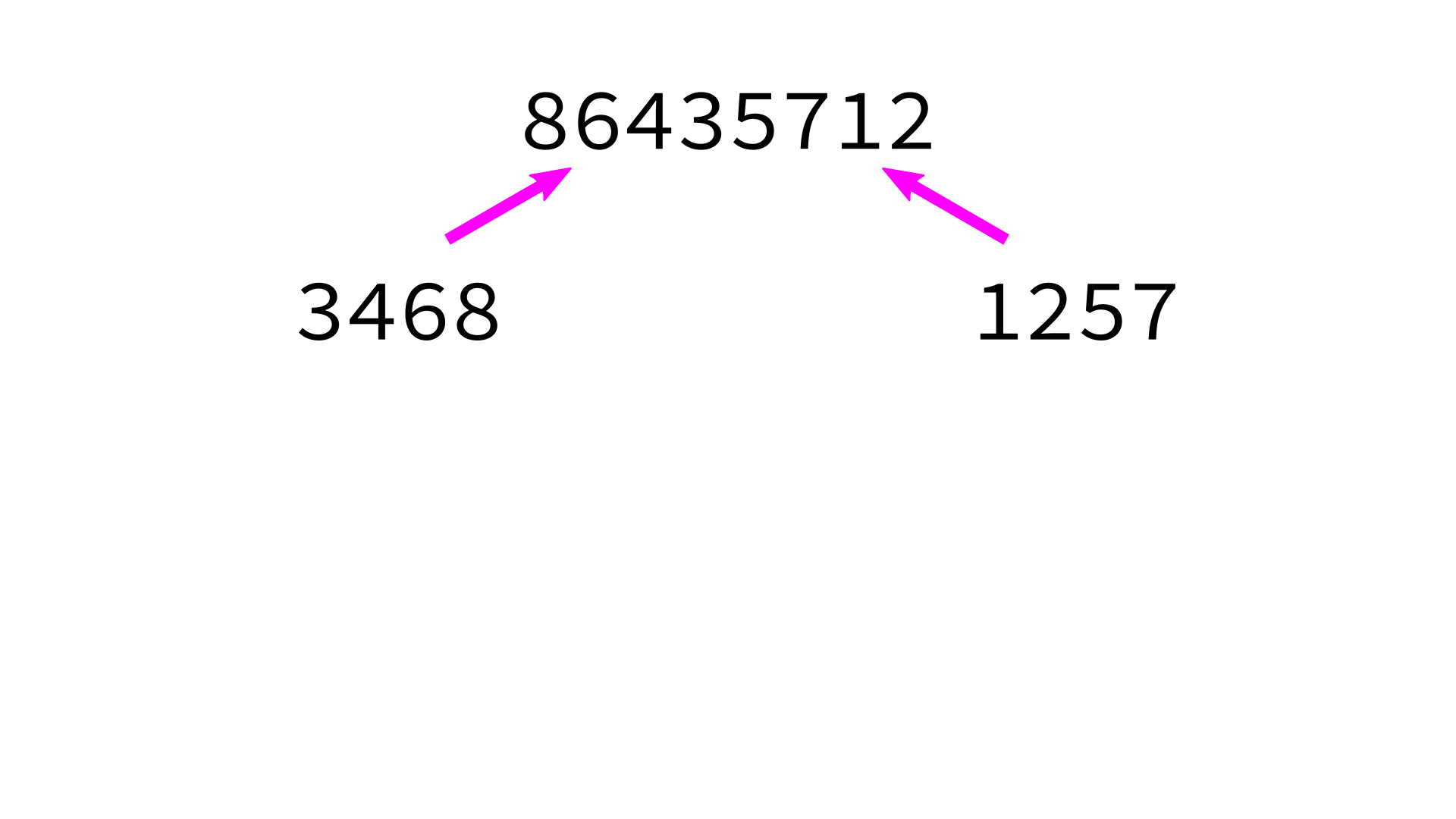
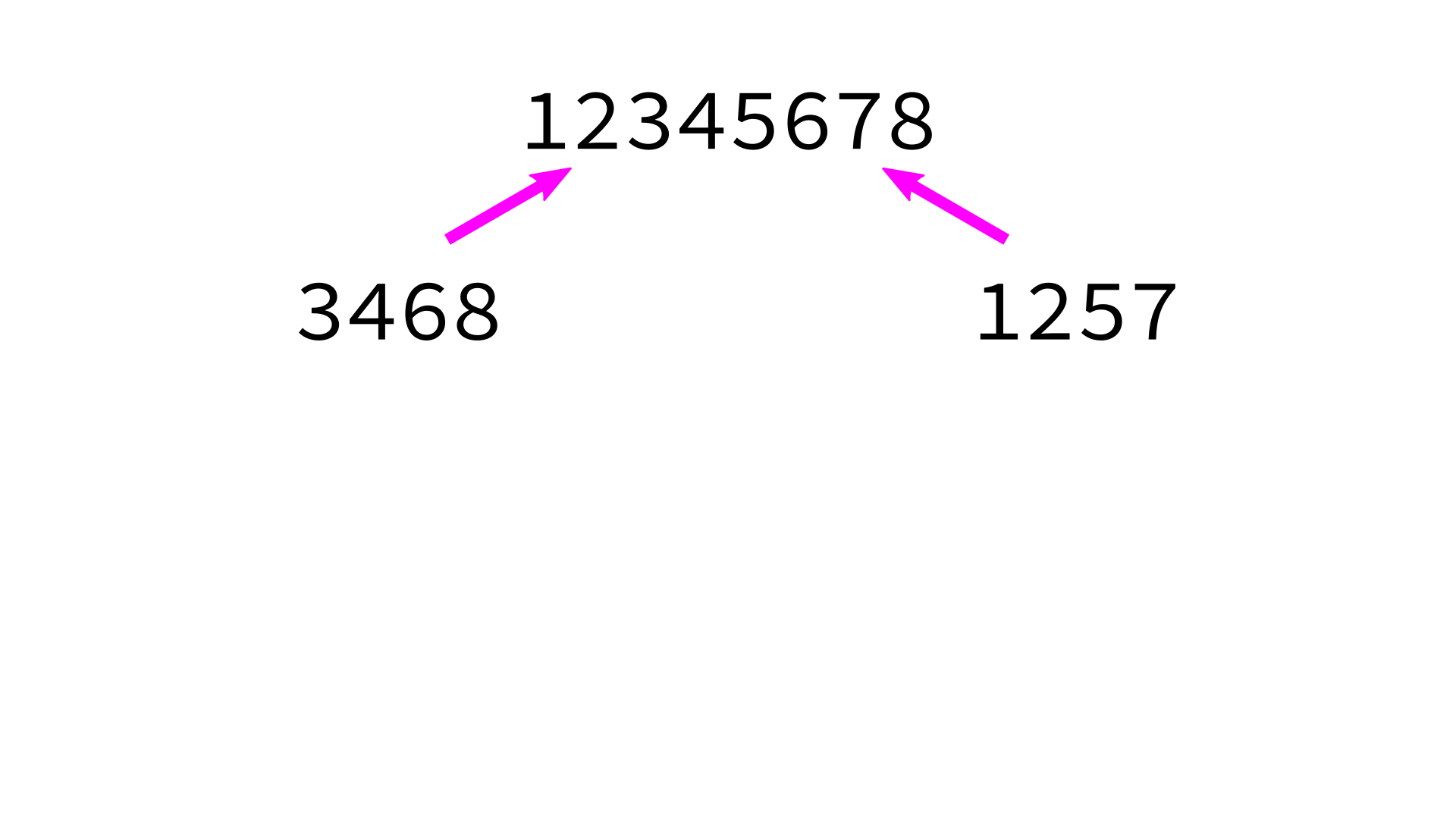
But how to merge?

This algorithm depends on having a function merge that can merge two sorted lists into a single sorted list.

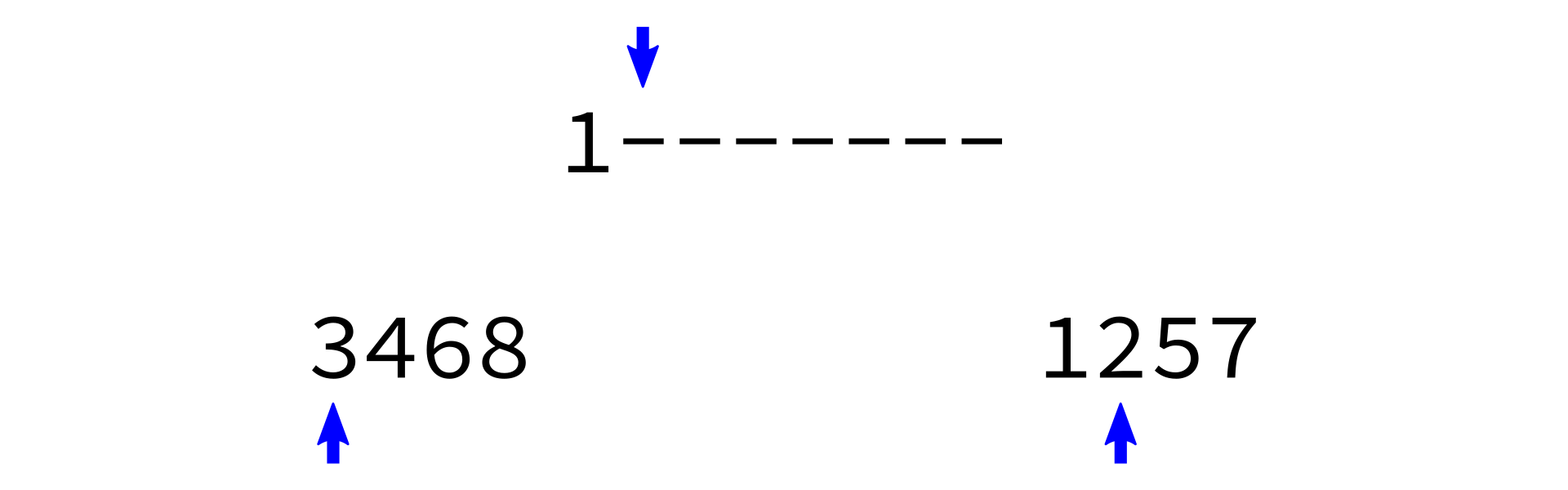
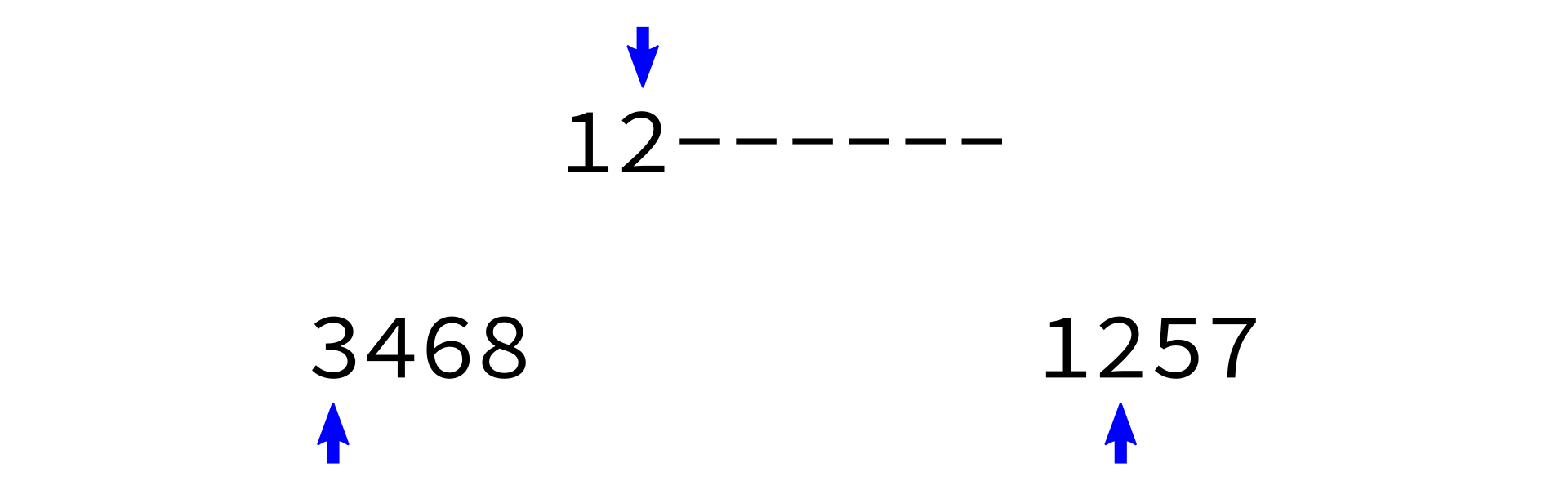
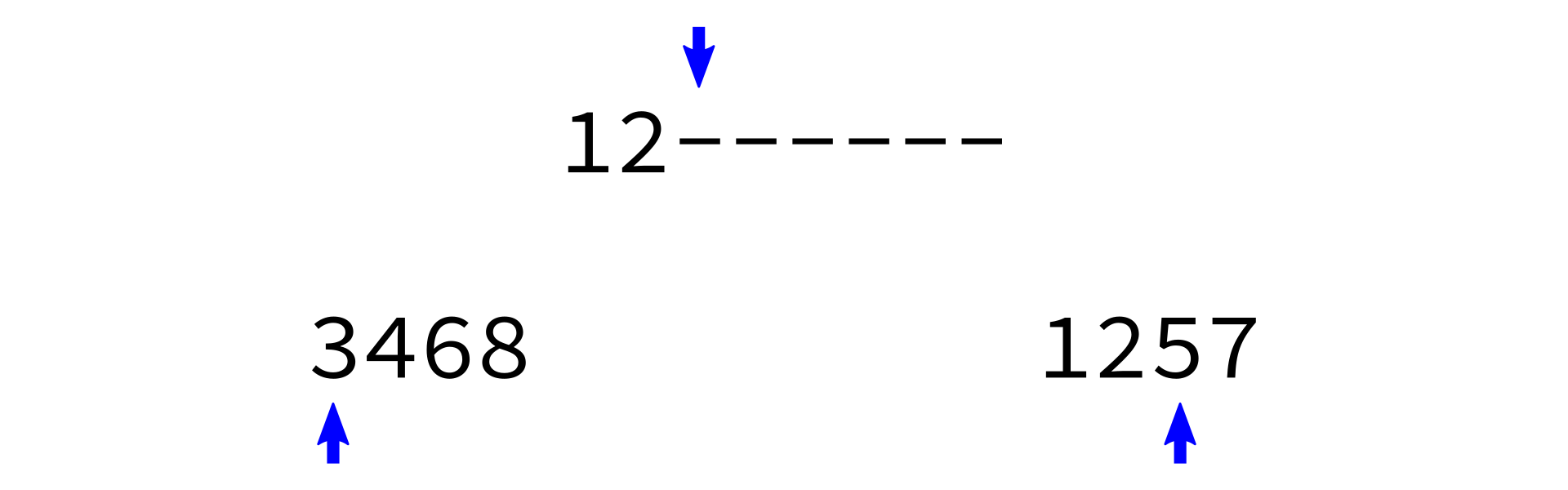
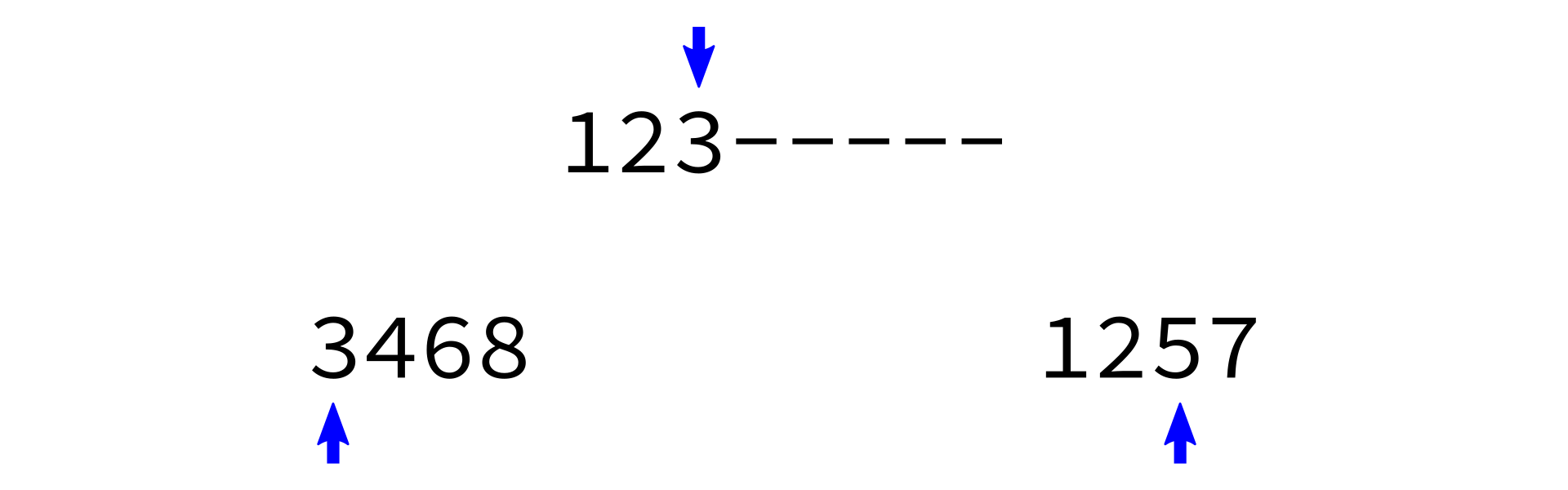
Algorithm merge:

Input: sorted lists L0 and L1.

Goal: return a sorted list with same items as L0+L1

  1. Make a new empty list L
  2. Make integer variables i0,i1 to keep track of current position in L0,L1 respectively. Set to zero.
  3. While i0 < len(L0) and i1 < len(L1), do the following:
    • Check which of L0[i0] and L1[i1] is smaller.
    • Append the smaller one to L.
    • Increment whichever one of i0,i1 was used.
  4. Append any remaining portion of L0 to L.
  5. Append any remaining portion of L1 to L.

Merging sorted lists

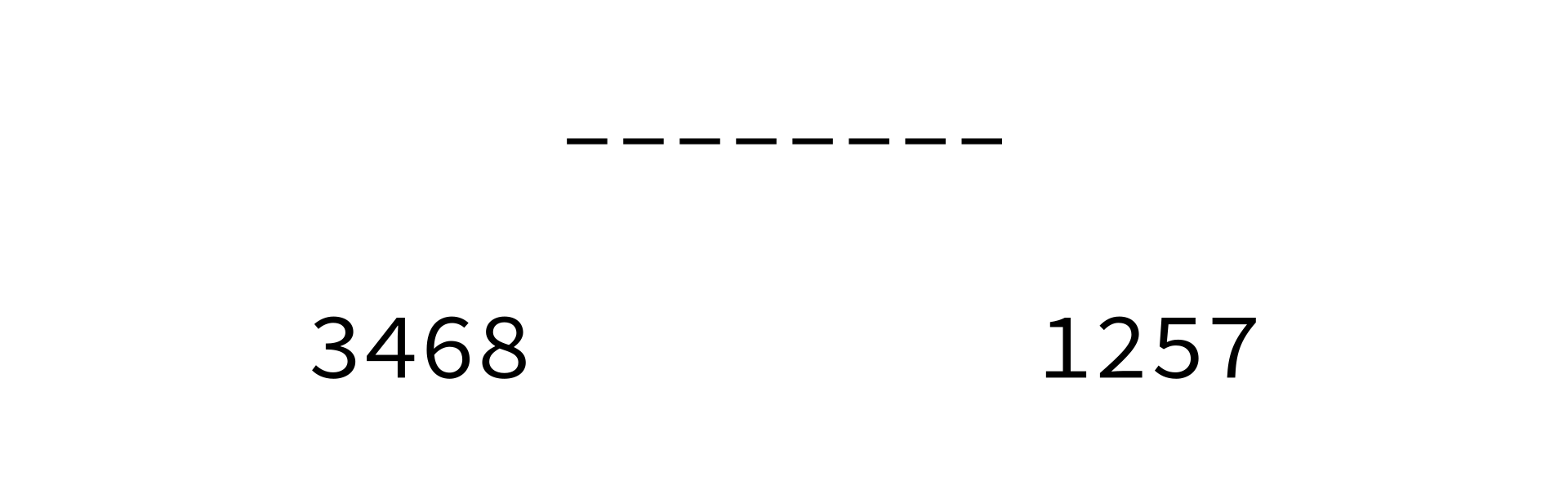
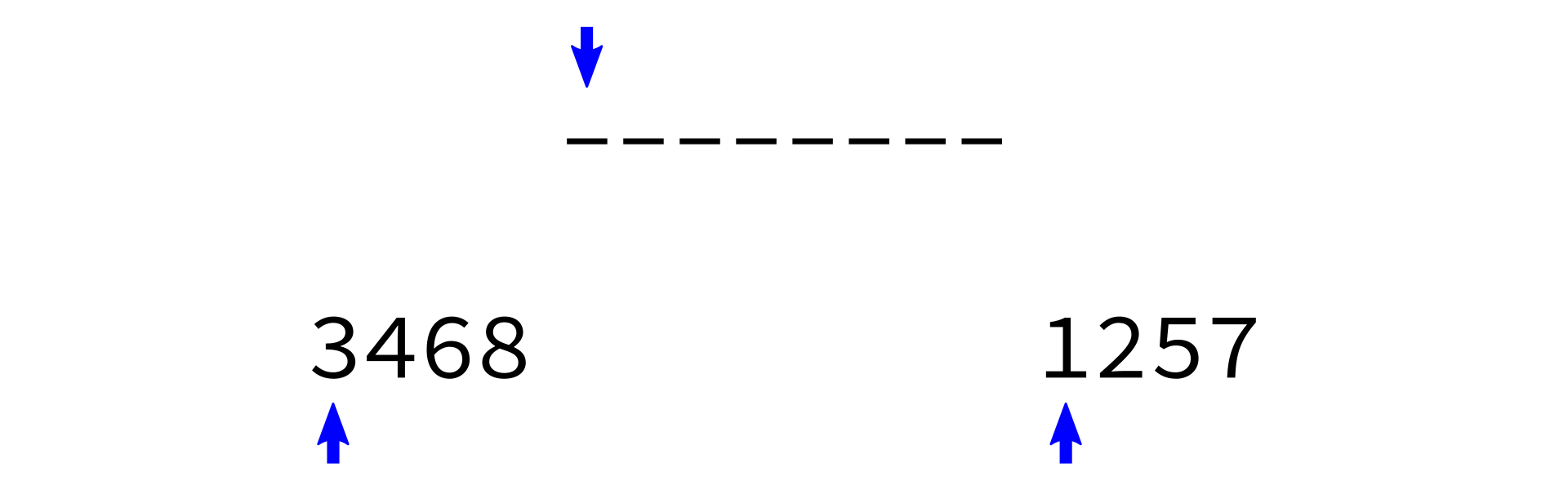
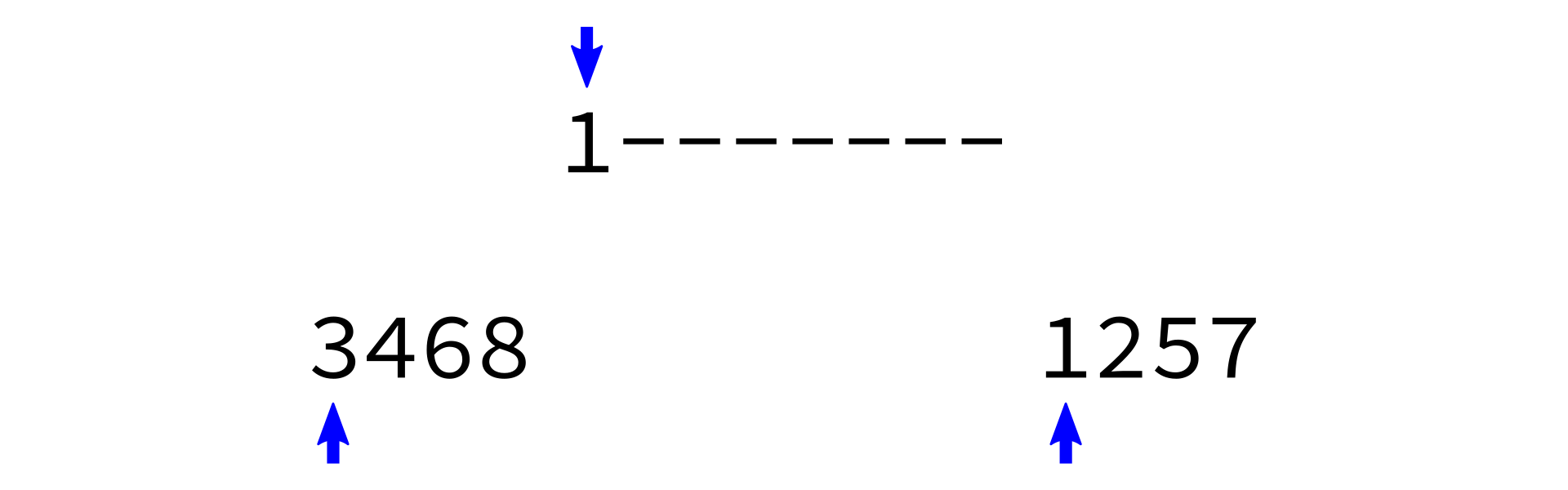
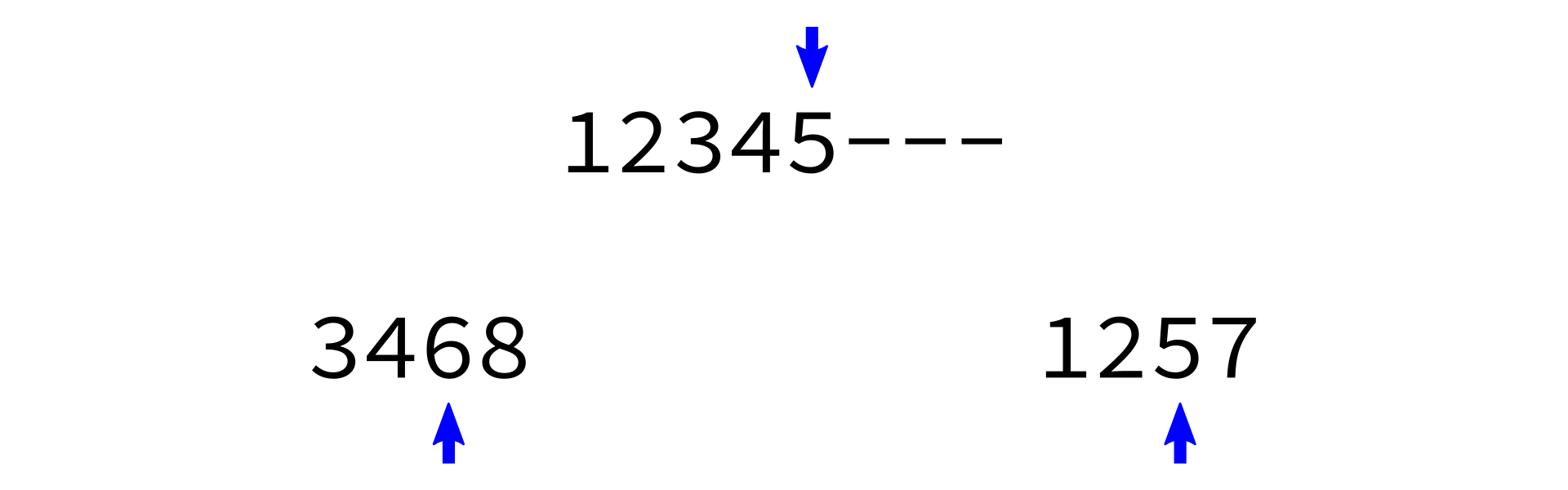
Coding time

Let's implement mergesort in Python.

References