Lecture 13
Recursion vs Iteration
MCS 275 Spring 2021
Emily Dumas
Lecture 13: Recursion vs Iteration
Course bulletins:
- Please complete anonymous feedback survey (link in Blackboard announcement)
- Project 1 grades and solutions posted
- Project 2 will be posted by Friday; due Feb 26
Loose end
Let's implement the paper folding sequence recursively.
Cool fact
If you use the infinite paper folding sequence as the binary digits of a real number (starting at $\frac{1}{2}$ place and moving right), you get the paper folding constant.
$$ \begin{split} PFC &= (0.11011001110010011101100\ldots)_2\\ &= 0.85073618820186\ldots \end{split} $$It is irrational. In 2007 it was shown1 that this constant is furthermore transcendental, i.e. cannot be expressed in terms of square roots, cube roots, or any solutions of polynomials with rational coefficients.
Stack overflow
Recursive functions are limited by a maximum call stack size.
Python imposes a limit to prevent the memory area used to store the call stack from running out (a stack overflow), which would abruptly stop the interpreter.
Iterative solutions
Let's write iterative versions of factorial, Fibonacci, and paper folding. (Or as many as time allows.)
Timing comparison
How do iterative and recursive versions compare on speed?
I made a module decs contains a decorator called timed that prints the time a function takes to return.
Question
Why is recursive fact() somewhat competitive, but fib() is dreadfully slow?
Decorator decs.count_calls will keep track of number of function calls.
fact call graph



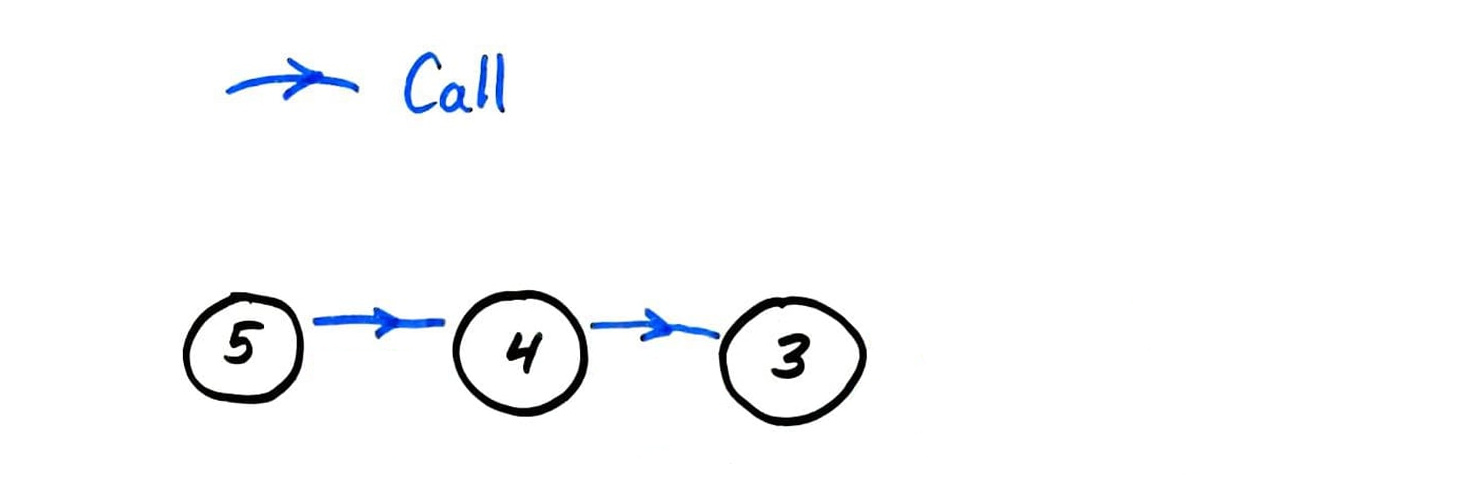
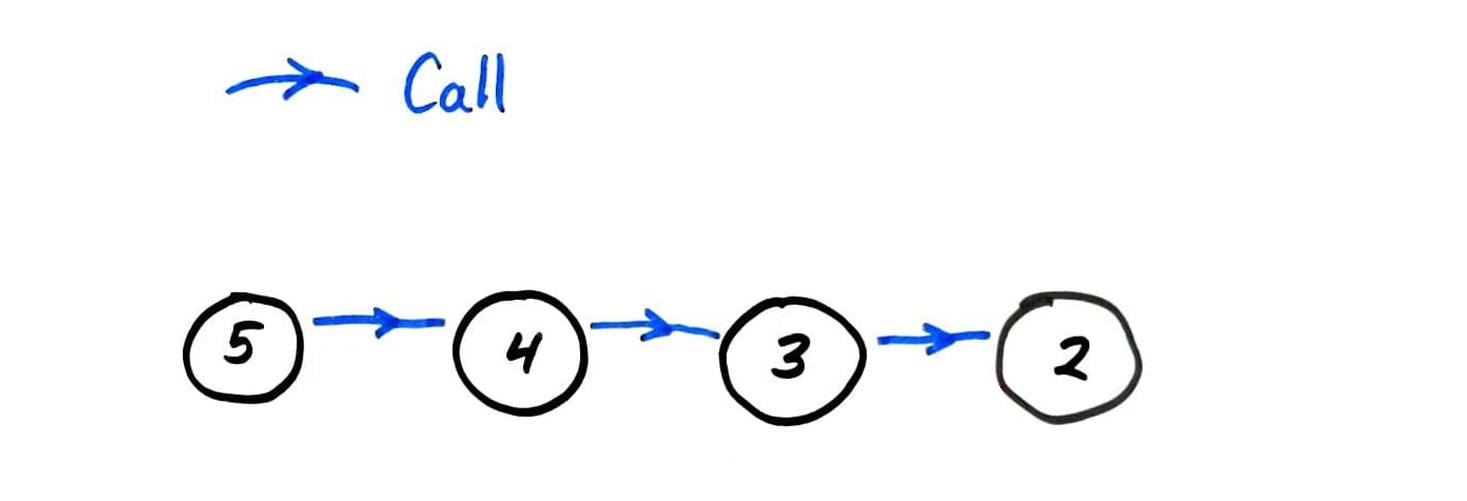

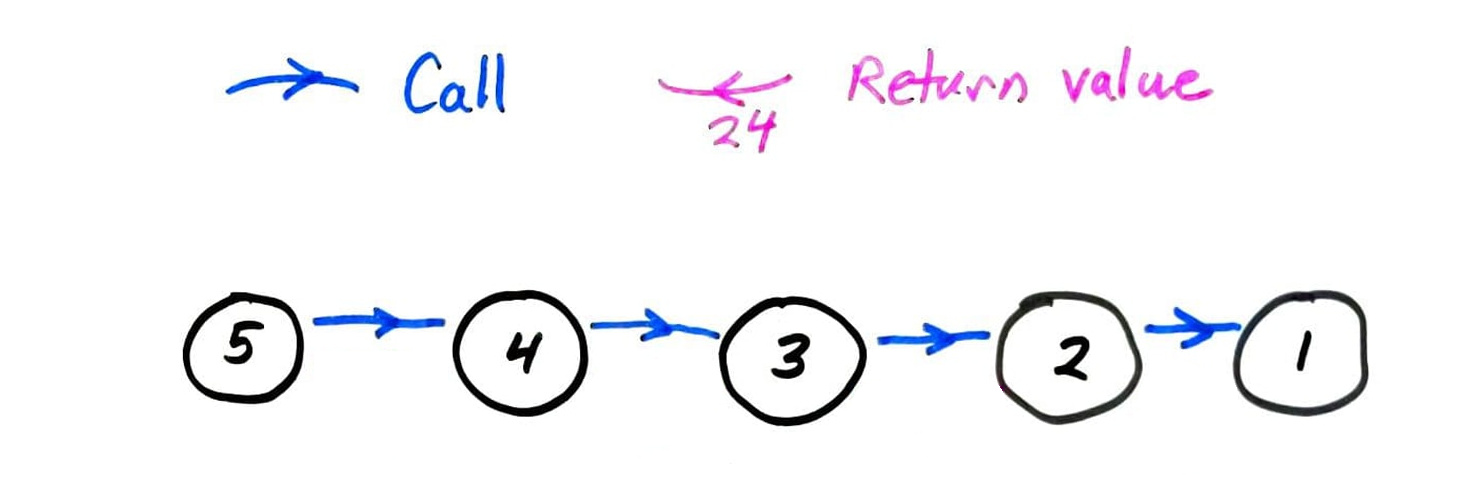
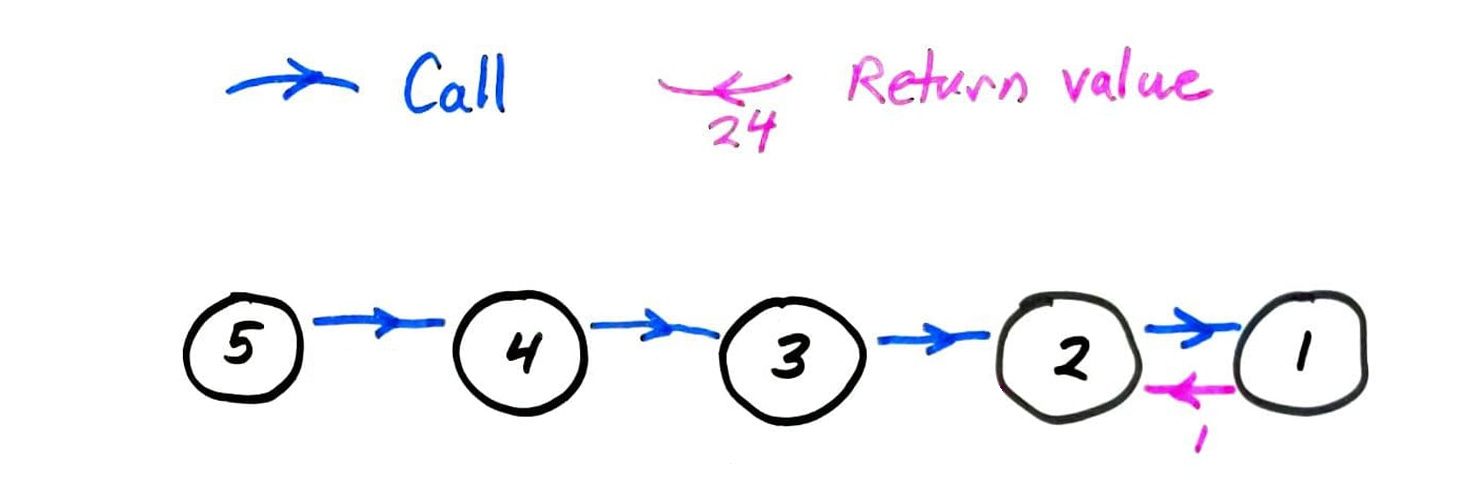
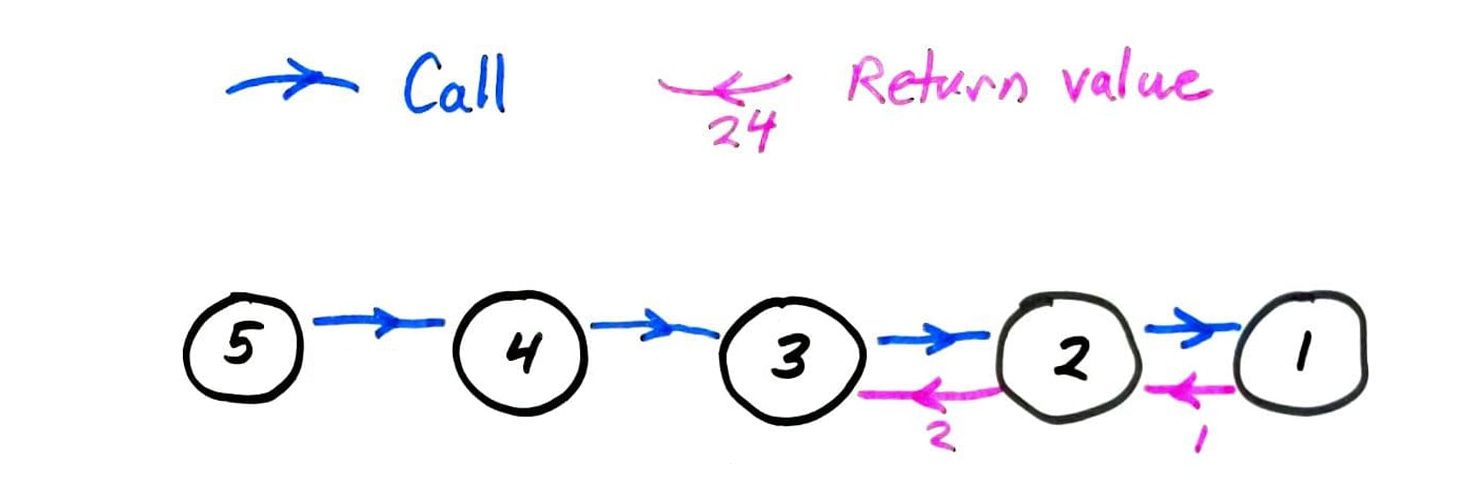


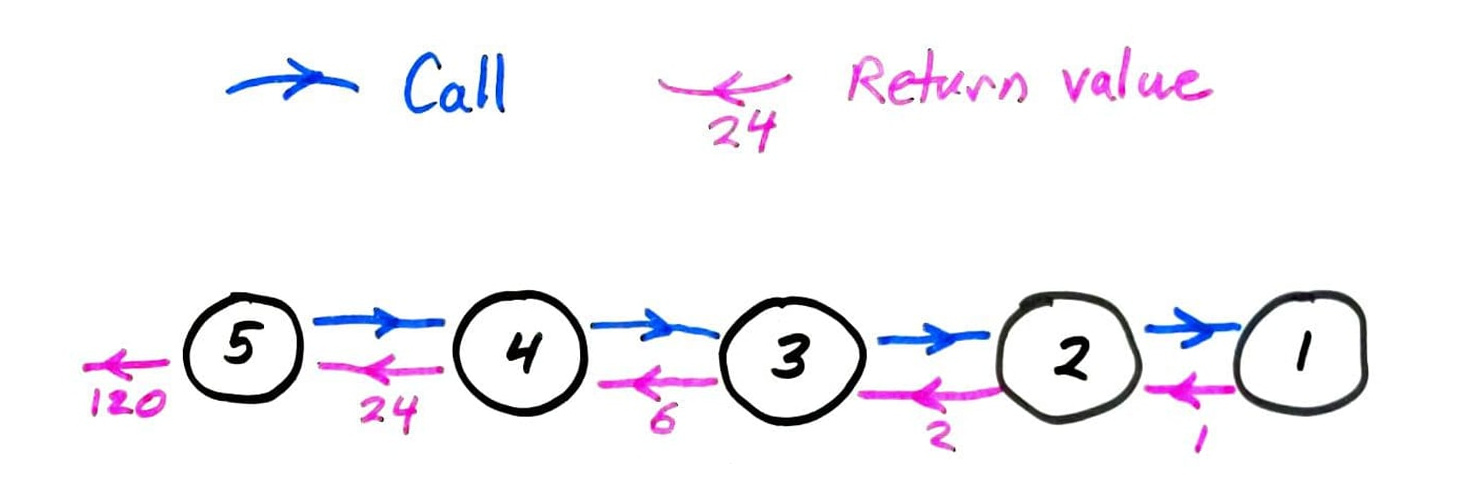
fib call graph

fib call graph

Memoization
fib computes the same terms over and over again.
Instead, let's store all previously computed results, and use the stored ones whenever possible.
This is called memoization. It only works for pure functions, i.e. those which always produce the same return value for any given argument values.
math.sin(...) is pure; time.time() is not.
memoized fib call graph

memoized fib call graph

Fibonacci timing summary
| n=35 | n=450 | |
|---|---|---|
| recursive | 1.9s | > age of universe |
| memoized recursive | <0.001s | 0.003s |
| iterative | <0.001s | 0.001s |
Measured on a 4.00Ghz Intel i7-6700K CPU (2015 release date) with Python 3.8.5
Memoization summary
Recursive functions with multiple self-calls often benefit from memoization.
Memoized version is conceptually similar to an iterative solution.
Memoization does not alleviate recursion depth limits.
References
- Algorithms by Jeff Erickson, available as a free PDF, discusses some examples of recursion in Chapter 1.
- Lutz discusses recursive functions in Chapter 19 (pages 555-559 in the print edition).
- Intro to Python for Computer Science and Data Science by Deitel and Deitel discusses recursion in Chapter 11. The online version of this text is freely available to UIC students, faculty, and staff. (You will first need to log in with you UIC email.)
- The open textbook Think Python, 2ed, by Allen B. Downey discusses recursion in Sections 5.8 to 5.10.
- Computer Science: An Overview by Brookshear and Brylow discusses recursion in Section 5.5. (This book is often an optional text for MCS 260.)
Revision history
- 2021-02-10 Add reference for transcendence of $PFC$
- 2021-02-10 Initial publication