Lecture 17
Quicksort
MCS 275 Spring 2021
Emily Dumas
Lecture 17: Quicksort
Course bulletins:
- Starting with Quiz 6, you will have 48 hours for quizzes (Noon Sunday to Noon Tuesday).
- Project 2 description updated with sample data and modules policy.
- Project 2 due 6pm CST Friday, February 26.
- Check out the recursion sample code.
- Worksheet 7 will explore recursive maze solver / generator in more depth.
Plan
- Discuss mergesort a bit more
- Introduce quicksort
- Implement quicksort
Why discuss algorithms?
Python lists have built-in .sort() method. Why talk about sorting?
- Study cases of easy-to-explain problems solved in clever ways.
- See patterns of thinking that work in other settings.
Mergesort
Last time we discussed and implemented mergesort.
History: Developed by von Neumann (1945) and Goldstine (1947).
But is it a good way to sort a list?
Efficiency
Theorem: If you measure the time cost of mergesort in any of these terms
- Number of comparisons made
- Number of assignments (e.g.
L[i] = xcounts as 1) - Number of Python statements executed
then the cost to sort a list of length $n$ is less than $C n \log(n)$, for some constant $C$ that only depends on which expense measure you chose.
Asymptotically optimal
$C n \log(n)$ is pretty efficient for an operation that needs to look at all $n$ elements. It's not linear in $n$, but it only grows a little faster than linear functions.
Furthermore, $C n \log(n)$ is the best possible time for comparison sort of $n$ elements (though different methods might have better $C$).
Quicksort
Another comparison sort typically implemented using recursion. Developed by Hoare, 1959.
Unlike mergesort, it uses very little temporary storage, and only ever swaps pairs of elements.
Quicksort summary
Starting with an unsorted list:
- If the list has 0 or 1 elements, return immediately.
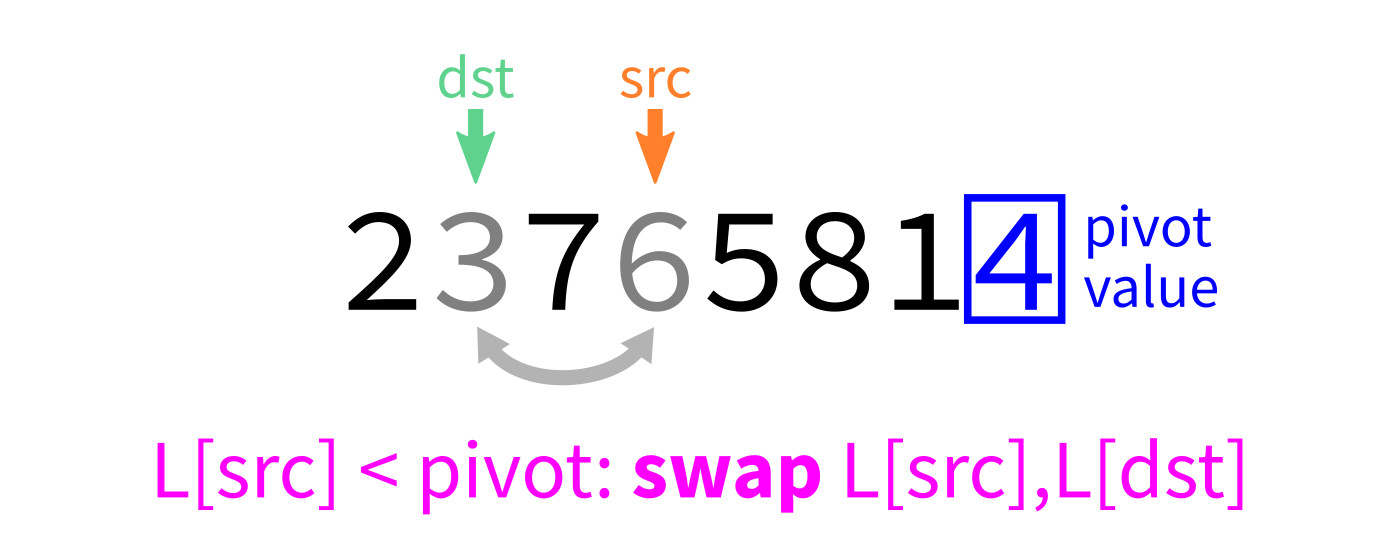
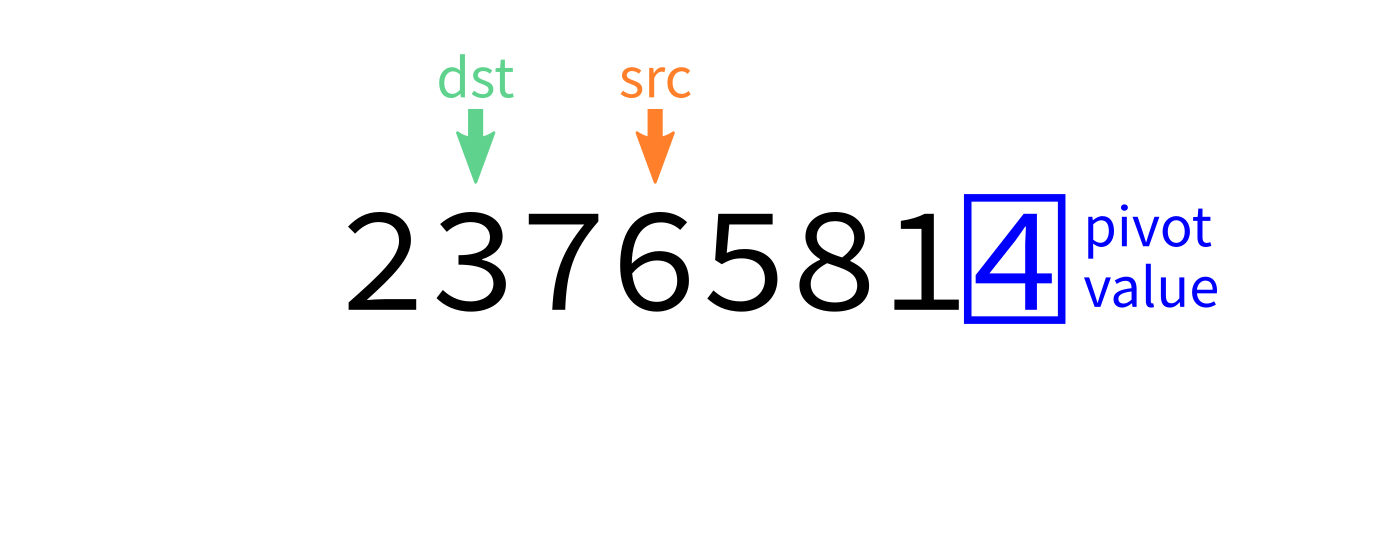
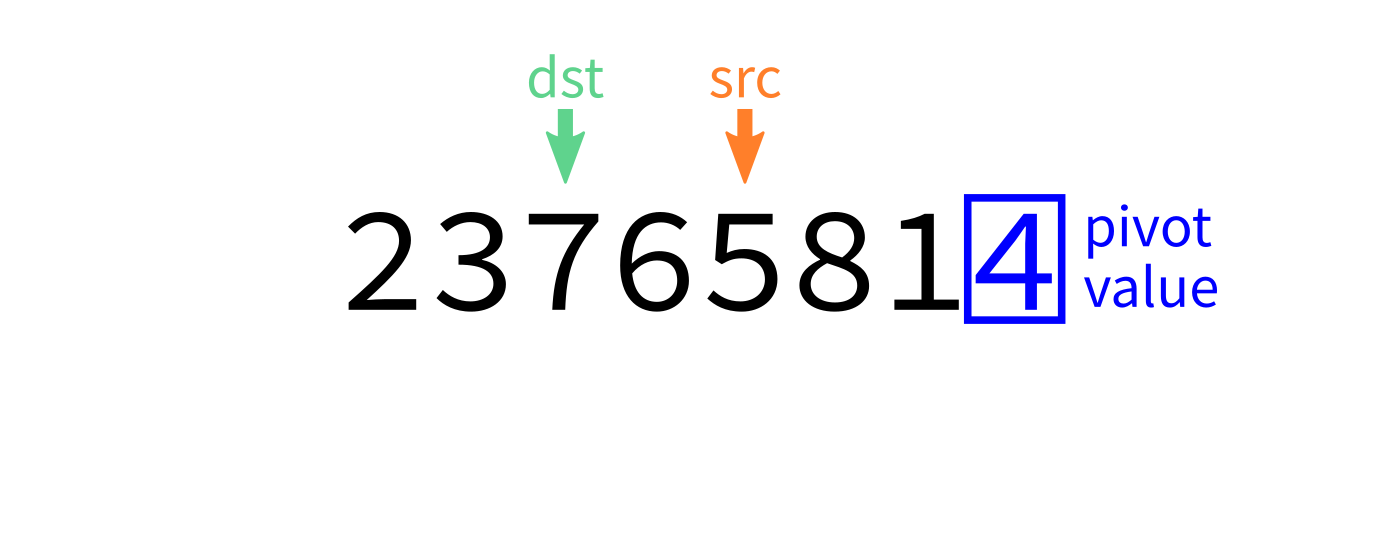
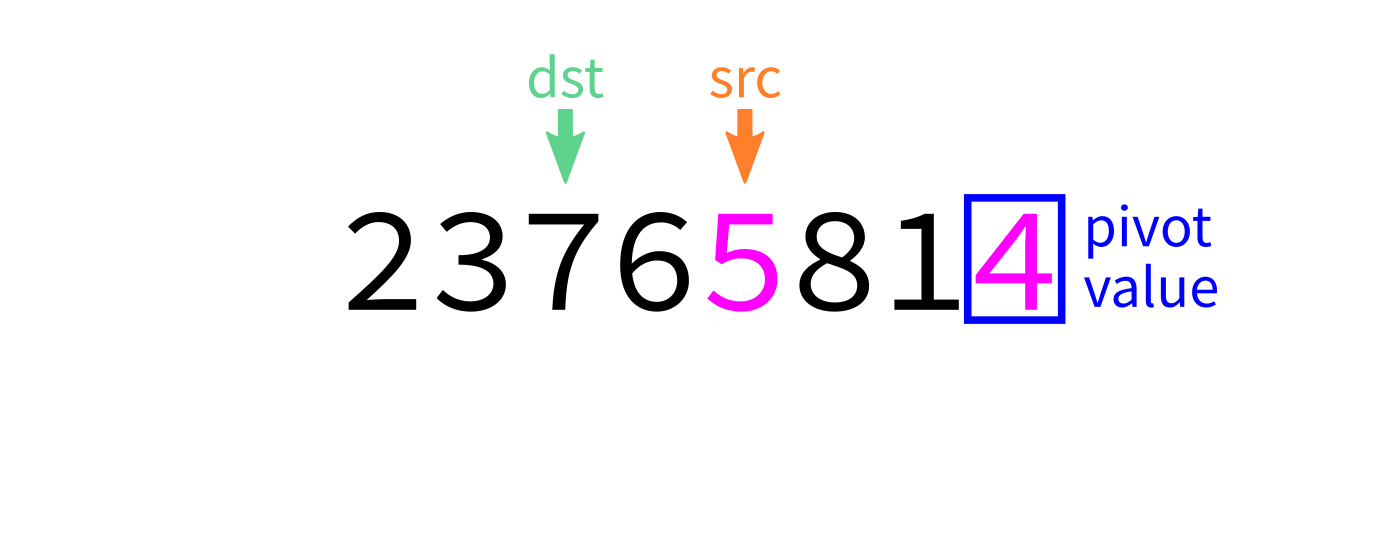
- Partition: Choose an element (the pivot). Rearrange so elements smaller than the pivot come before it, elements larger than the pivot come after it.
- Quicksort the part of the list before the pivot.
- Quicksort the part of the list after the pivot.
It's divide and conquer, but with no merge step. The hard work is instead in partitioning.
Quicksort visualization






























Assume we have partition
For the moment, we'll take the partition step as a "black box", assuming we already have:
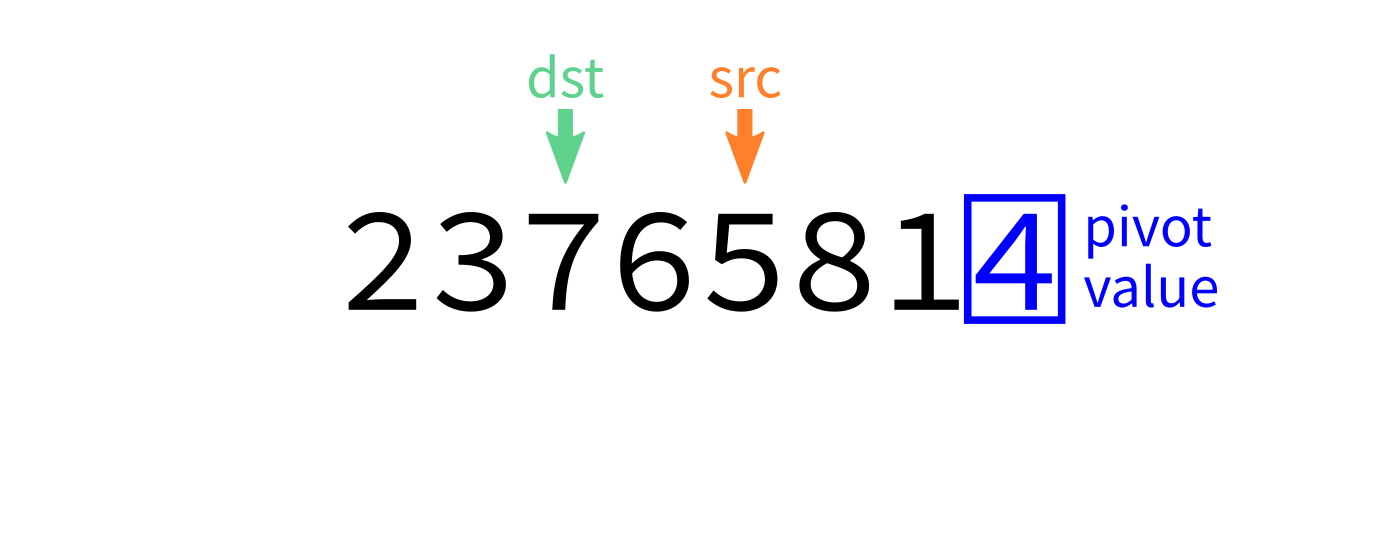
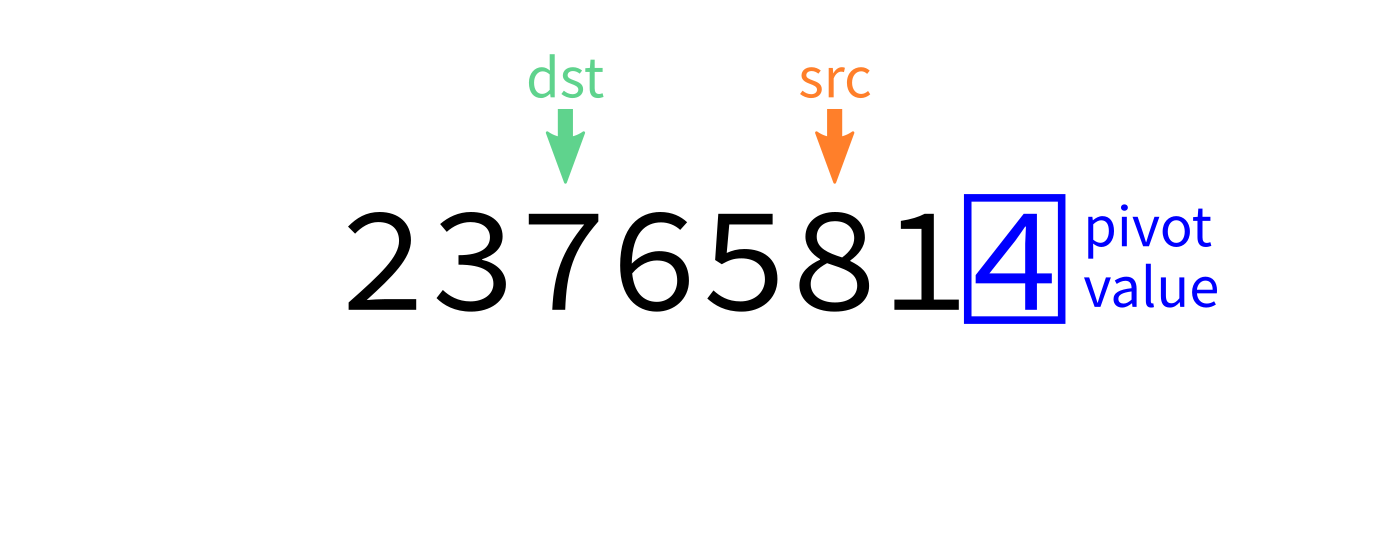
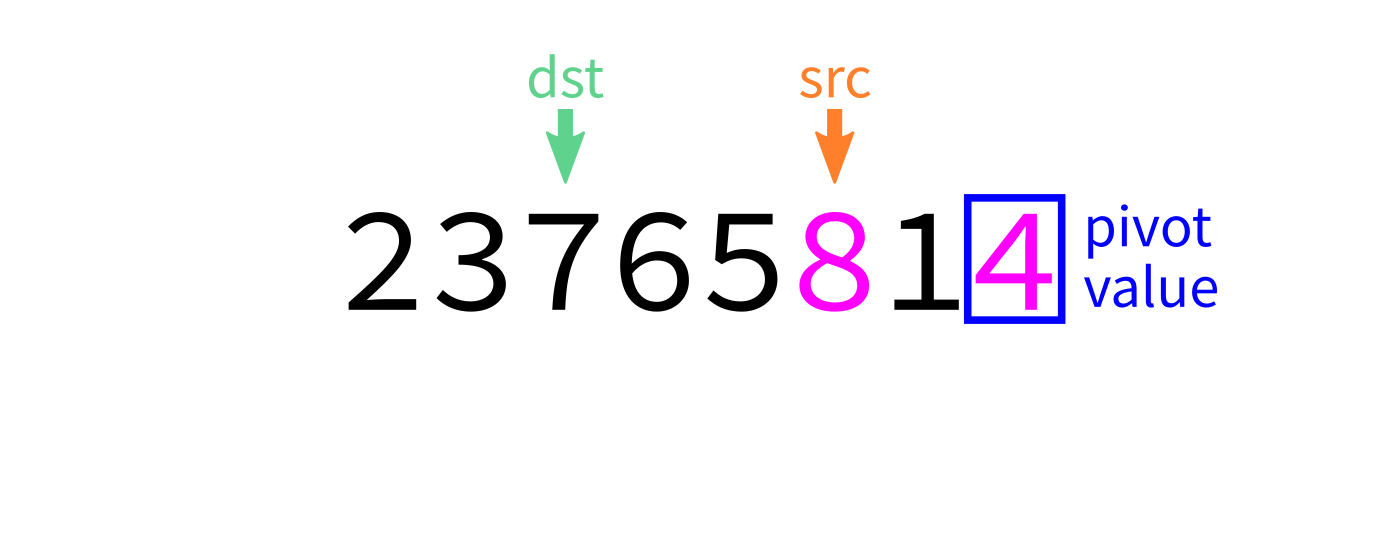
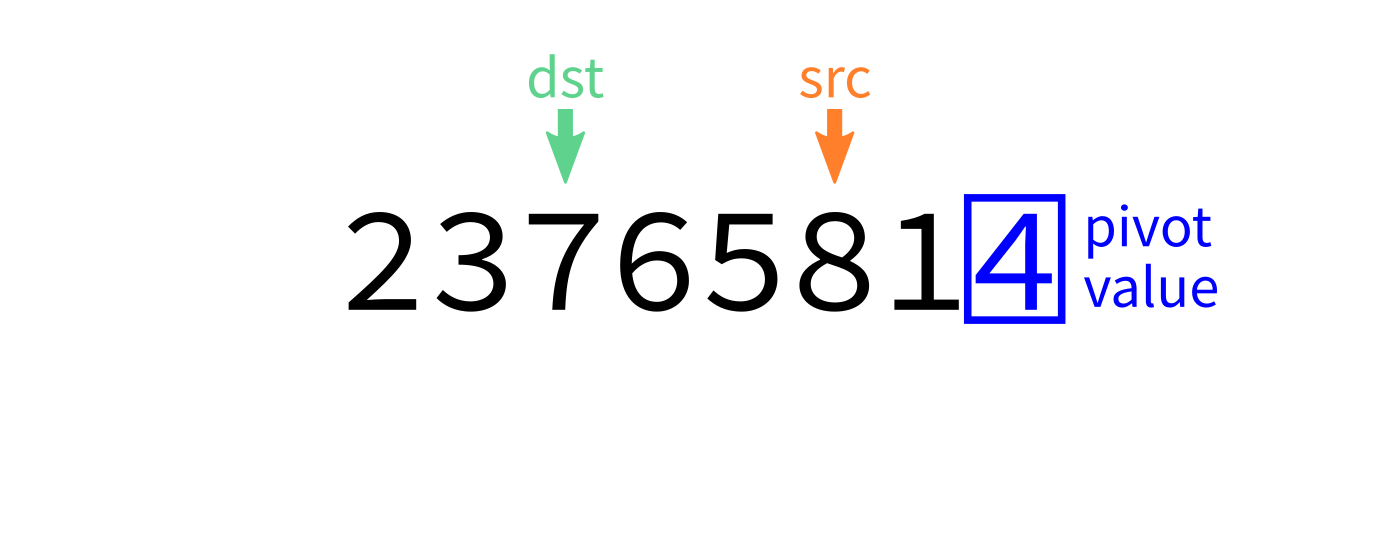
def partition(L,start,end):
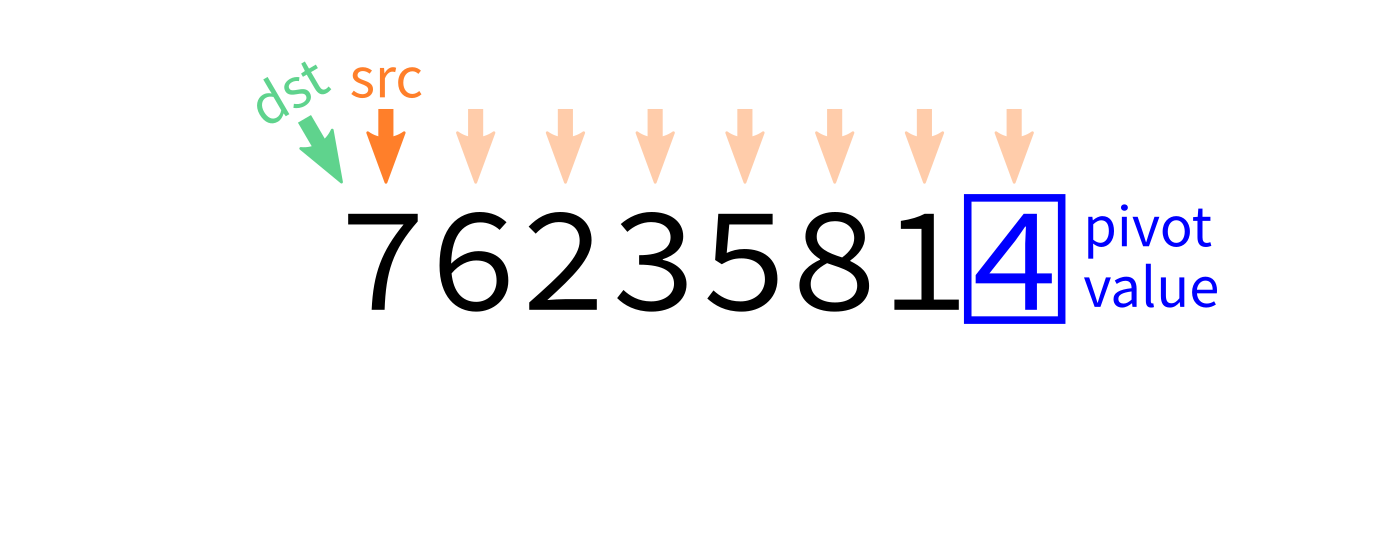
"""Look at L[start:end]. Take the last element as a pivot.
Move elements around so that any value less than the pivot
appears before it, and any element greater than or equal to
the pivot appears after it. L is modified in place. The
final location of the pivot is returned."""
# TODO: Add code hereNote this function uses the last element as a pivot. Later we'll discuss other options.
Coding time
Let's implement quicksort in Python.
quicksort:
Input: list L and indices start and end.
Goal: reorder elements of L so that L[start:end] is sorted.
- If
(end-start)is less than or equal to 1, return immediately. - Otherwise, call
partition(L)to partition the list, lettingmbe the final location of the pivot. - Call
quicksort(L,start,m)andquicksort(L,m+1,end)to sort the parts of the list on either side of the pivot.
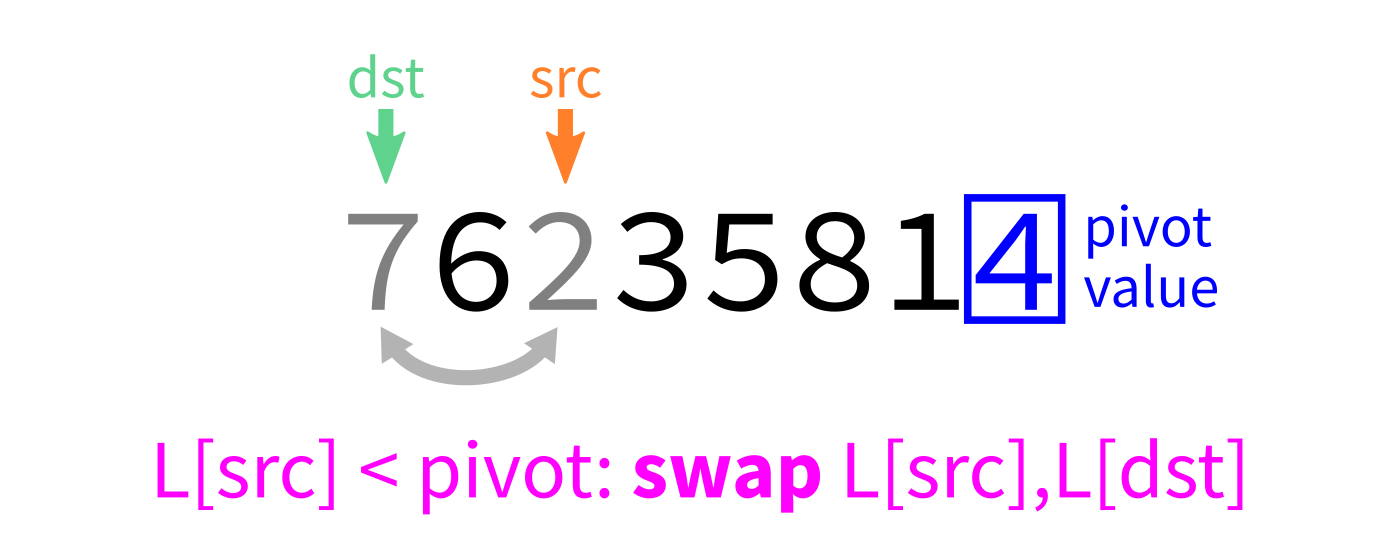
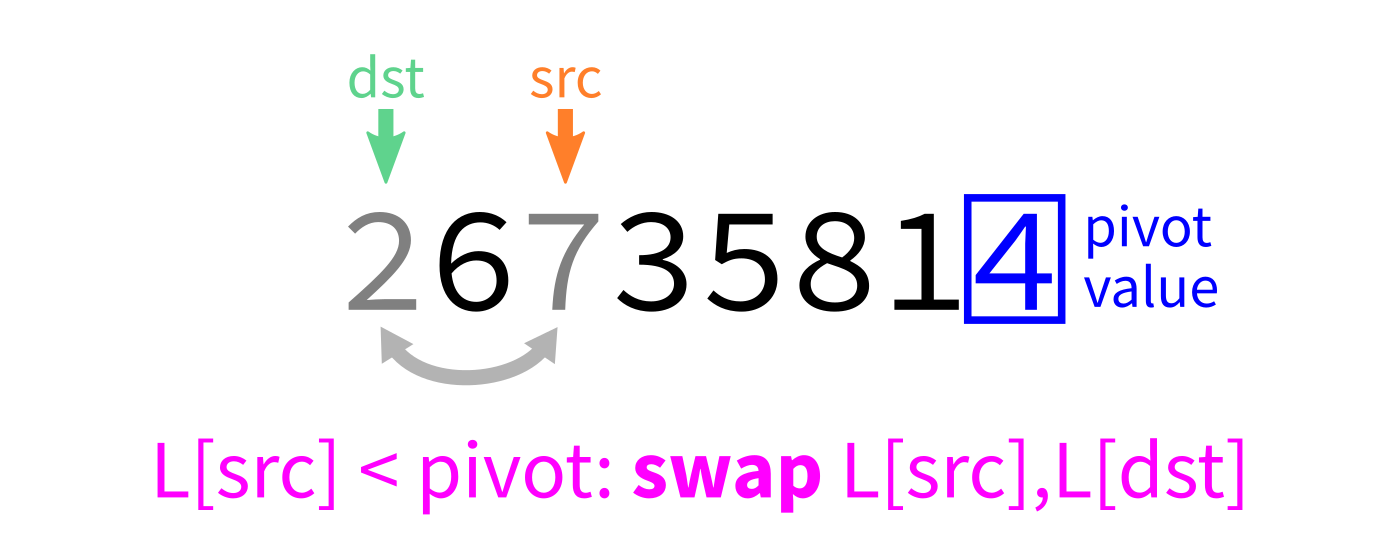
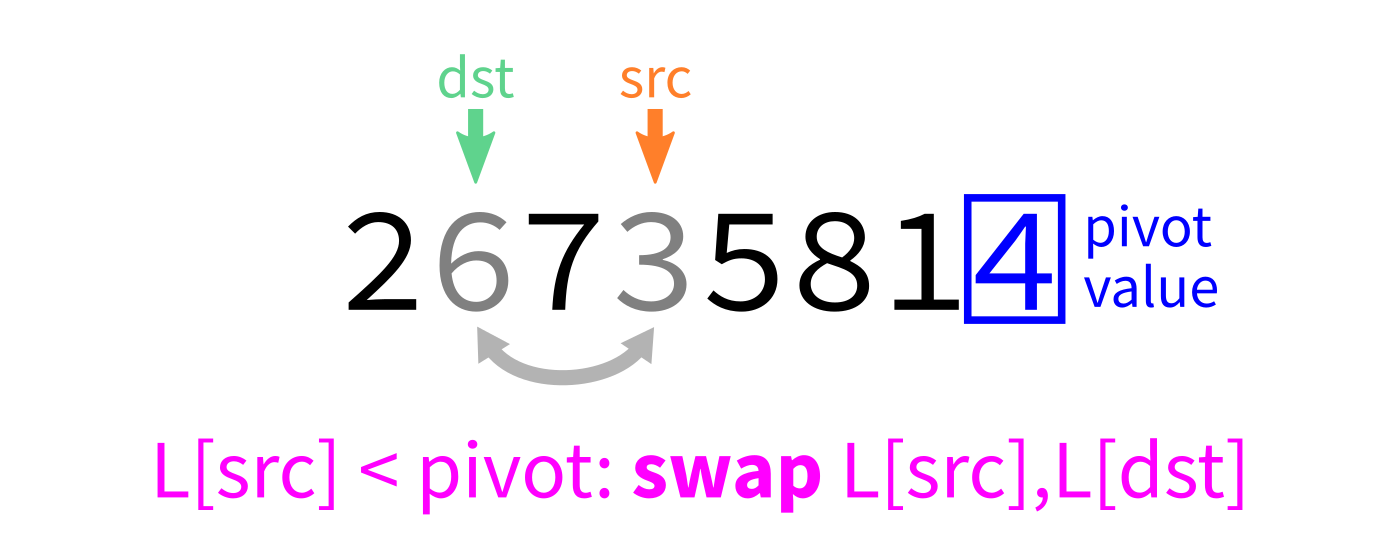
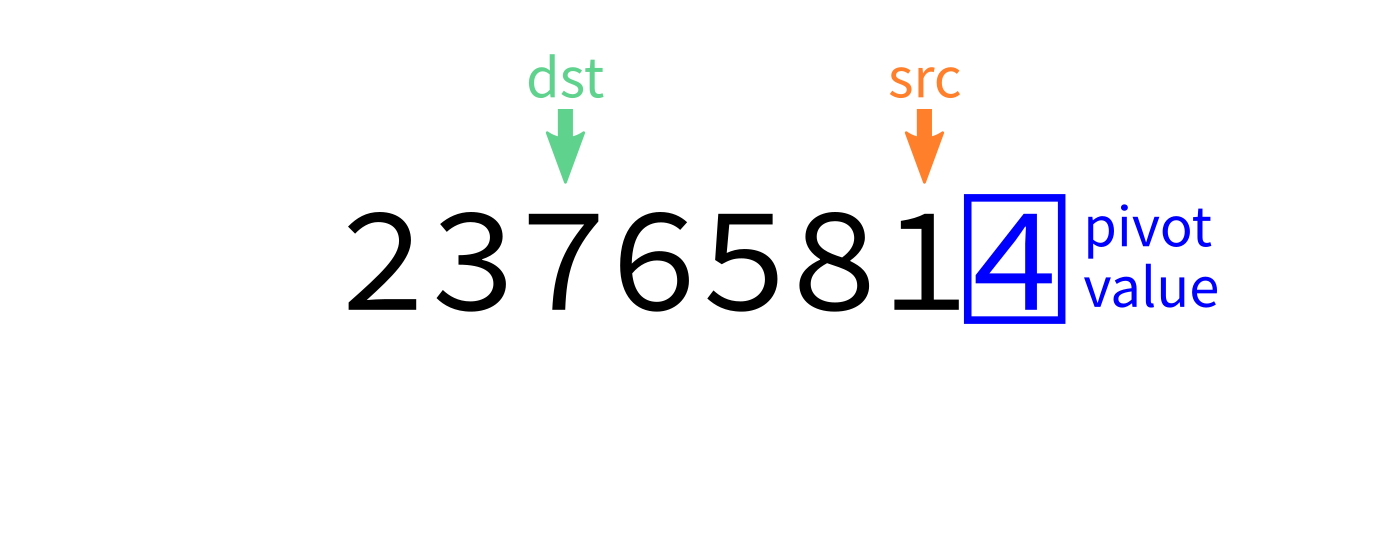
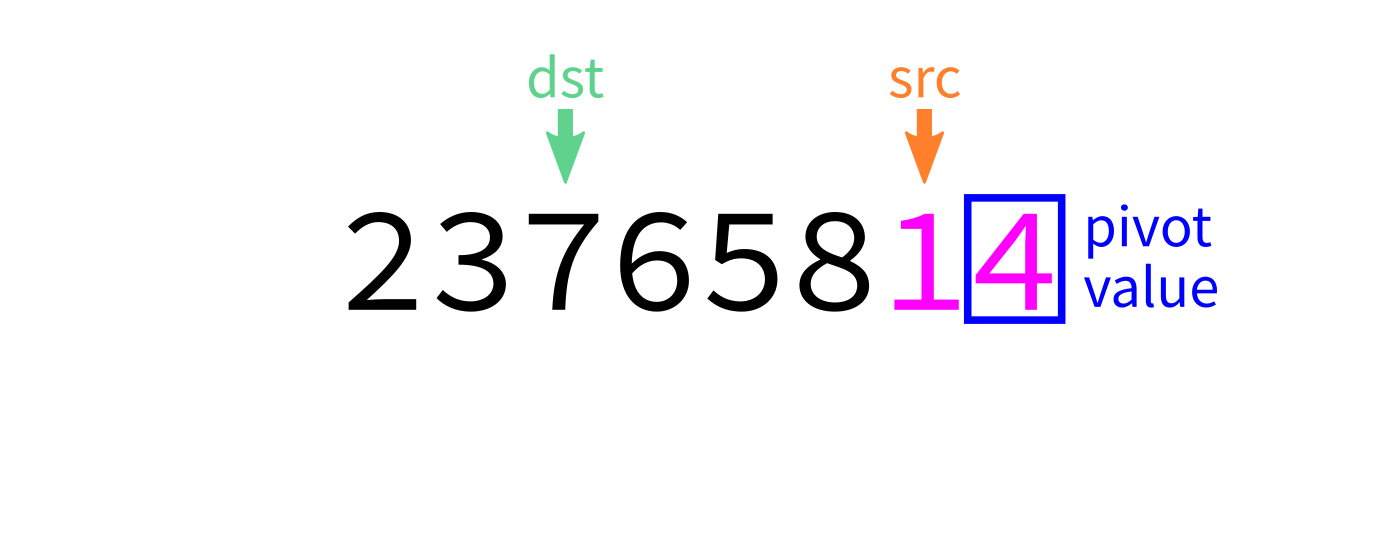
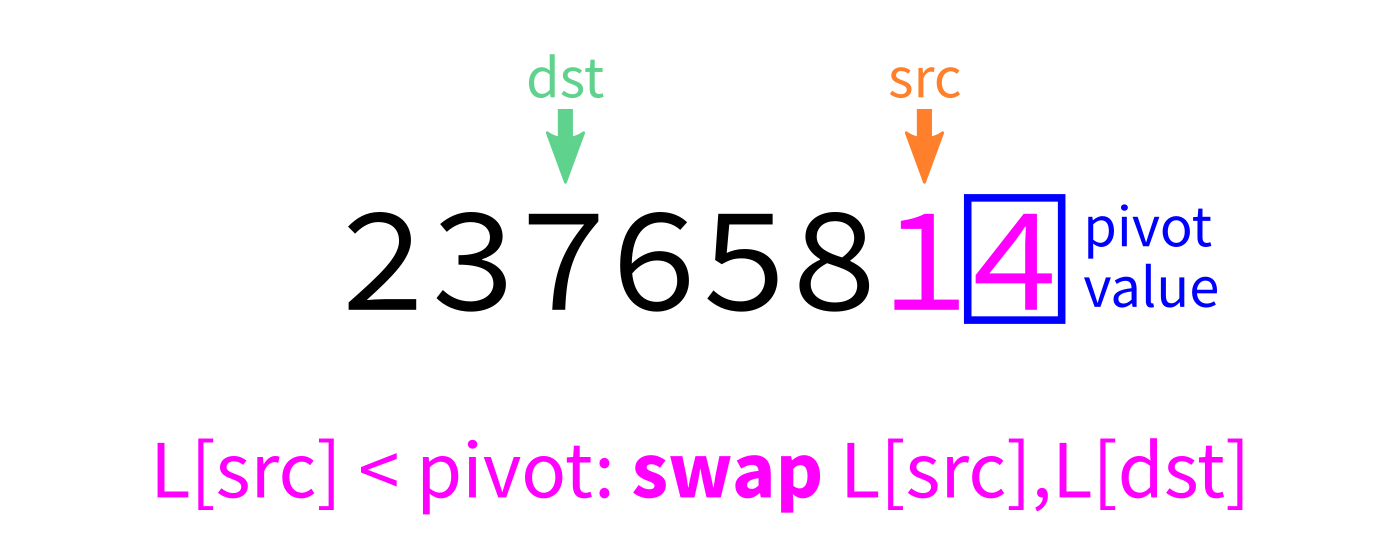
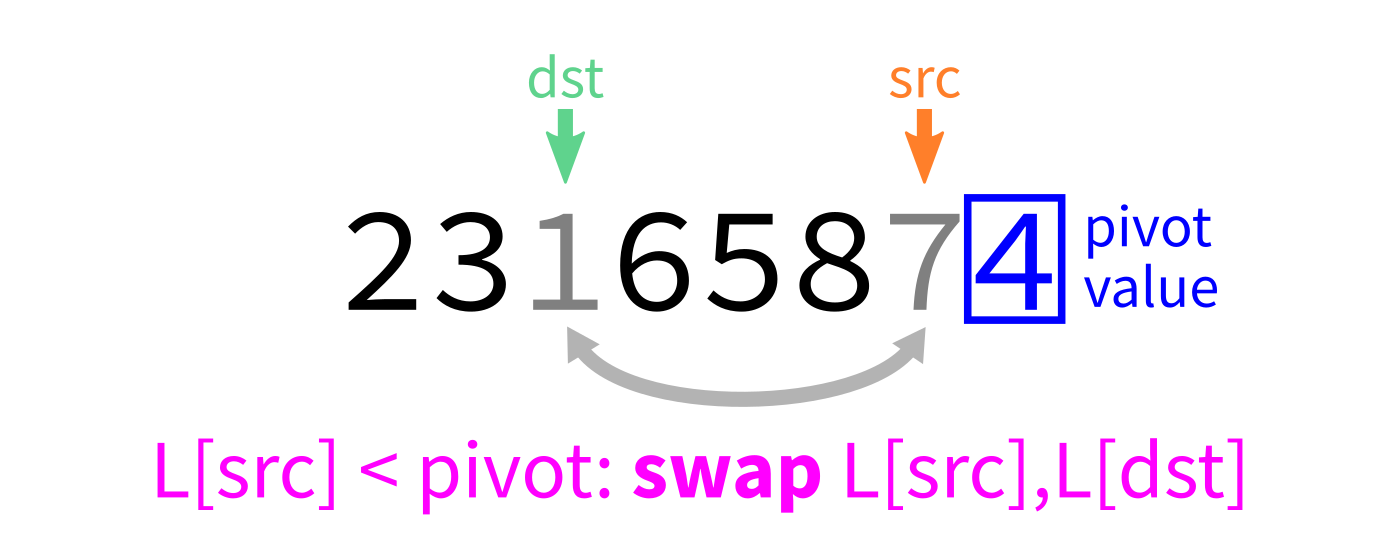
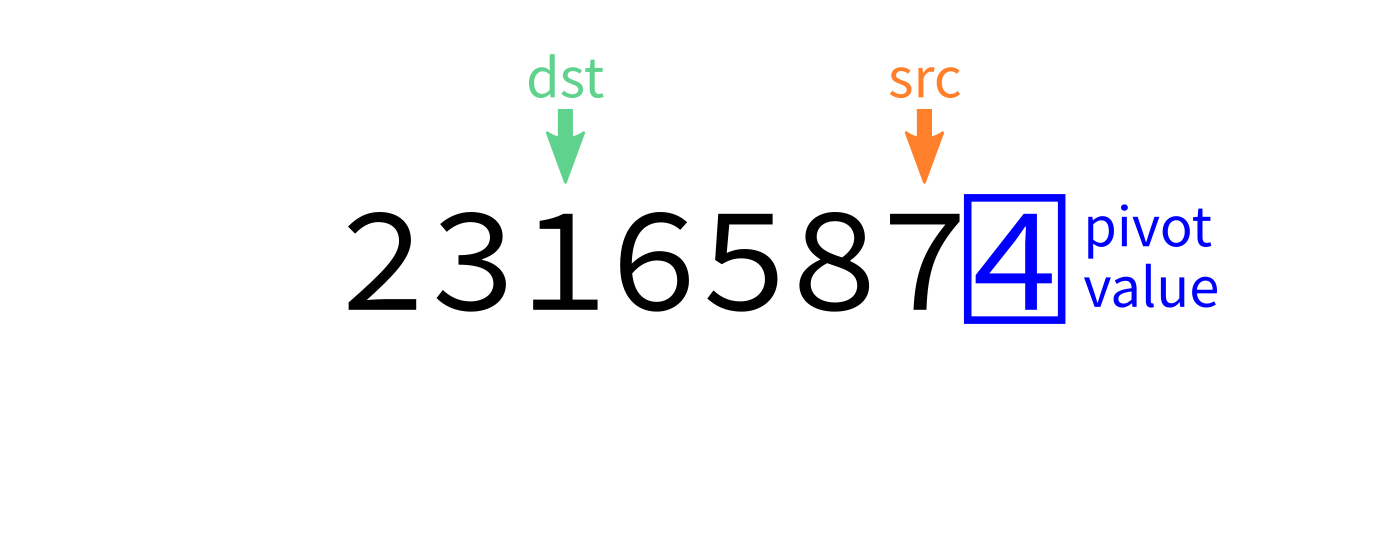
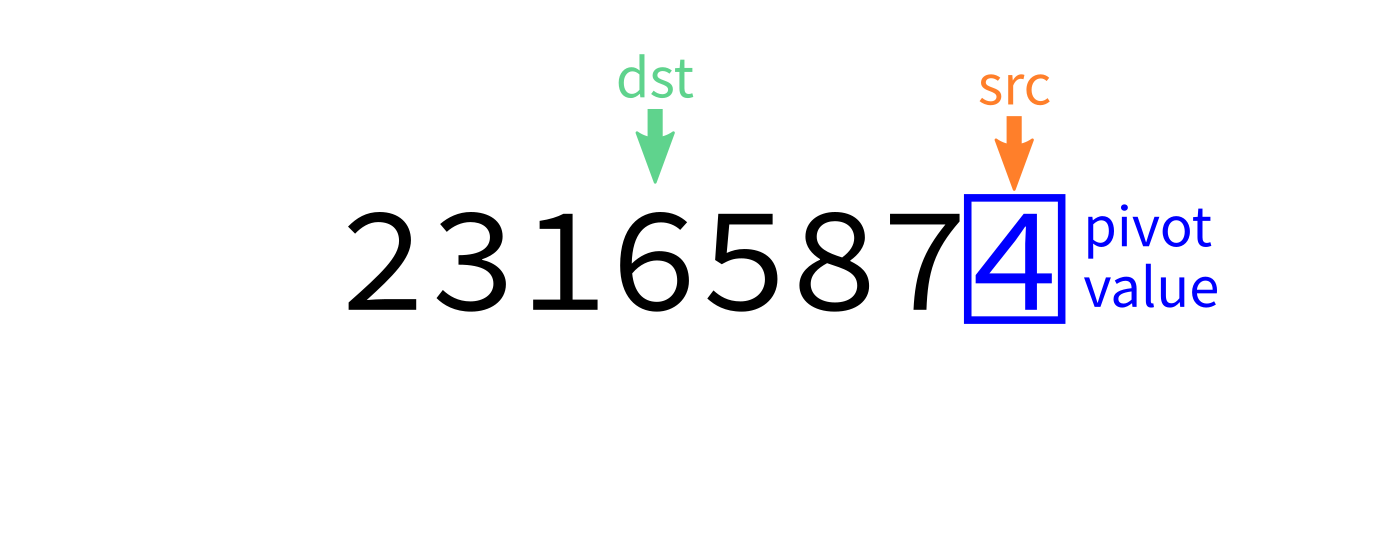
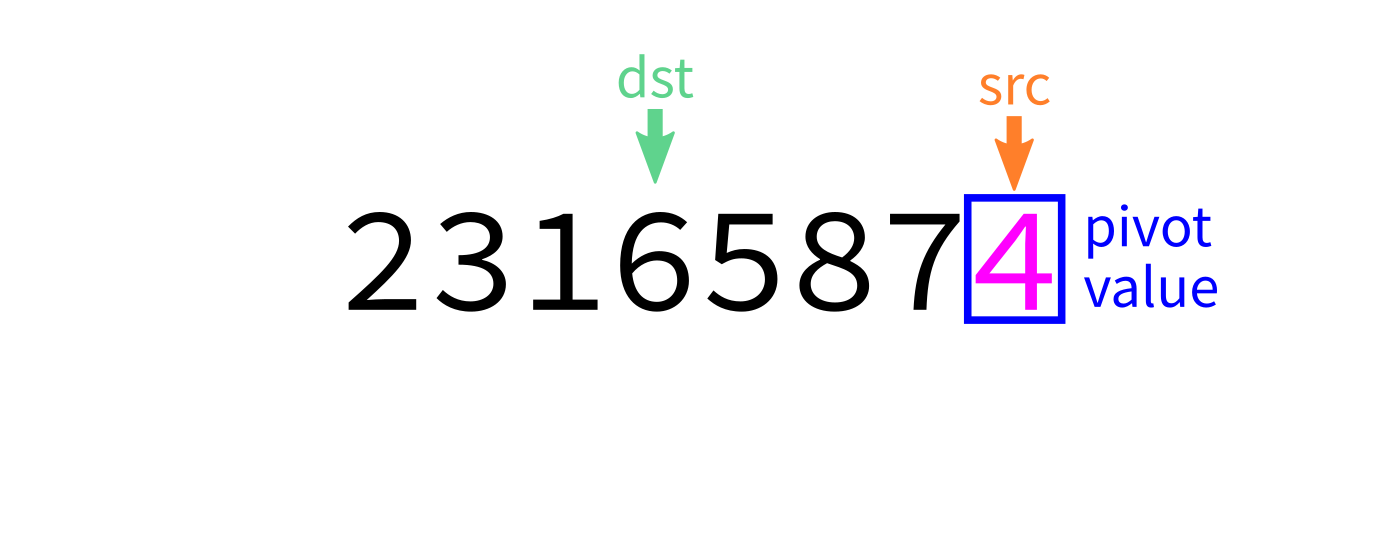
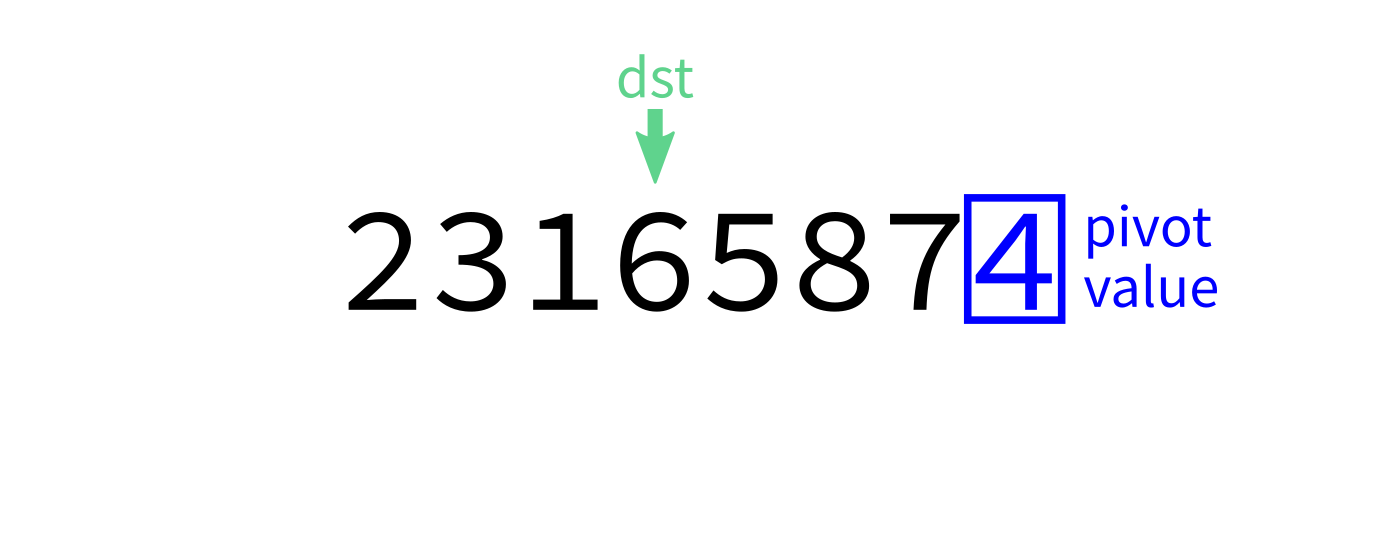
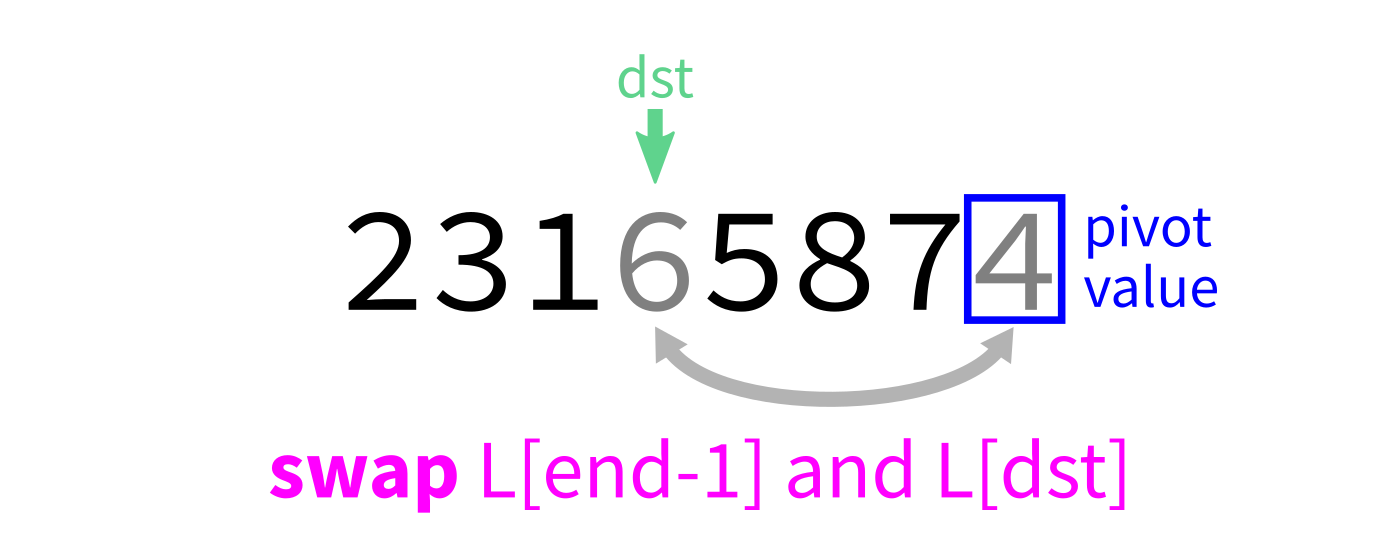
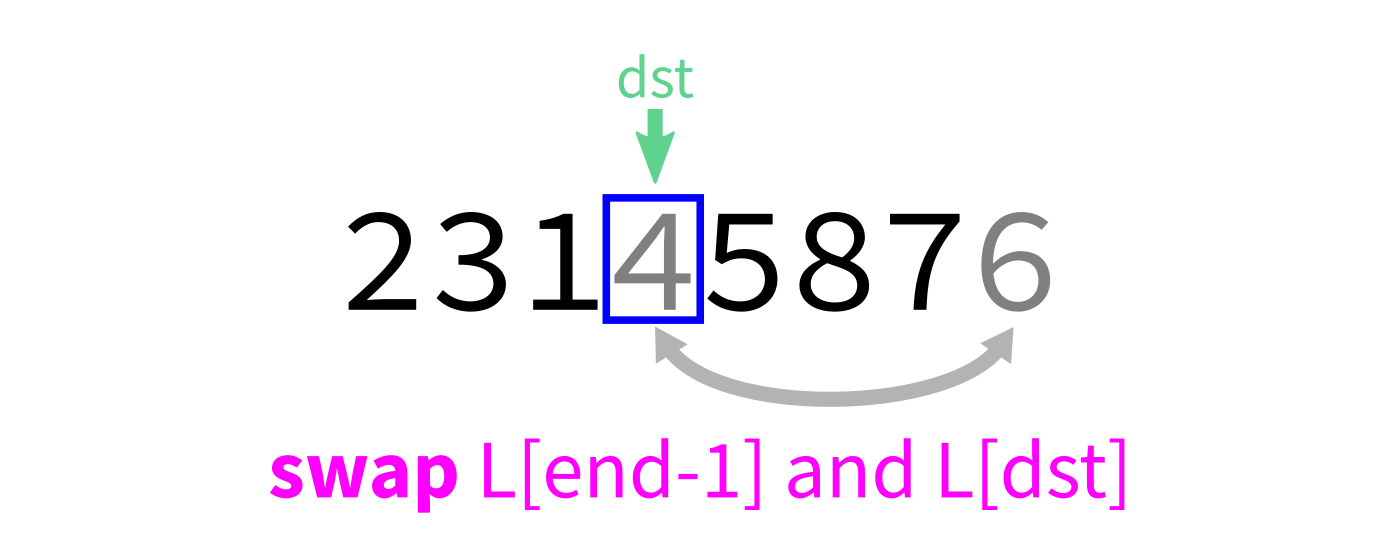
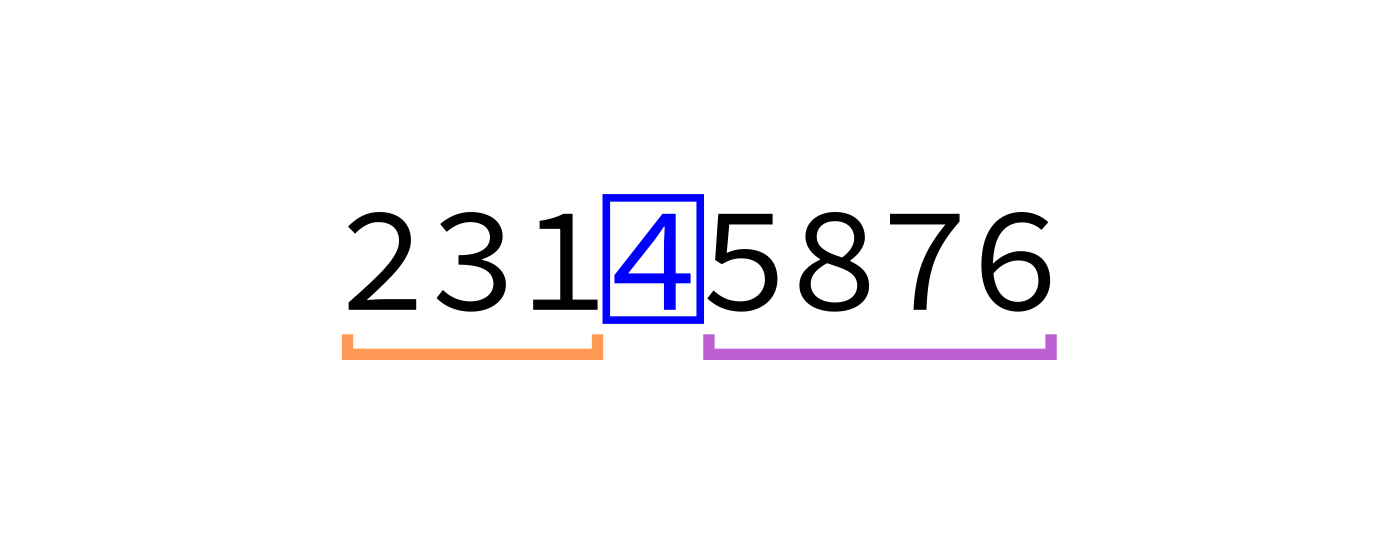
Partition
How to write partition(L,start,end)?
Recall we plan to make a version that uses the last element of L[start:end] as the pivot.
Partition visualization

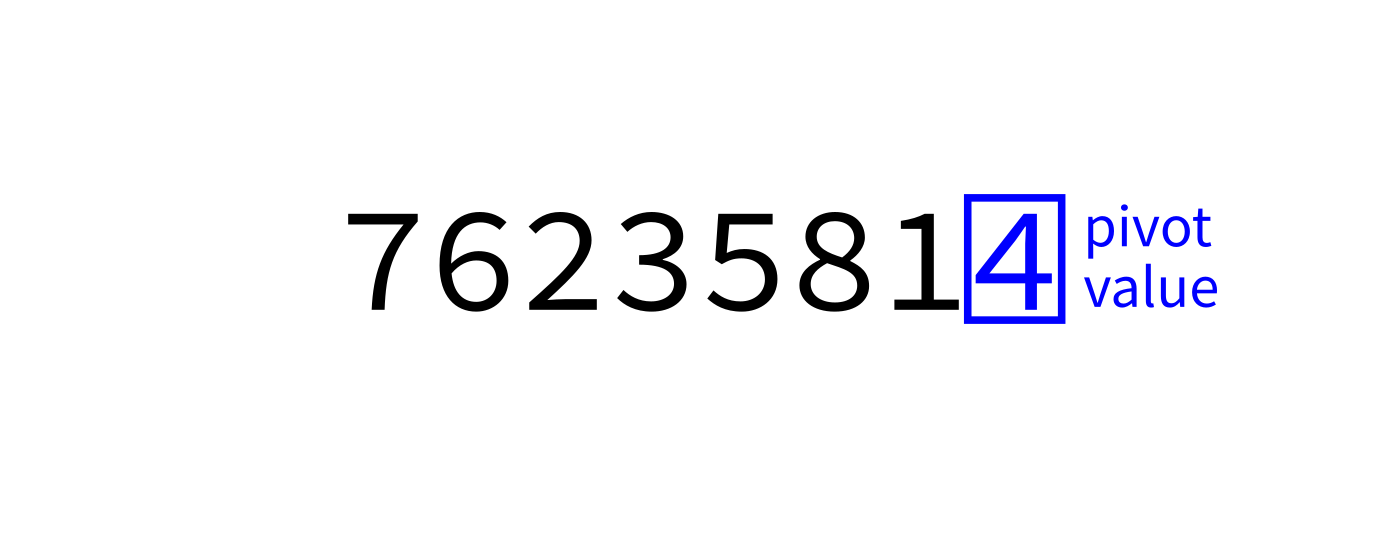

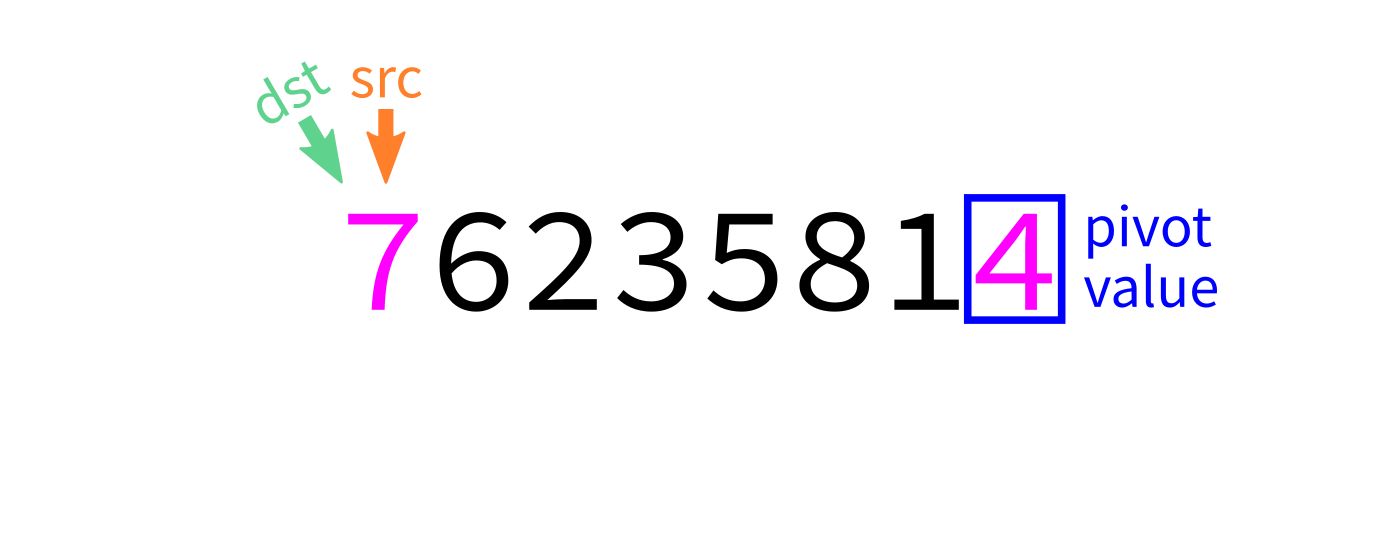
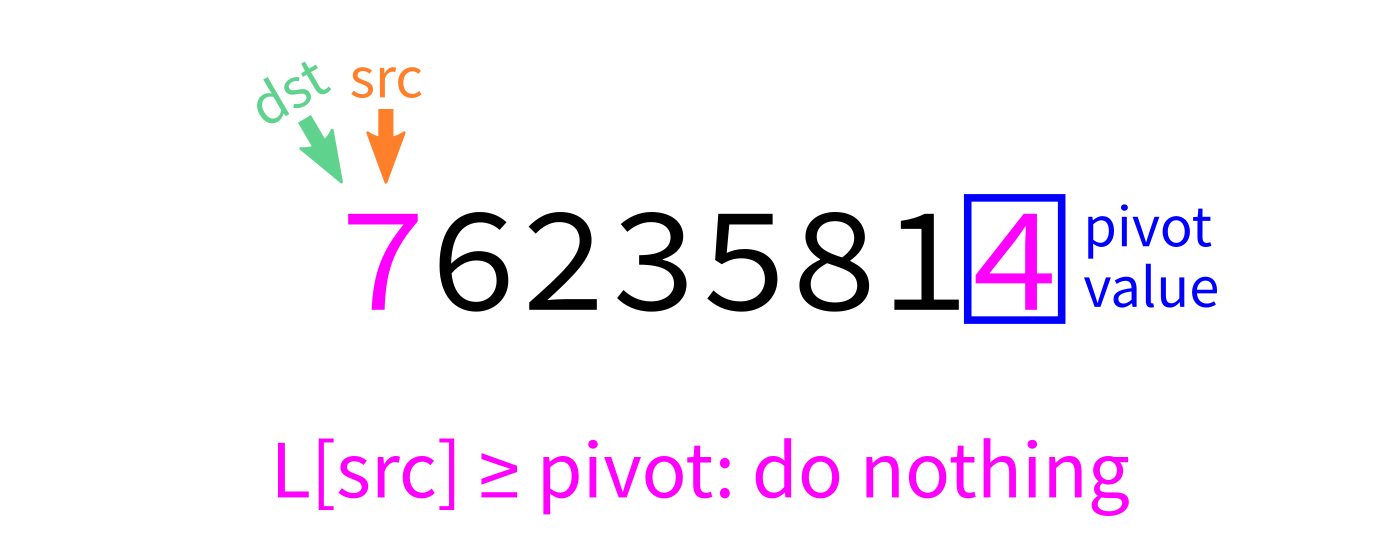
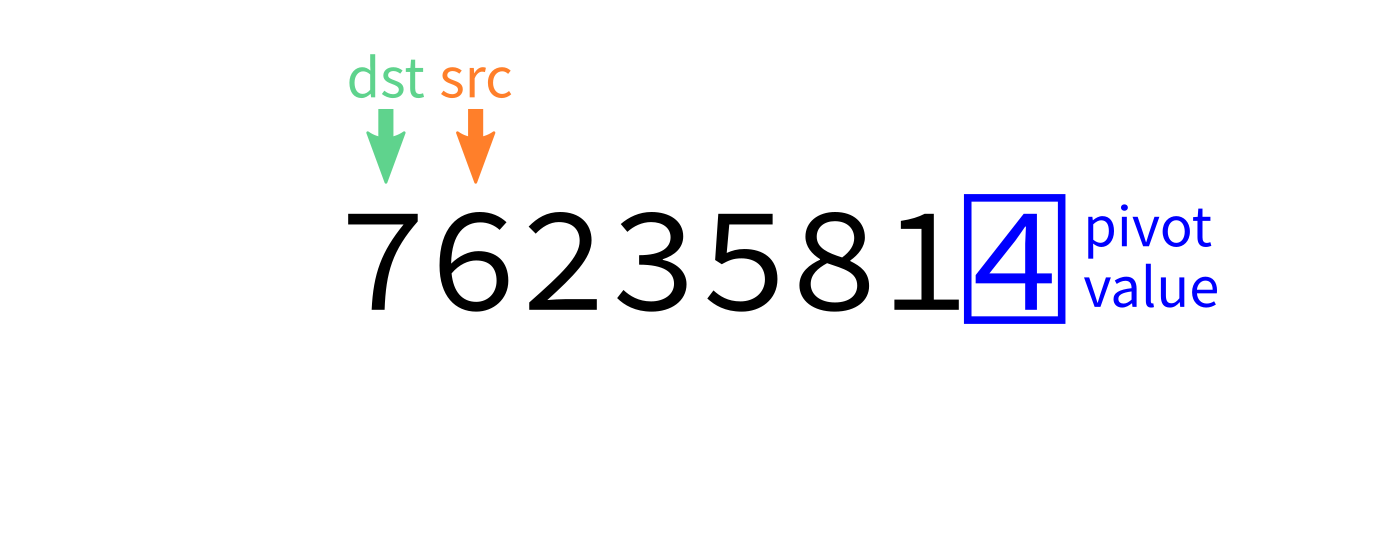
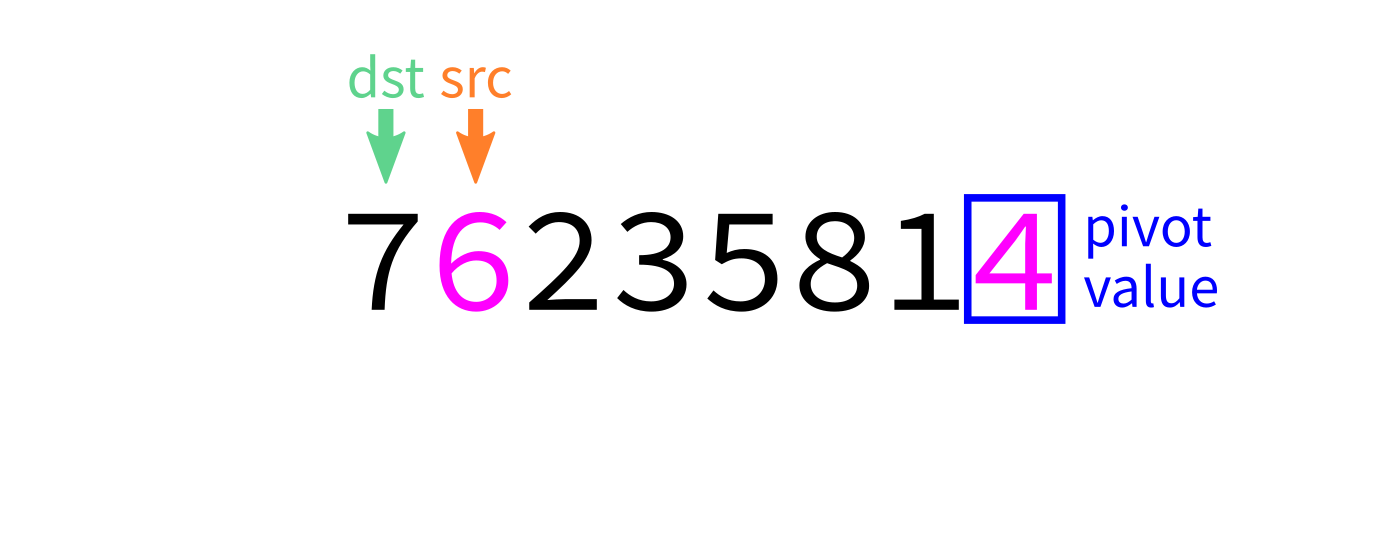
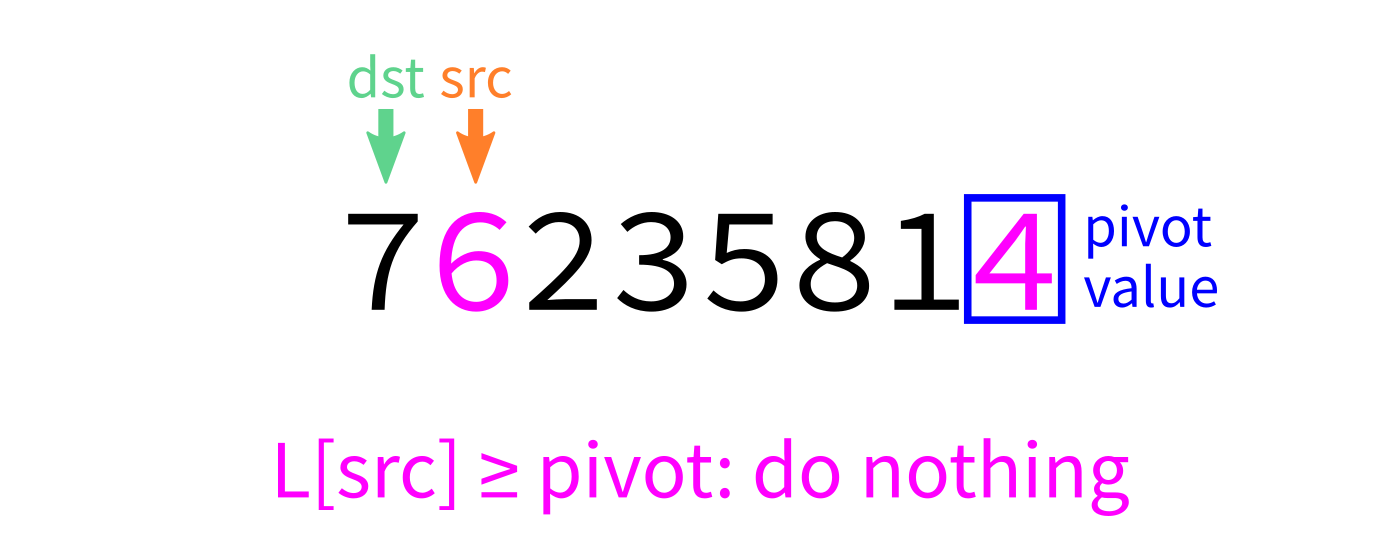

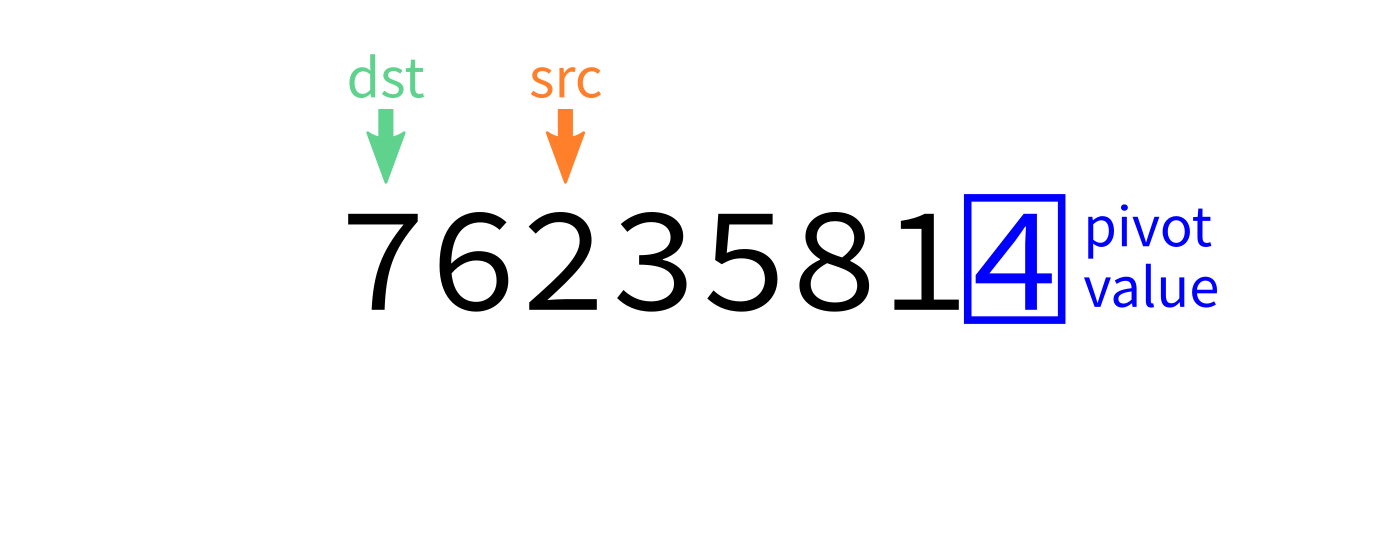
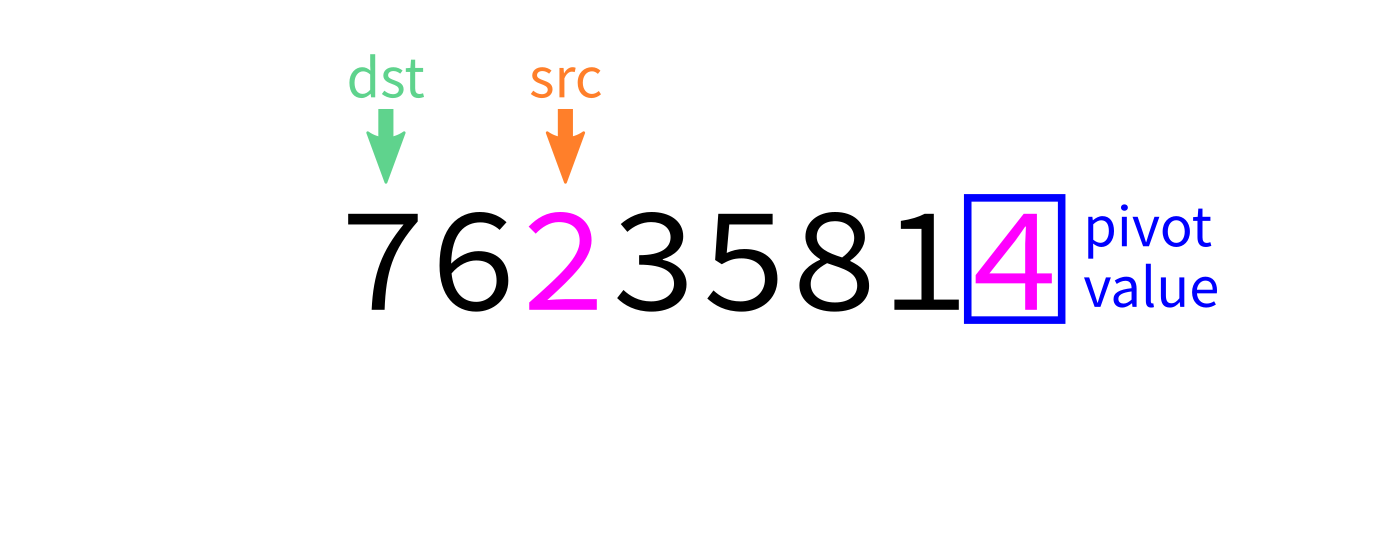










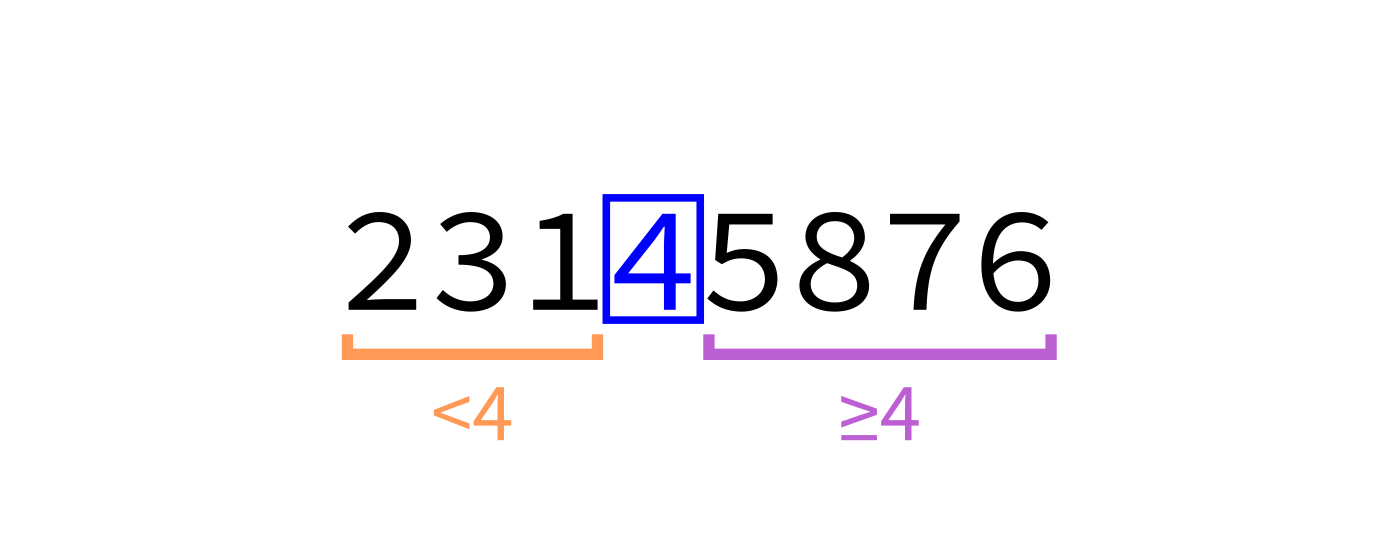
References
- You can refer to the general references about recursion that have appeared in several recent lectures. The rest of this list is specific to mergesort and quicksort.
- Making nice visualizations of sorting algorithms is a cottage industry in CS education. Some you might like to check out:
- 2D visualization through color sorting by Linus Lee
- Animated bar graph visualization of many sorting algorithms by Alex Macy
- Slanted line animated visualizations of mergesort and quicksort by Mike Bostock
Revision history
- 2021-02-22 Moved unused slides to Lecture 18 and fix partition visualization
- 2021-02-17 Fix description of partition step in quicksort preview
- 2021-02-17 Initial publication