MCS 275 Spring 2024 Homework 9¶
- Course Instructor: Emily Dumas
Deadline¶
This homework assignment must be submitted in Gradescope by Noon central time on Tuesday March 12, 2024.
Collaboration¶
Collaboration is prohibited, and while working on this you should only consult the resources (books, online, etc.) listed below.
Content¶
This assignment corresponds to Worksheet 9 and is about the basics of numpy and its use with pillow.
Resources you may consult¶
The materials you may refer to for this homework are:
Most likely useful
- Worksheet 9
- Worksheet 9 Solutions - This link will work once the solutions are posted
- Lecture 21 - numpy 1
- Lecture 22 - numpy 2
- Lecture 23 - Julia sets
- VanderPlas:
- Chapter 2 covers numpy
- Course sample code repo
- Especially /numpy_matplotlib/
- Allowed, but less likely to be useful:
- Any of the MCS 275 lecture materials, worksheets, previous homework assignments, or solutions to these, if posted on the course Blackboard site.
- Slides from any lecture of my MCS 260 course from Fall 2021.
- Any lecture video posted on the MCS 275 Blackboard site
- Any textbook listed on the course blackboard site under "Textbooks"
Point distribution¶
This homework assignment has two problems. The grading breakdown is:
| Points | Item |
|---|---|
| 4 | Autograder syntax checks (problem 1) |
| 5 | Problem 2 |
| 5 | Problem 3 |
| 14 | Total |
What to do if you're stuck¶
Ask your instructor or TA a question by email, in office hours, or on discord.
Problem 2: Matrix stippling¶
Work in hwk9prob2.py.
Suppose you have a matrix $M$, a positive integer $k$, and we choose one of the entries of $M$. From this information, we can make a new matrix as follows: We start at the chosen entry of $M$, and then find all the other entries we can get to by moving $k$ columns left or right, $k$ rows up or down, or any combination thereof. This gives a collection of entries of $M$ that we can group into their own, smaller matrix. We call the result a $k$-stipple of $M$.
For example, here is an example of a matrix $M$ and two different $3$-stipples of it. In the image below, the starting entry of $M$ is highlighted in blue, and all the other entries we get to by taking steps of size $k$ are highlighted in purple.
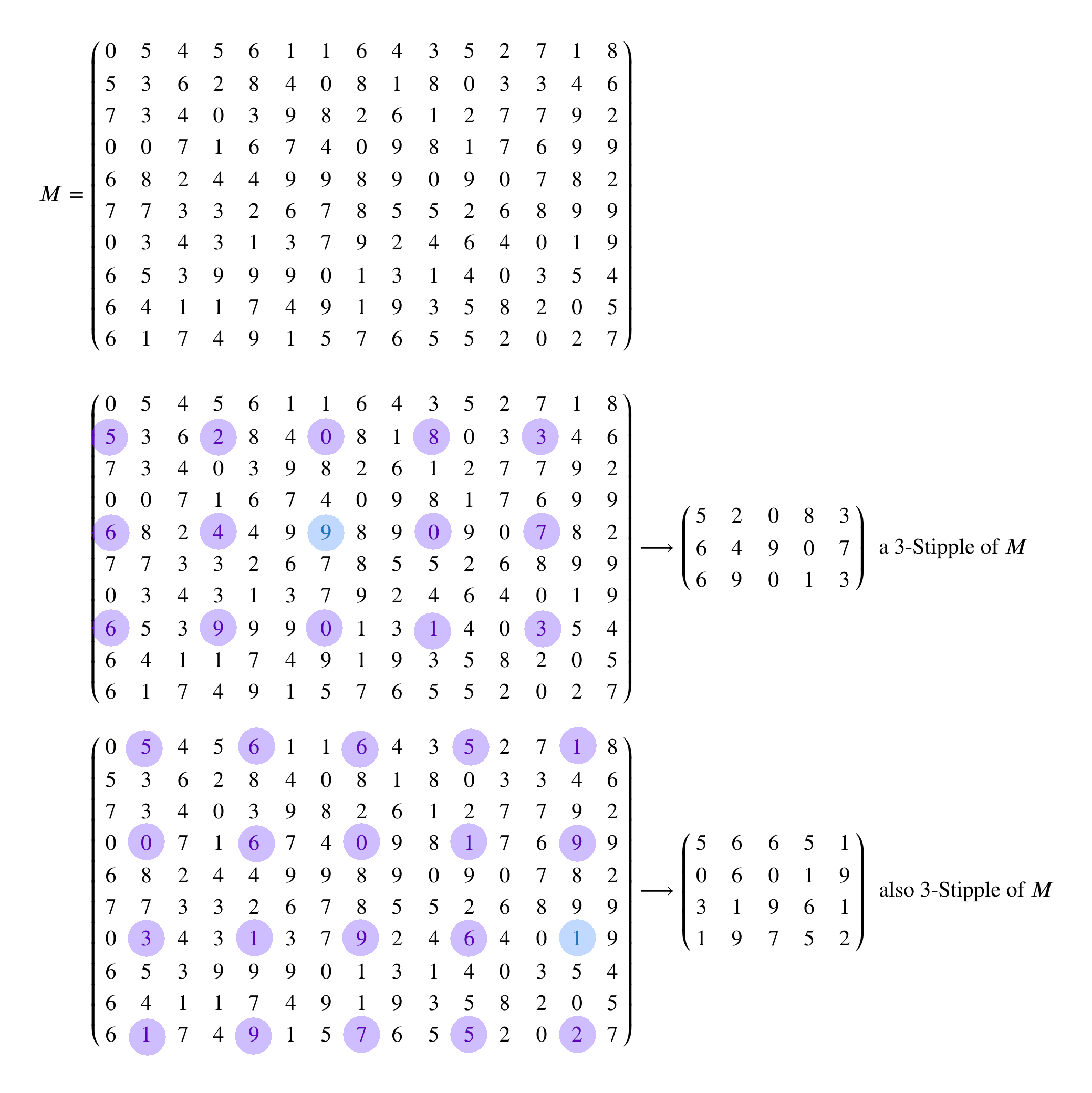
Note that sometimes two different starting entries in $M$ give the same $k$-stipple. This happens exactly when one of the entries is reachable from the other by steps of size $k$.
Also, if $k=1$ then the only $1$-stipple of $M$ is $M$ itself.
With this definition in mind, write a function matching the definition and description given in the docstring below.
def stipple_related(A,B,k):
"""
Given two numpy matrices `A` and `B` (that is, 2-dimensional
numpy arrays) and a positive integer `k`, returns a boolean
that indicates whether one of the matrices is a `k`-stipple
of the other. That is, returns:
True if A is a `k`-stipple of B,
True is B is a `k`-stipple of A,
False otherwise
"""
Important: For full credit your solution needs to make proper use of numpy to do its work. You can use Python loops, but the number of iterations they involve shouldn't depend on the sizes of A and B. Anything that requires iteration over something depending on matrix size should be handled by the proper numpy construct.
Problem 3: Gamma to match¶
Work in hwk9prob3.py.
Recall from Worksheet 9 that if $\gamma$ is a positive real number, then applying a $\gamma$-correction to a grayscale image means the following:
- Divide the image data matrix by 255 so it becomes an array of floats between 0 and 1
- Raise every entry in the matrix to the power $\gamma$
- Multiply by 255 again and convert to an array of
uint8objects (m.astype("uint8")does this for an arraym). - Use this as the new image data.
Write a function that takes two filenames, a reference image filename and a target image filename. It should load both image files into numpy arrays and compute the average brightness of pixels in the reference image (call this the reference brightness). Its goal is then to find and return a value of $\gamma$ (a positive real number) so that applying $\gamma$-correction to the target image results in it having the same average brightness as the reference brightness.
To do this without analyzing how the average brightness depends on $\gamma$, we'll assume that we just want to know which $\gamma$ that is a multiple of $0.1$ and which lies between $0.2$ and $20$ gives the closest match between average brightnesses. That means you need only test values $0.2, 0.3, 0.4, \ldots, 19.8, 19.9, 20$ and choose the one giving the best match. (In case of an exact tie, use the smaller $\gamma$.)
Here's a function definition and docstring to use.
def matching_gamma(reference_fn, target_fn):
"""
Loads the images in the files whose names are given by `reference_fn`
and `target_fn` (both strings).
Among real numbers `gamma` that are multiples of 0.1 and lie between
0.2 and 20, find the one which gives the best gamma-correction factor
to apply to the target image in order to make its average brightness
match the reference image.
"""
Revision history¶
- 2024-02-29 Initial publication