MCS 275 Spring 2024 Homework 9 Solutions¶

Course Instructor: Emily Dumas

Problem 2: Matrix stippling¶

Work in hwk9prob2.py.

Suppose you have a matrix $M$, a positive integer $k$, and we choose one of the entries of $M$. From this information, we can make a new matrix as follows: We start at the chosen entry of $M$, and then find all the other entries we can get to by moving $k$ columns left or right, $k$ rows up or down, or any combination thereof. This gives a collection of entries of $M$ that we can group into their own, smaller matrix. We call the result a $k$-stipple of $M$.

For example, here is an example of a matrix $M$ and two different $3$-stipples of it. In the image below, the starting entry of $M$ is highlighted in blue, and all the other entries we get to by taking steps of size $k$ are highlighted in purple.

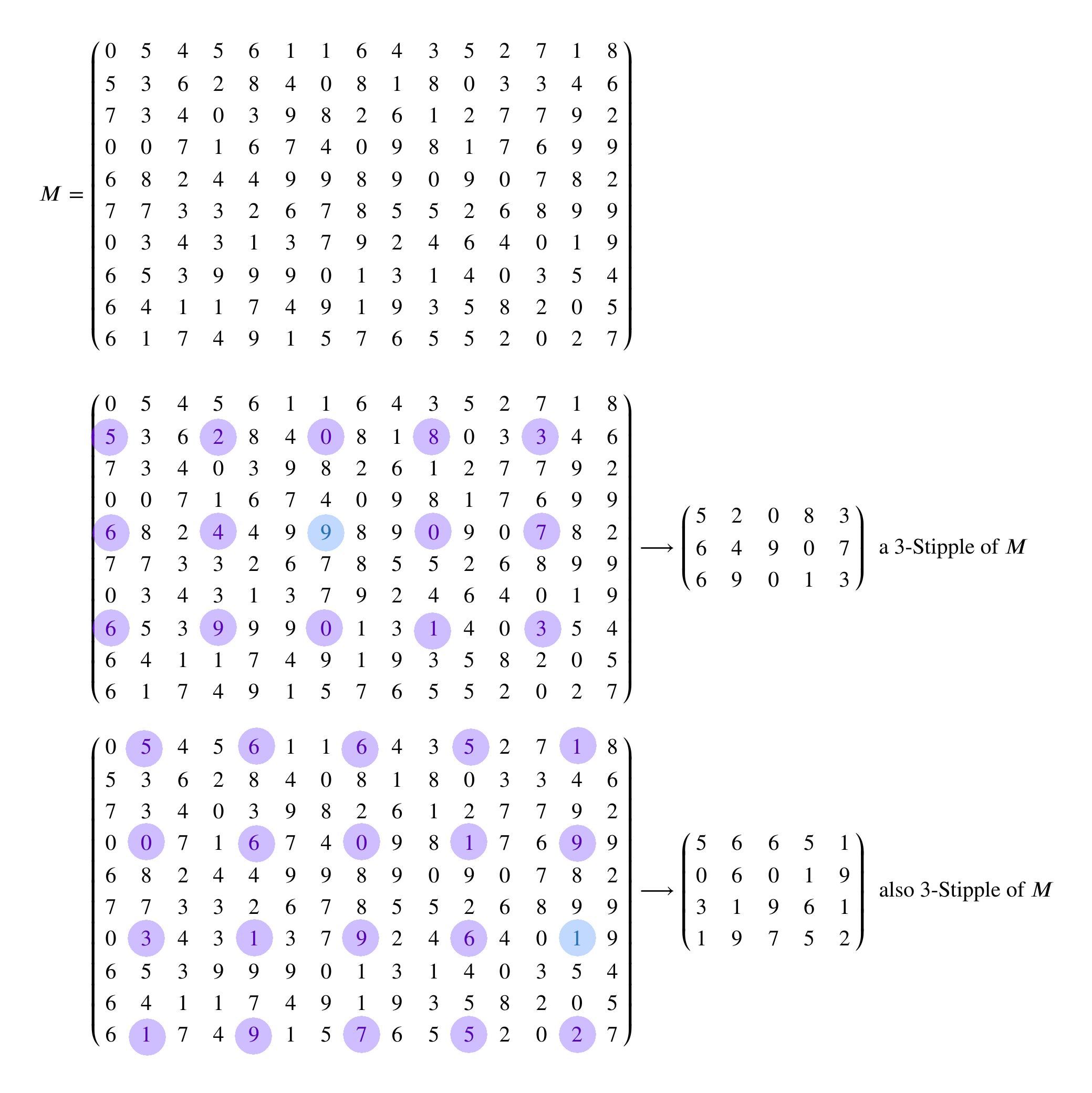
stippling a matrix, two examples

Note that sometimes two different starting entries in $M$ give the same $k$-stipple. This happens exactly when one of the entries is reachable from the other by steps of size $k$.

Also, if $k=1$ then the only $1$-stipple of $M$ is $M$ itself.

With this definition in mind, write a function matching the definition and description given in the docstring below.

def stipple_related(A,B,k):
    """
    Given two numpy matrices `A` and `B` (that is, 2-dimensional
    numpy arrays) and a positive integer `k`, returns a boolean
    that indicates whether one of the matrices is a `k`-stipple
    of the other.  That is, returns:
        True if A is a `k`-stipple of B,
        True is B is a `k`-stipple of A,
        False otherwise
    """

Important: For full credit your solution needs to make proper use of numpy to do its work. You can use Python loops, but the number of iterations they involve shouldn't depend on the sizes of A and B. Anything that requires iteration over something depending on matrix size should be handled by the proper numpy construct.

import numpy as np

def stipple_related(A,B,k):
    """
    Given two numpy matrices `A` and `B` (that is, 2-dimensional
    numpy arrays) and a positive integer `k`, returns a boolean
    that indicates whether one of the matrices is a `k`-stipple
    of the other.  That is, returns:
        True if A is a `k`-stipple of B,
        True is B is a `k`-stipple of A,
        False otherwise
    """
    # Make A the bigger one by switching if A has fewer rows
    if A.shape[0] < B.shape[0]:
        A,B = B,A
    # If A now has more columns, then neither is bigger
    # than the other, so is not a k-stipple.
    if A.shape[1] < B.shape[1]:
        return False
    # Now check every possible k-stipple of A and see if
    # it is equal to B
    for i in range(k):
        for j in range(k):
            if np.array_equal(A[i::k,j::k],B):
                return True
    return False

Problem 3: Gamma to match¶

Work in hwk9prob3.py.

Recall from Worksheet 9 that if $\gamma$ is a positive real number, then applying a $\gamma$-correction to a grayscale image means the following:

Divide the image data matrix by 255 so it becomes an array of floats between 0 and 1
Raise every entry in the matrix to the power $\gamma$
Multiply by 255 again and convert to an array of uint8 objects (m.astype("uint8") does this for an array m).
Use this as the new image data.

Write a function that takes two filenames, a reference image filename and a target image filename. It should load both image files into numpy arrays and compute the average brightness of pixels in the reference image (call this the reference brightness). Its goal is then to find and return a value of $\gamma$ (a positive real number) so that applying $\gamma$-correction to the target image results in it having the same average brightness as the reference brightness.

To do this without analyzing how the average brightness depends on $\gamma$, we'll assume that we just want to know which $\gamma$ that is a multiple of $0.1$ and which lies between $0.2$ and $20$ gives the closest match between average brightnesses. That means you need only test values $0.2, 0.3, 0.4, \ldots, 19.8, 19.9, 20$ and choose the one giving the best match. (In case of an exact tie, use the smaller $\gamma$.)

Here's a function definition and docstring to use.

def matching_gamma(reference_fn, target_fn):
    """
    Loads the images in the files whose names are given by `reference_fn`
    and `target_fn` (both strings).
    Among real numbers `gamma` that are multiples of 0.1 and lie between
    0.2 and 20, find the one which gives the best gamma-correction factor
    to apply to the target image in order to make its average brightness
    match the reference image.
    """

Solution¶

from PIL import Image

def matching_gamma(reference_fn, target_fn):
    """
    Loads the images in the files whose names are given by `reference_fn`
    and `target_fn` (both strings).
    Among real numbers `gamma` that are multiples of 0.1 and lie between
    0.2 and 20, find the one which gives the best gamma-correction factor
    to apply to the target image in order to make its average brightness
    match the reference image.
    """
    ref_img = Image.open(reference_fn)
    target_img = Image.open(target_fn)
    # Make grayscale if needed
    if ref_img.mode != "L":
        ref_img = ref_img.convert("L")
    if target_img.mode != "L":
        target_img = target_img.convert("L")
    # Make into float arrays
    refA = np.array(ref_img) / 255.0
    targetA = np.array(target_img) / 255.0
    # Average brightness
    ref_brightness = np.mean(refA)
    # Gammas under consideration
    # (We store as integers and later divide by 10 to get
    # exact steps of 0.1 instead of accumulating float error)
    ten_gammas = range(2,201)
    # Brightness of gamma-corrected target images
    results = np.array([ np.mean(targetA**(c/10.0)) for c in ten_gammas ])
    # Where is this closest to ref_brightness?
    i = np.argmin( np.abs(results - ref_brightness) )
    return ten_gammas[i]/10.0

Revision history¶

2024-04-02 Initial publication