MCS 275 Spring 2024 Project 3 - Tree of data blocks¶

• Course Instructor: Emily Dumas

Instructions:¶

Deadline is 11:59pm central time on Friday March 15, 2024¶

Note that the hour of the deadline is not the same as for homework assignments.

On the day of the deadline, the instructor may not be able to answer questions received after 3pm.

Collaboration¶

Collaboration is prohibited. We want to evaluate you on the basis of what you can do by consulting the resources listed below, and without help from anyone other than course staff. Seeking or giving aid on this assignment is prohibited (except for asking course staff); doing so constitutes academic misconduct which can have serious consequences. If you are unsure about whether something is allowed, ask. The course syllabus contains more information about the course and university policies regarding academic honesty.

Topic¶

You'll build a data structure that stores a mutable sequence (supporting insert but not changes to existing items) as a binary tree of blocks. You will also write a program that performs some timing tests on this data structure.

Resources you are allowed to consult¶

• Documents and videos posted to the course web page
• Any textbook listed on the course blackboard site under "Textbooks"

Ask if you're not sure whether a resource falls into one of these categories, or if you think I missed a resource that seems necessary to complete the assignment.

What to do if you're stuck¶

Ask your instructor or TA a question by email, in office hours, or on discord.

The idea: Different ways to store a sequence¶

This section will put the project in context and describe the general idea. It doesn't contain any information that is strictly required to produce a correct solution.

List - contiguous, occasional resizing¶

Python's list object lets you add and remove items at any time---though as we've discussed, inserting items near the beginning of the list can be slow.

What actually happens behind the scenes is that when you create a new empty list, Python reserves an area of memory that can store a certain number of items. As you add things to the list, they go into this reserved area of memory. At some point the reserved area may become full. If it does, the next time you add something to the list Python will reserve an entirely new, larger region of memory, copy everything in the list over to that larger area, add the new item in, and then release the smaller reserved memory area that is no longer needed.

Binary tree - a new node with every insert¶

While list is great for an ordered sequence of values accessed by index, you could also store that kind of data in a binary search tree. You could make the indices the keys of the nodes, and have each node also contain a value attribute that contains the item at that position in the list. This would have some nice features, such as allowing a list where some indices exist and others do not, and making insertion at any position possible without a lot of copying of other elements to later positions. However, a new node would be created as part of each insert operation, which might be a slow operation.

Hybrid - a tree of fixed-size blocks¶

The focus of this project is making a class BlockNode that behaves a bit like list (storing an ordered sequence of values accessible by zero-based index, and supporting insertion of new items at any position) but which uses a hybrid of the two approaches discussed above. It will start with a list of a fixed length (6 in this assignment, but it could be any chosen constant) and store values there until it is full. Then it will make another BlockNode object, also having its own list of the chosen fixed length, to provide additional storage. This continues with all the BlockNodes made so far being arranged in a binary tree that keeps track of the order in which their small lists need to be joined together to get the entire sequence that is being stored. In theory, this should provide a list-like structure where insert at any position is pretty fast, but where the creation of new objects happens less frequently than in a binary search tree with only one item in each node.

Motivation: Block-based storage is common¶

There's another reason we might consider using a collection of lists of a fixed size to store a larger sequence: It could help make saving the sequence to disk or another storage medium more efficient.

In most cases, when a computer program writes data to a file, it ends up in a persistent storage medium---a device that can continue to store data even when the computer it is part of is powered off or restarted. Depending on the situation, that storage medium might be inside the computer you're using (e.g. an internal hard disk or SSD, or built-in flash memory of a smartphone), might be a separated device attached to it (a USB drive, an SD card in a professional camera, etc.), or it might be located inside a server housed in a distant datacenter (storage "in the cloud").

Persistent storage is different from memory, the temporary storage used for things like programs that are currently running and the variables and data structures those programs are using. Memory is cleared every time a device restarts or powers off.

Persistent storage devices typically don't work with individual bytes, characters, integers, or other units of data familiar from the work we've been doing in MCS 275. For example, you can't directly ask a USB flash drive to read one byte or one integer from a certain location. Instead, there's a fixed block size that the device works with, and every request to read or write something must involve a whole number of those blocks. Most USB flash drives use a block size of 4096 bytes, while the built-in flash memory of many smartphones uses a block size of 2112 bytes. Other block sizes are in use as well.

If you wanted to make an implementation of a list-like ordered sequence that was optimized for frequently saving it to a persistent storage medium, then it would be a good idea to organize it so that the structure was divided into pieces that each fit inside one of the blocks that the storage device uses. Further, you'd want to make it so that a small change to the sequence (like adding one item) changes only a few of the blocks, making it fast to save those changes to persistent storage. The BlockNode object you'll create here illustrates some of the ideas you might use to solve that kind of problem.

The programming details¶

This section contains the requirements for the Python module and program you need to write and submit.

No starter pack¶

There's nothing to download this time. You'll start from scratch and build the things requested below.

The two tasks¶

You must

1. Write a python module bstore.py that contains the things listed in the section below titled The Module.
2. Write a python program bstoredemo.py that does the things described in the section below titled The Program.

Both bstore.py and bstoredemo.py need to be uploaded to Gradescope for Project 3.

The Module¶

🛈 The autograder will test this module in detail 🛈

Create a file called bstore.py. It should define a single class called BlockNode that represents a node in a binary tree that will be used to store a list of integers (the data) that can have any length, and which supports insertion and retrieval by zero-based index.

When imported as a module, bstore.py must not do anything other than define a class. (If you like you can put test code in it that runs when bstore.py is executed as a script. Any such code will be ignored when grading.)

Attributes¶

In addition to the usual left, right, and parent attributes, each instance of the class has three other instance attributes:

• content, a list of 6 integers (initially [0,0,0,0,0,0]), some of which may be part of the data, and some of which may be unused at present (whatever value is will not matter, and they may be filled in later when more data is added)
• size, the number of elements from the beginning of the list content that contain actual data (initially 0)
• left_size, which contains the sum of all size attributes of nodes in the left subtree of this one. (The class must make sure this property is maintained whenever changes are made to the tree!)

The BlockNode class is not allowed to have any other instance attributes.

Meaning¶

The idea is that BlockNode simulates a fixed-size storage block that has enough room for 8 integers (6 for content, 1 for size, 1 for left_size) and two references to other BlockNodes (1 for left, 1 for right). If working with a storage system that only allowed blocks of that size, this would be one way to organize the storage of an arbitary-length list that allows efficient insertion of new elements at any position.

Diagrams will be helpful in explaining the behavior BlockNode must provide. Here's a picture of a BlockNode. Instead of indicating the size explicitly, we highlight the first size entries in the list content to indicate they contain data as opposed to unused space.

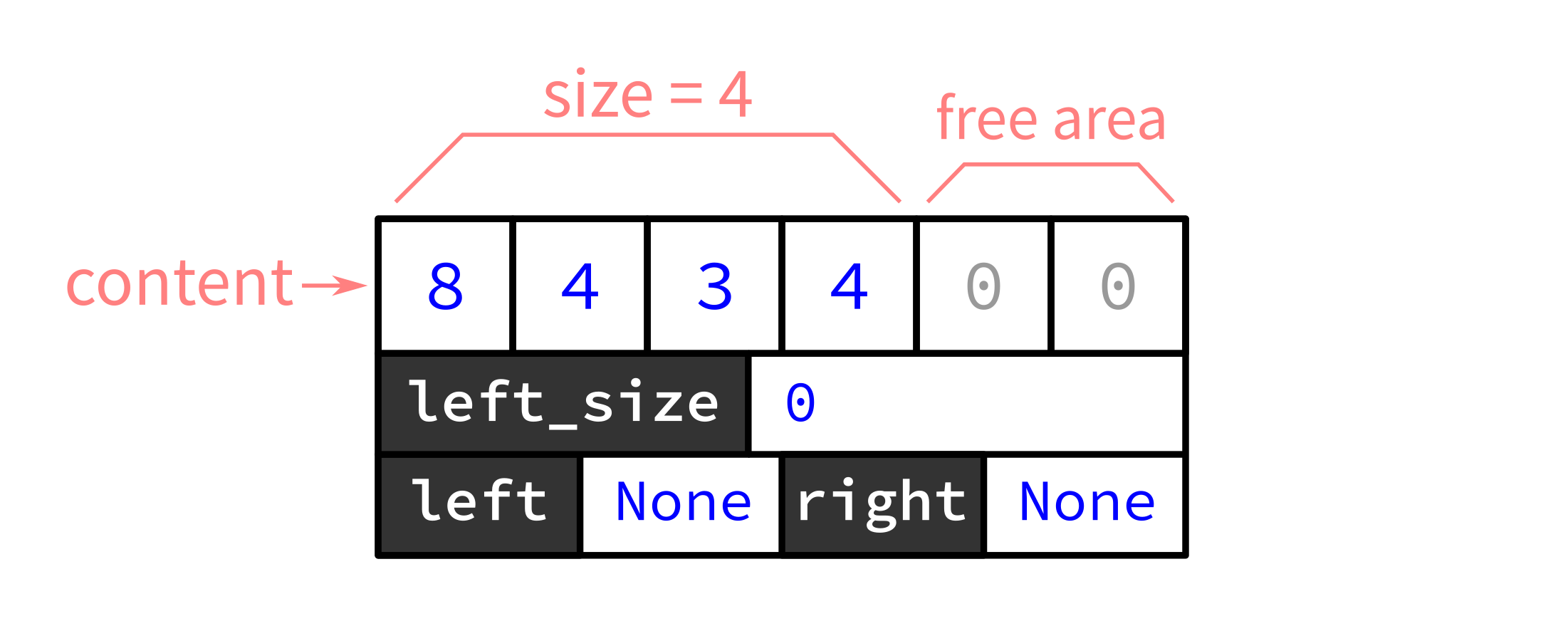
These BlockNode objects are not used individually but in a tree structure. Each node stores a chunk (contiguous sublist) of the data in content[:size], i.e. in the first size elements of its 6-integer storage area content. The left subtree contains chunks that appear earlier than this one in the data, while the right subtree contains chunks that appear later in the data. That means you can recover the data by doing an inorder traversal of the tree and joining up all the content[:size] lists in the order you encounter them.

For example, this tree stores the data [2,7,5,2,0,2,4,85,73,67,3,15]:

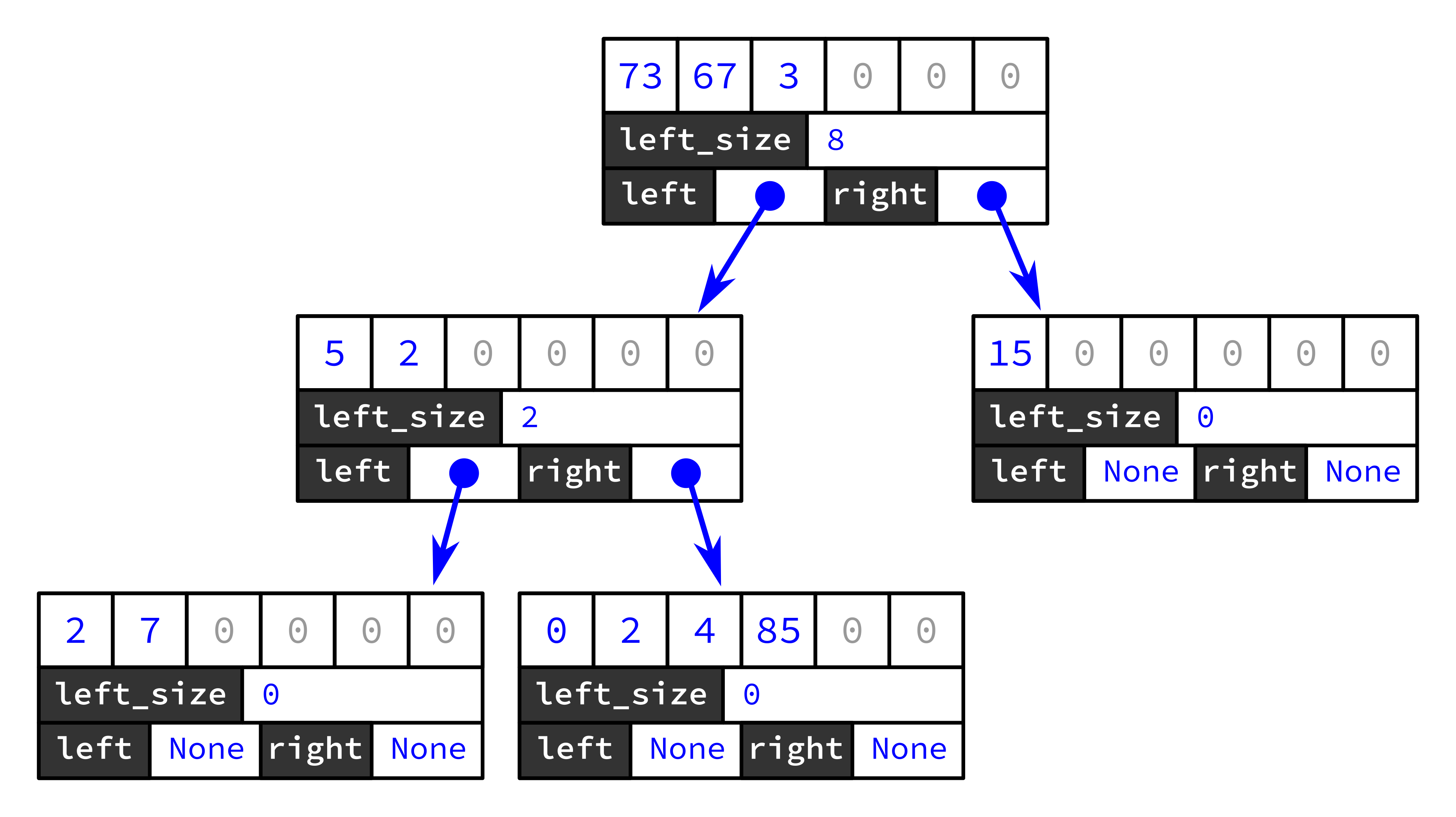
And inorder traversal of the tree recovers that sequence:

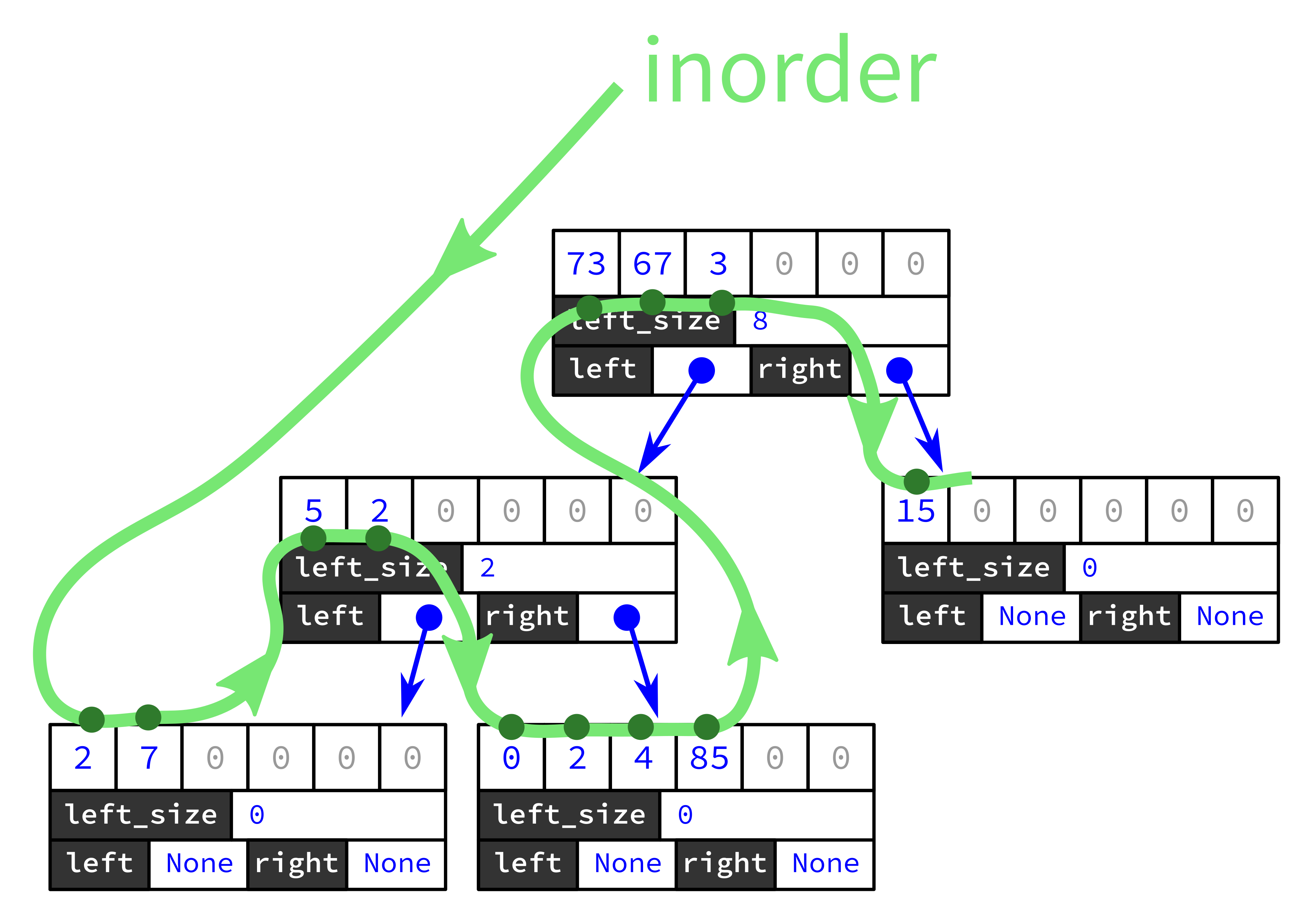
Of course there are a lot of ways to represent a given set of data by a tree. Here's another tree storing the same data, [2,7,5,2,0,2,4,85,73,67,3,15]:

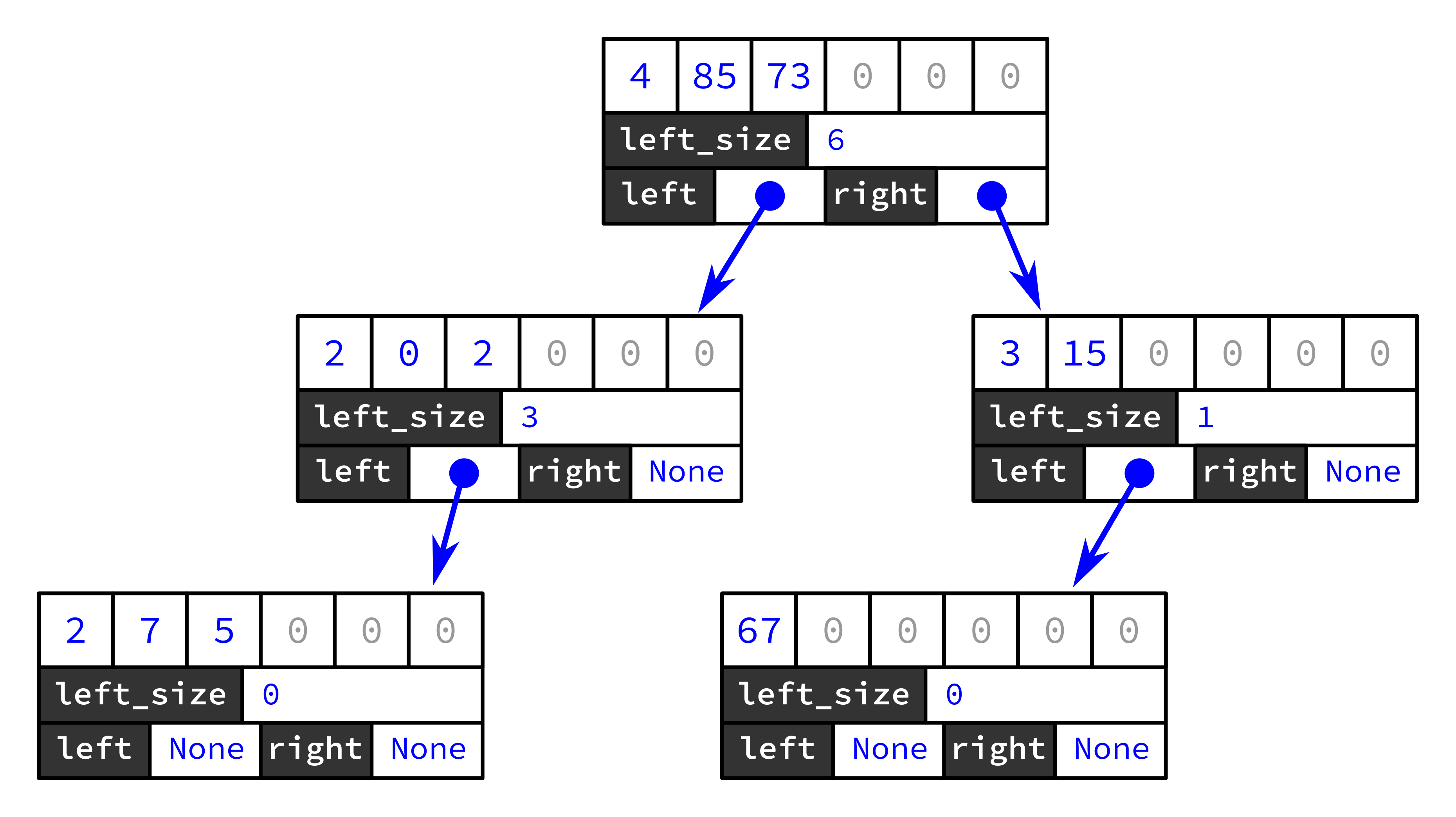
As you'll see in the method descriptions below, you'll need to find ways to insert or retrieve an integer at a given index using this structure. Here's a demonstration of how it is designed to make that possible. When you look at the tree above, we see that the integer 85 is stored in one of the slots of content in the root node. But what index does this correspond to in the data? It might seem like we need to examine all the nodes in the left subtree to determine this, since they all contain chunks of data that appear before the ones at the root node. But remember each node (including this one, the root) contains a left_size attribute that tells us exactly how many data elements are in the left subtree. Since that is 6 in this case, it means that the three integers stored at this node are indices 6, 7, and 8. Thus the integer 85 is content[1] for the root node and corresponds to data[7] (if we imagine data as a hypothetical list soring the same sequence of integers).

Similarly, every item in the tree has both a data index (its position in the data stored in the tree) and a content index (its position in the content attribute of the node it lies in). Neither type of index is stored directly; they are computed as needed by methods of BlockNode using the left_size attributes. Here is a diagram showing both types of indices for each item in the tree above:

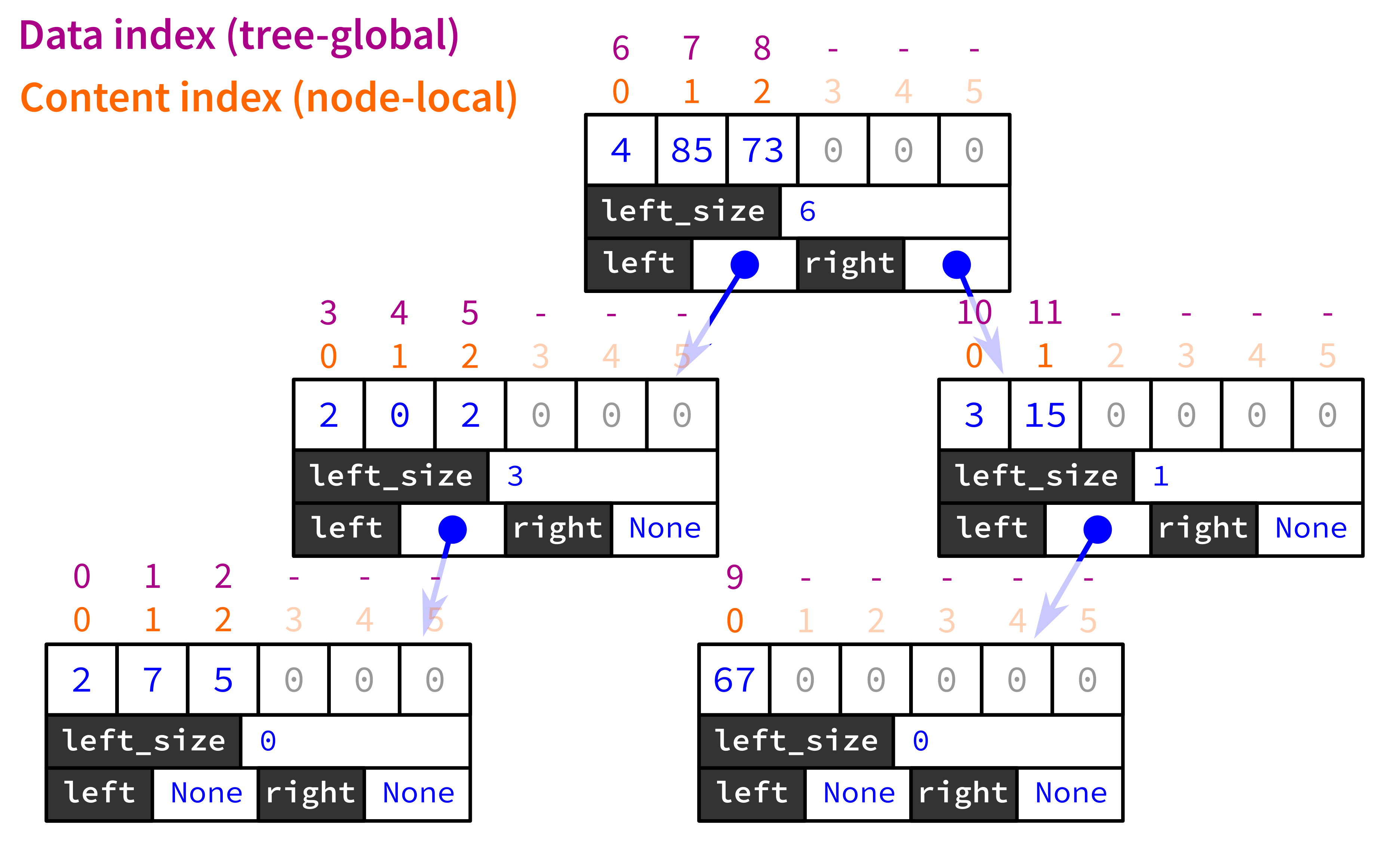
Methods¶

Class BlockNode must have the following methods. Feel free to define other methods (e.g. helper methods) if you find it useful to do so.

In describing methods, we omit the implicit self argument and just write it method the way it would be called.

There is no need to check arguments for type or validity unless it is specifically noted below.

• __init__(initial_content=None)

  • Arguments: initial_content is optional, but if given is assumed to be a list of at most 6 integers.
  • Behavior: Initializes the instance attributes described above. Once this is done, attribute content will never be assigned to a different list object, nor will its length ever change. The only allowable change to content is item assignment (e.g. self.content[0] = 41 puts 41 at position 0). If optional argument initial_content is not None, then it is expected to be a list of integers of length no more than 6. After performing other initialization, the constructor will copy the integers from initial_content into the first len(initial_content) indices of the instance attribute content, and then set the size attribute accordingly.

• set_left(node)

  • Arguments: node is either None or is a BlockNode instance.
  • Behavior: Sets instance attribute left to the value of argument node. If node is different from None, it must be a BlockNode object. In that case node.parent is set to self. (Thus, this is very similar to Node.set_left from trees.py, except it allows passing None as an argument.)

• set_right(node)

  • Arguments: node is either None or is a BlockNode instance.
  • Behavior: Sets instance attribute right to the value of argument node. If node is different from None, it must be a BlockNode object. In that case node.parent is set to self. (Thus, this is very similar to Node.set_right from trees.py, except it allows passing None as an argument.)

• __getitem__(idx)

  • Arguments: idx is a nonnegative integer less than or equal to the current length of the data.
  • Argument checking required: If idx is an integer outside the allowed range, an exception of type IndexError must be raised. The type of idx need not be checked.
  • Behavior: Search this node and the tree below it for the integer corresponding to index idx in the data, then return the result (an integer).
  • Notes:
    • Remember, this is a method you define and use but it is not meant to be called directly. The only time you write __getitem__ in your code is when defining this method. To call it, you don't write A.__getitem__(k) but instead use the equivalent but preferred syntax A[k].

• insert(idx,x)

  • Arguments: idx is a nonnegative integer less than or equal to the current length of the data. x is an integer.
  • Argument checking required: If idx is an integer outside the allowed range, raises IndexError. The type of idx need not be checked.

  • Behavior (REVISED CONTENT): Modify this tree of BlockNode objects to represent the result of inserting x at data index idx (shifting data indices of everything at or after that place right by one). Note that data index idx may be in this node or some other node.

    • This is easy if index idx corresponds to a spot in a BlockNode that has 5 or fewer integers from the data stored in it. However, if idx falls at a node that is "full", then some more work is required. The restrictions listed below basically say that this should be done in a "minimally invasive" way.
    • Important restriction 1 - If the node containing data index idx is not full, then no new nodes can be created.
    • Important restriction 2 - If the node containing data index idx is full, you are allowed to create up to two new nodes.
    • Important restriction 3 - You may need to modify the node containing data index idx, its ancestors, and its children, but the rest of the tree must not change.
    • Important restriction 4 - Under appropriate circumstances, it must be possible for this method to result in a node having two children. (If this were not the case, it would be building a list, not a tree.)

  • Advice: See the next subsection for discussion.

• is_full()

  • Arguments: No arguments.
  • Behavior: Returns a boolean indicating whether or not this node is full of data. That is, returns True if attribute size is equal to 6, and False otherwise.

• __len__()

  • Arguments: No arguments.
  • Behavior: Returns the total size of the data stored in this tree (i.e. the sum of size attributes of all nodes). Should take advantage of the fact that the sum of the sizes of the nodes in the left subtree is already known (rather than visiting them all needlessly).

• depth()

  • Arguments: No arguments.
  • Behavior: Returns the depth of the tree, meaning the length of the longest descending path starting at this node.

• append(x)

  • Arguments: x is an integer.
  • Behavior: Adds x to the end of the data by calling the method insert(n,x) where n is the current length of the data (i.e. the return value of __len__) before x is added.

• nodes()

  • Arguments: No arguments.
  • Behavior: Returns the number of nodes in the tree.

About node insertion¶

The method insert is the most complex one to write. Let's discuss the idea a bit. Suppose you have a BlockNode tree where the data item at index 15 is the integer 100, and the node A containing that integer full (meaning that node already contains 6 data items). If insert(15,999) is called, then we can't simply put 999 into A.content attribute of that node because there would be no room for the displaced item 100 in that node.

Now, we might be able to make room by bumping the the first or last item in A.content to another node. However, we can't use just any node; it would need to be the node that comes immediately after or before A in the inorder traversal of the tree, so the order of the data is preserved. Locating that node is somewhat complex---it may not be a child of A for example---and could easily run afoul of the rule that only A, its children, and its ancestors can be modified.

Instead, you should add a new empty node between A and one of its children in such a way that the new node is forced to come immediately after or immediately before A in the inorder traversal. Then, you can push some of the content from A to this new node, so that both A and the new node have some free space, while preserving the order of the data. (In fact, it's best to do this in a way that moves half of the data out of A, so we have two half-full nodes instead of one completely-full one.)

The Program¶

⚠ The autograder will only perform basic checks on this program. It will be reviewed for correctness during the manual grading step. ⚠

Create a script called bstoredemo.py that demonstrates and tests the class BlockNode by doing the following things (in the order listed):

1. Report on small scale randomly added data¶

Make a new BlockNode and then insert a random integer between 0 and 9 inclusive repeatedly until there are a total of 20 integers in the tree. Each time, the next integer should be inserted at an index selected at random from the ones that are valid at that time (i.e. the first one must be at index 0, the next one could be a index 0 or 1, the next at 0, 1, or 2, etc.).

Use the random module to make the random choices described above.

After each item insertion, print a short report about the state of the tree in the format shown below. The report will look a bit different each time, of course, and even if you use the same data as the example below, your tree may be different from the one my program generated. (As discussed before, many valid trees can represent the same data.)

data=[2]
Tree stats: nodes=1 depth=1 root_data=[2]

data=[1, 2]
Tree stats: nodes=1 depth=1 root_data=[1, 2]

data=[1, 2, 9]
Tree stats: nodes=1 depth=1 root_data=[1, 2, 9]

data=[1, 2, 9, 0]
Tree stats: nodes=1 depth=1 root_data=[1, 2, 9, 0]

data=[1, 2, 1, 9, 0]
Tree stats: nodes=1 depth=1 root_data=[1, 2, 1, 9, 0]

data=[1, 2, 1, 9, 6, 0]
Tree stats: nodes=1 depth=1 root_data=[1, 2, 1, 9, 6, 0]

data=[1, 1, 2, 1, 9, 6, 0]
Tree stats: nodes=2 depth=2 root_data=[9, 6, 0]

data=[1, 1, 4, 2, 1, 9, 6, 0]
Tree stats: nodes=2 depth=2 root_data=[9, 6, 0]

data=[1, 1, 4, 2, 1, 9, 6, 0, 4]
Tree stats: nodes=2 depth=2 root_data=[9, 6, 0, 4]

data=[1, 1, 4, 3, 2, 1, 9, 6, 0, 4]
Tree stats: nodes=2 depth=2 root_data=[9, 6, 0, 4]

data=[1, 3, 1, 4, 3, 2, 1, 9, 6, 0, 4]
Tree stats: nodes=3 depth=3 root_data=[9, 6, 0, 4]

data=[1, 3, 1, 4, 3, 6, 2, 1, 9, 6, 0, 4]
Tree stats: nodes=3 depth=3 root_data=[9, 6, 0, 4]

data=[1, 3, 1, 4, 3, 6, 2, 1, 6, 9, 6, 0, 4]
Tree stats: nodes=3 depth=3 root_data=[6, 9, 6, 0, 4]

data=[1, 3, 1, 4, 3, 6, 2, 1, 6, 9, 6, 0, 4, 5]
Tree stats: nodes=3 depth=3 root_data=[6, 9, 6, 0, 4, 5]

data=[1, 3, 1, 4, 3, 6, 7, 2, 1, 6, 9, 6, 0, 4, 5]
Tree stats: nodes=3 depth=3 root_data=[6, 9, 6, 0, 4, 5]

data=[1, 3, 0, 1, 4, 3, 6, 7, 2, 1, 6, 9, 6, 0, 4, 5]
Tree stats: nodes=3 depth=3 root_data=[6, 9, 6, 0, 4, 5]

data=[1, 3, 0, 1, 4, 3, 6, 7, 2, 1, 6, 9, 6, 0, 2, 4, 5]
Tree stats: nodes=4 depth=3 root_data=[6, 9, 6]

data=[1, 3, 0, 1, 4, 3, 6, 7, 2, 1, 6, 9, 6, 9, 0, 2, 4, 5]
Tree stats: nodes=4 depth=3 root_data=[6, 9, 6, 9]

data=[1, 3, 0, 1, 4, 3, 8, 6, 7, 2, 1, 6, 9, 6, 9, 0, 2, 4, 5]
Tree stats: nodes=4 depth=3 root_data=[6, 9, 6, 9]

data=[1, 3, 0, 1, 4, 3, 8, 6, 7, 2, 1, 6, 9, 6, 9, 0, 2, 4, 5, 7]
Tree stats: nodes=4 depth=3 root_data=[6, 9, 6, 9]

Hint: Because BlockNode supports both __len__ and __getitem__, Python can automatically convert it to a list of all the data just by calling list(T) where T is the root node.

2. Correctness test¶

Make an empty BlockNode called T and an empty list called L.

Then, do the following 10,000 (ten thousand) times using a loop:

• Select a random integer x in the range 0 to 999 inclusive.
• Select a random integer idx in the range 0 to len(L) inclusive. (NOTE CORRECTED RANGE!)
• Insert x into L at index idx
• Insert x into T at index idx
• Confirm that L[i] and T[i] are equal for all valid indices i.

Note that L and the tree with root T keep growing throughout this process. You don't reset or empty them after each iteration. At the end you have a list and a tree each containing 10,000 items and it has been confirmed that they behaved the same (in terms of __getitem__) at every stage of construction.

If all goes well, this step produces no output except printing

Correctness test with 10,000 items: OK

But if anything goes wrong inside the loop, an exception should be raised that ends the program.

3. Time test¶

Make two lists of length 100,000 (one hundred thousand):

• A list data of random integers in the range 0 to 999 inclusive.
• A list indices of random integers so that indices[k] is between 0 and k inclusive.

Using these two lists, do two tests:

First, make an empty list L and then for each i in range(100_000) insert data[i] into L at index indices[i]. Measure the total amount of time it takes to do this and print it in this format:

LIST insert time test: 0.63 seconds

Second, make an empty BlockNode called T and then for each i in range(100_000) insert data[i] into T at index indices[i]. Measure the total amount of time it takes to do this and print it in this format:

TREE insert time test: 1.77 seconds

In each case the time is printed with two digits after the decimal point.

Note: You will probably find BlockNode to be slower than List, i.e. the fancier data structure "loses" the timing contest. But if you increased the number of integers to a few tens of millions, then BlockNode would probably start to be faster (i.e. to "win").

IMPORTANT RULES YOUR CODE MUST FOLLOW¶

Your project must follow the rules in the MCS 275 coding standards document. In addition:

• Only submit bstore.py and bstoredemo.py - The autograder will supply everything else.

• No replacement of content attributes - Once a BlockNode is created, the attribtue content should remain as the same 6-element list object forever. The items in the list may change, but the attribute itself should never be assigned a different value. That is:

  • In a method of BlockNode, writing self.content[k] = x is OK
  • In a method of BlockNode, writing self.content = ... is FORBIDDEN except when the attribute is first created in the constructor.

• Make proper use of trees - Your BlockNode class must have the ability to build trees where an arbitrary number of nodes have both left and right children. Without this, you really have just a list of nodes, not a proper tree.

• Make proper use of structured programming - Have methods call one another when appropriate, rather than having lots of duplicated or near-duplicate code.

• No use of float except to store elapsed time - No values of type float can be created or used in bstore.py. In bstoredemo.py, the only float values that are permitted are those used to compute elapsed time.

• Methods of BlockNode should never make a list of the entire data - A silly way to do some of the things requested would be to convert the entire tree of nodes into a huge list of all the data, then do something with that list to complete the task. This is analogous to converting a binary tree to a list instead of using a proper search algorithm---it is wasteful and unnecessary. Always make proper use of the tree structure to do the things requested.

• Reasonable efficiency - The autograder will allow up to 5 seconds for each test case in bstore.py to run, and will let bstoredemo.py run for up to 25 seconds. If the time limit is reached without the test being completed, no points will be given. I strongly suggest you avoid worrying about the time it takes to do things UNLESS you have a working program that is failing tests solely because of taking too long. Most likely this will never be an issue, and tests that fail because of a timeout will only occur if your code has a genuine bug that causes it to be stuck in an infinite loop or other process that will never finish.

Appendix: How to test without insert (NEW CONTENT)¶

Nothing in this section is strictly required to complete the project. Use it if it is helpful, ignore it if is not.

If you have a BlockNode class that has a constructor and instance attributes, but you haven't yet made the insert method, you might wonder how to test __getitem__ and other methods.

The recommended strategy is to make a tree of BlockNode objects "manually", setting content, size, left_size, left, right, and parent of each node manually. Then you can test out the behavior of __len__, __getitem__, etc., using a tree that you understand.

Below you will find two examples of trees shown as diagrams and code to build them starting from a BlockNode class that only has a constructor with the right instance attributes.

Manual construction example 1¶

Here is the tree:

The data it stores is:

The following code constructs it in a variable named A without using insert.

Manual construction example 2¶

Here is the tree:

The data it stores is:

The following code constructs it in a variable named A without using insert.

How your project will be graded¶

Autograder: 30 points¶

The autograder tests the bstore.py module and grades it based on its behavior. Limited checks of bstoredemo.py will also run, but they won't meaningfully verify its correctness.

Manual review: 20 points¶

I will test bstoredemo.py for correctness and evaluate this on a scale of 0 to 10 points. The autograder's checks of that program will be limited.

Then I will award the remaining 10 points based on adherence to the coding standards and other rules given above, and a review of your methods of solving the problem. If I see that your program does not do what was requested in this document, but the error was not detected in the automated testing, a deduction may be given at this point. The scores assigned by the autograder will not be changed during manual review unless I discover some kind of intentional wrongdoing (such as an attempt to circumvent or reverse-engineer the autograder's operation).

Revision history¶

• 2024-03-05 Initial publication
• 2024-03-10 Revise insert description to clarify existing requirements and to prevent solutions that violate the spirit of the assignment (e.g. "trees" that are actually just lists, or a tree of nodes that each store a single item)
• 2024-03-10 Add appendix about manual tree construction
• 2024-03-13 Range of index should be 0 to len(L) inclusive in the correctness test. (Was off by one.)