MCS 275 Spring 2024 Worksheet 9 Solutions¶
- Course instructor: Emily Dumas
- Emily Dumas, Kylash Viswanathan, Patrick Ward
Topics¶
This worksheet is about numpy (and gives a bit of additional practice with pillow). In lecture we used Julia sets as a sample application for numpy. We may return to that topic in worksheet 10 but for now we'll focus on some other numpy fundamentals.
Resources¶
These things might be helpful while working on the problems. Remember that for worksheets, we don't strictly limit what resources you can consult, so these are only suggestions.
- Lecture 21 - numpy 1
- Lecture 22 - numpy 2
- Lecture 23 - Julia sets
- VanderPlas:
- Chapter 2 covers numpy
-
- Especially /numpy_matplotlib/
- MCS 260 course materials from Fall 2021:
Browser-based notebook strongly recommended¶
I think you'll have the best experience with this worksheet if you do your work in a Python notebook environment based in your web browser. That means either:
- Jupyter (which you install with
python3 -m pip install notebookand run withpython3 -m notebook) - Google Colab to make and use notebooks on a remote computer
Also, remember to install numpy (and pillow, if you haven't already). For most people thse commands will do it:
python3 -m pip install numpy
python3 -m pip install pillow
1. Generate these arrays¶
Try to find concise expressions that generate these numpy arrays, without using explicit loops and without listing all the elements out as literals.
A.¶
array([ 4, 9, 16, 25, 36, 49, 64, 81, 100, 121])B.¶
array([ 0.2, 0.4, 0.6, -5. , -5. , -5. , -5. , -5. , 1.8, 2. , 2.2, 2.4, 2.6, 2.8, 3. , 3.2, 3.4, 3.6])C.¶
array([[4., 3., 2., 1., 0., 1., 2., 3., 4.],
[4., 3., 2., 1., 0., 1., 2., 3., 4.],
[4., 3., 2., 1., 0., 1., 2., 3., 4.],
[4., 3., 2., 1., 0., 1., 2., 3., 4.],
[4., 3., 2., 1., 0., 1., 2., 3., 4.],
[4., 3., 2., 1., 0., 1., 2., 3., 4.],
[4., 3., 2., 1., 0., 1., 2., 3., 4.]])D.¶
array([[7, 0, 7, 7, 7, 7, 7, 7, 0, 7],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[7, 0, 7, 7, 7, 7, 7, 7, 0, 7],
[7, 0, 7, 7, 7, 7, 7, 7, 0, 7],
[7, 0, 7, 7, 7, 7, 7, 7, 0, 7],
[7, 0, 7, 7, 7, 7, 7, 7, 0, 7],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
[7, 0, 7, 7, 7, 7, 7, 7, 0, 7]])Solution¶
A.¶
import numpy as np
A = np.arange(2,12)**2
A
B.¶
B = np.arange(0.2,3.8,0.2)
B[3:8] = -5
B
C.¶
C = np.abs(np.zeros((7,9)) + np.arange(-4,5))
C
D.¶
D = np.full((8,10),7,dtype="int64")
D[1]=0
D[-2]=0
D[:,1]=0
D[:,-2]=0
D
2. Numpy image processing¶
Here is a grayscale photograph of a wall in the Red Fort, a 16th century fort in the city of Agra, India.
Link to the file: ws9-red-fort.png
Directory where you can find it on github: worksheets/images/
The image itself (which you may be able to right-click and "save as"):

In this problem, you'll work with the data from this image using numpy. Last week, you did some image processing using .getpixel and .putpixel from Pillow, but converting the image to a numpy array and then analyzing the data using numpy is a much better approach (meaning it's faster and more flexible).
Here are two functions that will help with that: One loads a PNG image into a numpy array. It requires numpy and PIL. If the PNG image is grayscale, you'll get a 2-dimensional array whose dtype is uint8. The other saves a 2-dimension numpy array with dtype uint8 as a PNG image.
import PIL.Image
import numpy as np
def load_image_to_array(fn):
"Open image file with name `fn` and return as a numpy array`"
img = PIL.Image.open(fn)
return np.array(img)
def save_array_to_image(fn,A):
"Save 2D array `A` with dtype `uint8` to file named `fn`"
assert A.ndim == 2
assert A.dtype == np.dtype("uint8")
img = PIL.Image.fromarray(A)
img.save(fn)
A. Extrema¶
What row of the image has the largest average brightness? (Is it the only one, or are there ties?)
What column has the largest average brightness? (Again, uniquely so?)
What is the brightest color that appears in the image? Where does it appear?
Solution¶
import numpy as np
import os
os.chdir("images")
# load the image, and obtain the dimensions.
from PIL import Image
fort = load_image_to_array("ws9-red-fort.png")
row_means = np.mean(fort, axis = 1) #obtains the means of the rows
np.argmax(row_means) #returns the row with the highest brightness
col_means = np.mean(fort, axis = 0) # obtains the means of the columns
np.argmax(col_means)
# Obtain index of maximium value
# The index returned is an integer, giving the position
# of the maximum in the 1D array obtained by joining
# all the rows together, one after another
max_idx = np.argmax(fort)
# Obtain the corresponding row and column
# Each row has fort.shape[1] items, so the number of times
# this divides max_idx will be the row number.
max_row = max_idx // fort.shape[1] # each row has fort.shape[1] items
# Each row has fort.shape[1] items, so the remainder when
# dividing max_idx by that will be the column number.
max_col = max_idx % fort.shape[1]
print("Indices of brightest color", max_row,max_col)
print("Brightest color", fort[max_row][max_col])
# Confirm that this is the true maximum
# Using .ravel() which reshapes an ND array to 1D
# (we didn't cover this function, and you don't need to know about it)
assert fort[max_row][max_col] == fort.ravel()[max_idx]
B. Horizontal average¶
Create a new grayscale image file red-fort-colavg.png with the same dimensions as the original image, but where each column is filled with a solid color that is as close as possible to the average brightness of the coresponding column of the original image. That means the result will look like a bunch of gray vertical lines of varying brightness.
Hint: If you have an array of floats you can convert them to an array of uint8 values using the method call .astype("uint8").
Solution¶
fort_colavg = (np.zeros_like(fort) + np.mean(fort,axis=0)).astype("uint8")
save_array_to_image("ws9_grayscale_fort_colavg.png",fort_colavg)
Here's the result.
PIL.Image.fromarray(fort_colavg)
C. Vertical average¶
Create a new grayscale image file red-fort-rowavg.png with the same dimensions as the original image, but where each row is filled with a solid color that is as close as possible to the average brightness of the coresponding row of the original image. That means the result will look like a bunch of gray horizontal lines of varying brightness.
Solution¶
fort_rowavg = ((np.zeros_like(fort) + np.mean(fort,axis=1)).T).astype("uint8")
save_array_to_image("ws9_grayscale_fort_rowavg.png",fort_rowavg)
Here's the result.
PIL.Image.fromarray(fort_rowavg)
D. Gamma adjust¶
If you divide a grayscale image array by $255.0$, you get an array of floats between $0.0$ and $1.0$. If you raise those floats to a power $\gamma$ (usually chosen to be near $1$) and then multiply by $255.0$ again, the resulting image will be "gamma adjusted" by exponent $\gamma$. Of course if $\gamma=1$ you just get the original image back again.
Apply this process to the photo with for each of these values of $\gamma$:
- 0.25
- 0.7
- 1.0
- 1.2
- 1.4
- 2
- 5
How would you explain the qualitative effect of changing $\gamma$?
Solution¶
As $\gamma$ increases, the brightness decreases and as $\gamma$ decreases, the brightness increases. The resulting images are shown below.
To make the image sizes manageable in the solution notebook, we scale them down by a factor of 3. To create full-size versions, remove the [::3,::3] below.
fort_scaled = fort[::3,::3]
gamma = 0.25
PIL.Image.fromarray((((fort_scaled/255.0)**gamma)*255.0).astype("uint8"))
gamma = 0.7
PIL.Image.fromarray((((fort_scaled/255.0)**gamma)*255.0).astype("uint8"))
gamma = 1.0
PIL.Image.fromarray((((fort_scaled/255.0)**gamma)*255.0).astype("uint8"))
gamma = 1.2
PIL.Image.fromarray((((fort_scaled/255.0)**gamma)*255.0).astype("uint8"))
gamma = 1.4
PIL.Image.fromarray((((fort_scaled/255.0)**gamma)*255.0).astype("uint8"))
gamma = 2
PIL.Image.fromarray((((fort_scaled/255.0)**gamma)*255.0).astype("uint8"))
gamma = 5
PIL.Image.fromarray((((fort_scaled/255.0)**gamma)*255.0).astype("uint8"))
3. Riemann Sum¶
The area under one "hump" of the sine function is exactly 2, i.e. $$ \int_0^\pi \sin(x) \, dx = 2 $$
For any positive integer n, that integral can be approximated by dividing the interval $[0,\pi]$ into n equal parts and forming a left-endpoint Riemann sum, whereby the area is approximated by a union of n rectangles. This is shown below for n=12:
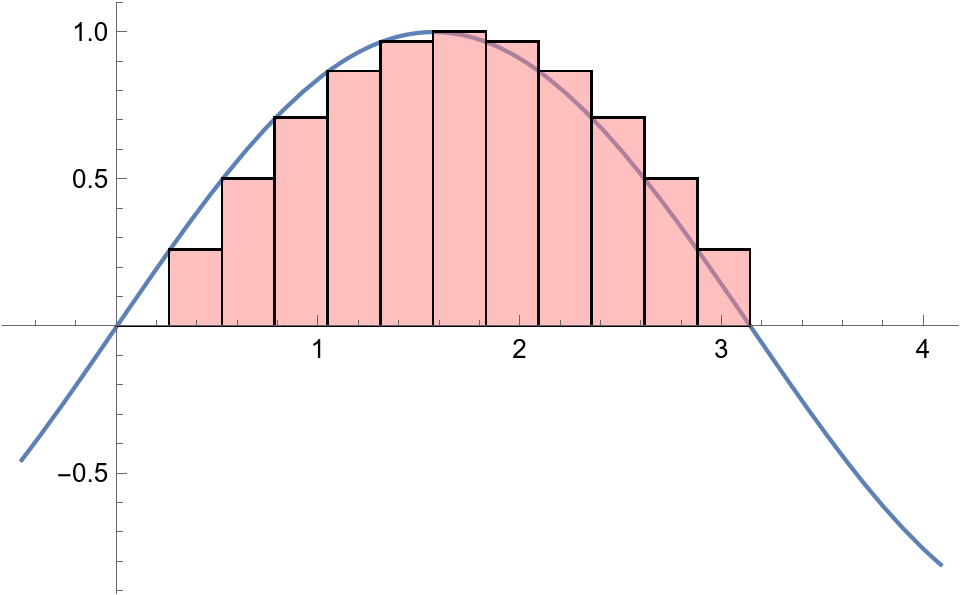
Here's a function that computes the Riemann sum naively, using Python for loops:
import math
def naive_rs(n):
"""
Riemann sum for sin(x) on [0,pi] computed without numpy
and without any concern for accumulating errors when you
sum many small floats. (TODO: Learn numerical analysis!)
"""
hsum = 0.0
for i in range(n):
hsum += math.sin(math.pi*(i/n)) # Add a rectangle height
return hsum * (math.pi/n) # Multiply sum of heights by width
As we can see, the return value gets quite close to 2 as we increase n.
naive_rs(3)
naive_rs(5)
naive_rs(5_000_000)
However, for large values of n this function is quite slow. (Try n=5_000_000 or n=20_000_000 for example.)
Write a function numpy_rs(n) that makes an equivalent computation using numpy to avoid explicit iteration.
Check that numpy_rs(n) and naive_rs(n) return values that are extremely close for small values of n. (They can't be expected to necessarily agree exactly, as floating point addition is not associative.)
Then compare the speed of numpy_rs(n) and naive_rs(n) for large values of n. (For this problem, let's say a value of n is "large" if the slower of the two calculations takes at least half a second.)
Hints: You won't need the math module at all in the numpy solution. There's a constant called np.pi that is equal to $\pi$.
The solution must not contain any Python loops.
Solution¶
def numpy_rs(n):
"Riemann sum for sin(x) on [0,pi] with numpy"
return np.sum(np.sin(np.pi*np.linspace(0,1,n+1)))*np.pi/n
# Implementation of numpy's integration via Riemann Sums
import time
t0 = time.time()
numpy_rs(5_000_000)
print(time.time()-t0)
# Implementation of numpy's integration via Riemann Sums
t0 = time.time()
naive_rs(5_000_000)
print(time.time()-t0)
The numpy version runs quite a bit faster!
Revision history¶
- 2023-03-04 - Initial publication