Lecture 12
Recursion
MCS 275 Spring 2021
Emily Dumas
Lecture 12: Recursion
Course bulletins:
- Quiz 4 due Tuesday at Noon CST
- Please complete anonymous feedback survey (link in Blackboard announcement)
Recursion
In computer science, recursion refers to a method of solving a problem that depends on solving smaller versions of the same problem.
Usually, recursion involves a function calling itself.
Strategies using recursion
- Divide and conquer: A problem can be split into pieces; solutions for the pieces can be combined to the full solution.
- e.g. Mergesort
- Decrease and conquer: Reduce a problem for a given input (e.g.
n) to the answer for a slightly smaller input (e.g.n-1) and a bit of extra work. - e.g. Factorial
Iteration
Recursive solutions are often contrasted with iterative solutions.
- Iterative: Loops and local variables keep track of all state (work to be done, work completed, next ...)
- Recursive: Arguments keep track of current state; call stack stores work in progress; return values send back results.
Recursive solutions can always be converted to iterative ones, often at the cost of more complex code.
Stop condition
A function that always calls itself will never finish!
Recursion must include some kind of stop condition---a case in which the function can directly return an answer instead of calling itself.
Today's examples
- Factorial
- Fibonacci numbers
- Paper folding sequence
Factorial
The classic first example of recursion, computing $$n! = n \times (n-1) \times \cdots \times 2 \times 1.$$
The argument to the function decreases with each subsequent call, so it eventually reaches the stop condition ($n \leq 1$).
Fibonacci
The Fibonacci numbers are defined by $$F_0=0,\; F_1=1,\; \text{and }F_n = F_{n-1} + F_{n-2}$$
So the sequence begins $0,1,1,2,3,5,8,13,...$
The definition immediately suggests a recursive implementation.
Paper folding sequence

Paper folding sequence
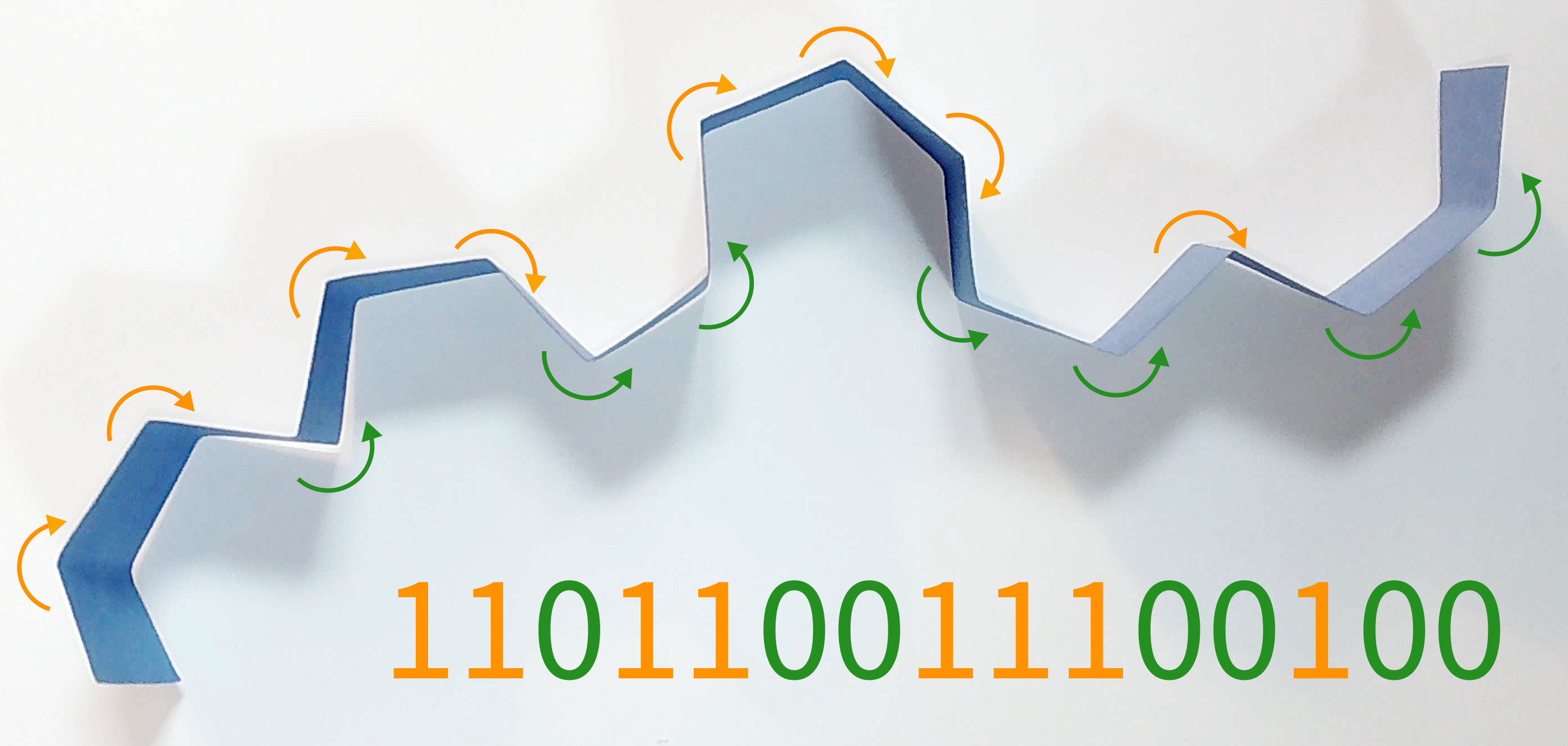
Paper folding sequence
Let $\oplus$ denote concatenation of binary sequences, so $0110 \oplus 11 = 011011$.
If $A$ is a binary sequence, let $\bar{A}$ denote the sequence with $0$ and $1$ switched, e.g. $\overline{11101} = 00010$
Finally, let $A^r$ denote the sequence in opposite order, e.g. $10010^r = 01001$.
$$PFS(n) = PFS(n-1) \oplus 1 \oplus \overline{PFS(n-1)^r}$$
References
- Lutz discusses recursive functions in Chapter 19 (pages 555-559 in the print edition).
- Intro to Python for Computer Science and Data Science by Deitel and Deitel discusses recursion in Chapter 11. The online version of this text is freely available to UIC students, faculty, and staff. (You will first need to log in with you UIC email.)
- The open textbook Think Python, 2ed, by Allen B. Downey discusses recursion in Sections 5.8 to 5.10.
- Computer Science: An Overview by Brookshear and Brylow discusses recursion in Section 5.5. (This book is often an optional text for MCS 260.)
- Lecture 12 of MCS 275 Spring 2021 discusses recursion.
Revision history
- 2021-02-08 Fixed value of $F_0$
- 2021-02-08 Initial publication