Lecture 10

Recursion vs Iteration II

MCS 275 Spring 2024
Emily Dumas

View as:   Presentation   ·   PDF-exportable  ·   Printable

Lecture 10: Recursion vs Iteration II

Reminders and announcements:

  • Project 1 due Fri Feb 9
  • Homework 4 coming Thursday afternoon

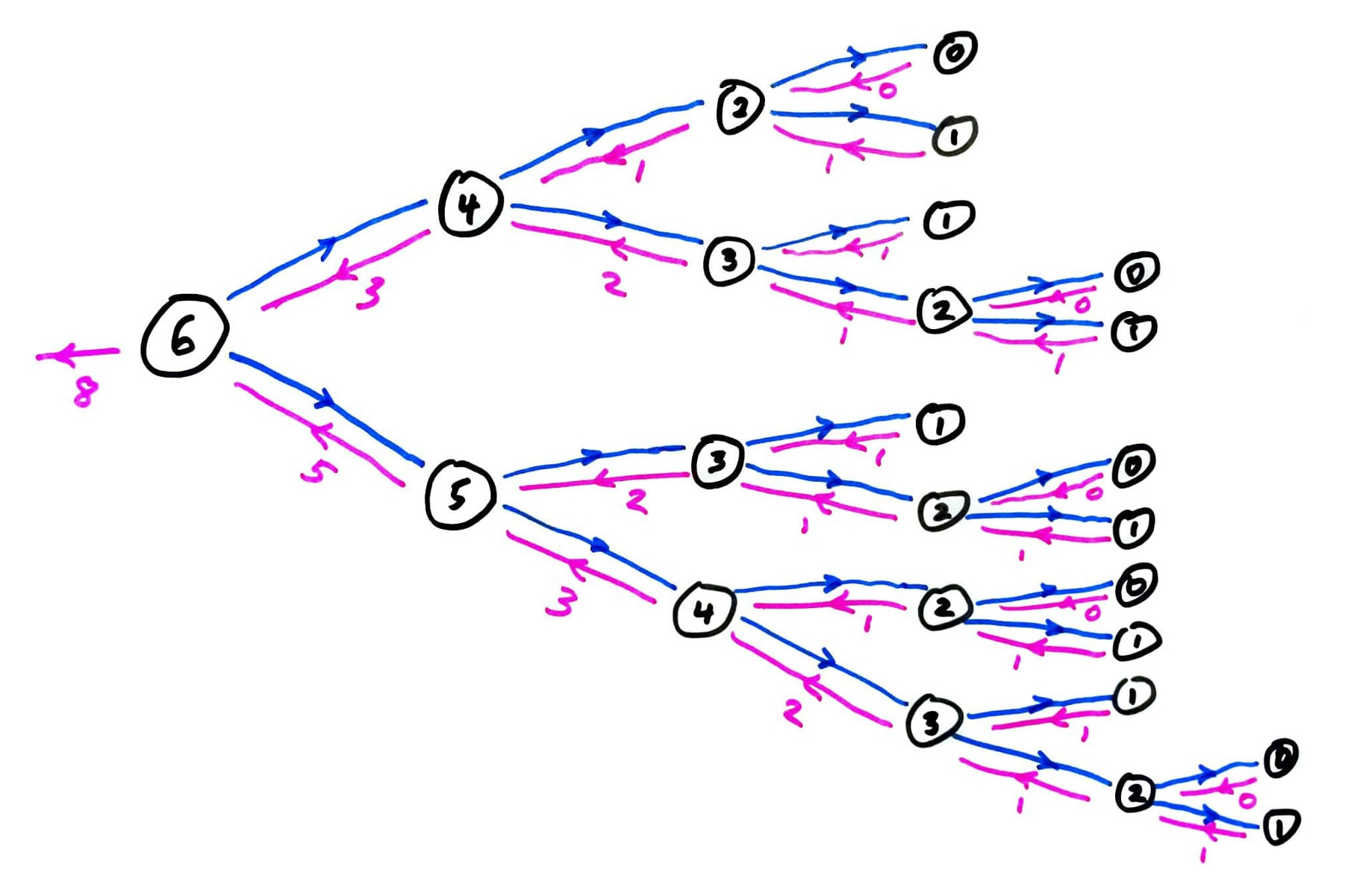
This is fib(6). Notice how many calls (e.g. fib(3)) happen multiple times? Each results in more recursion.

It's even worse for fib(n) with larger n.

Memoization

A technique to address this problem:

  1. Store the results of expensive calculations.
  2. Have subsequent calls retrieve stored answers instead of calculating.

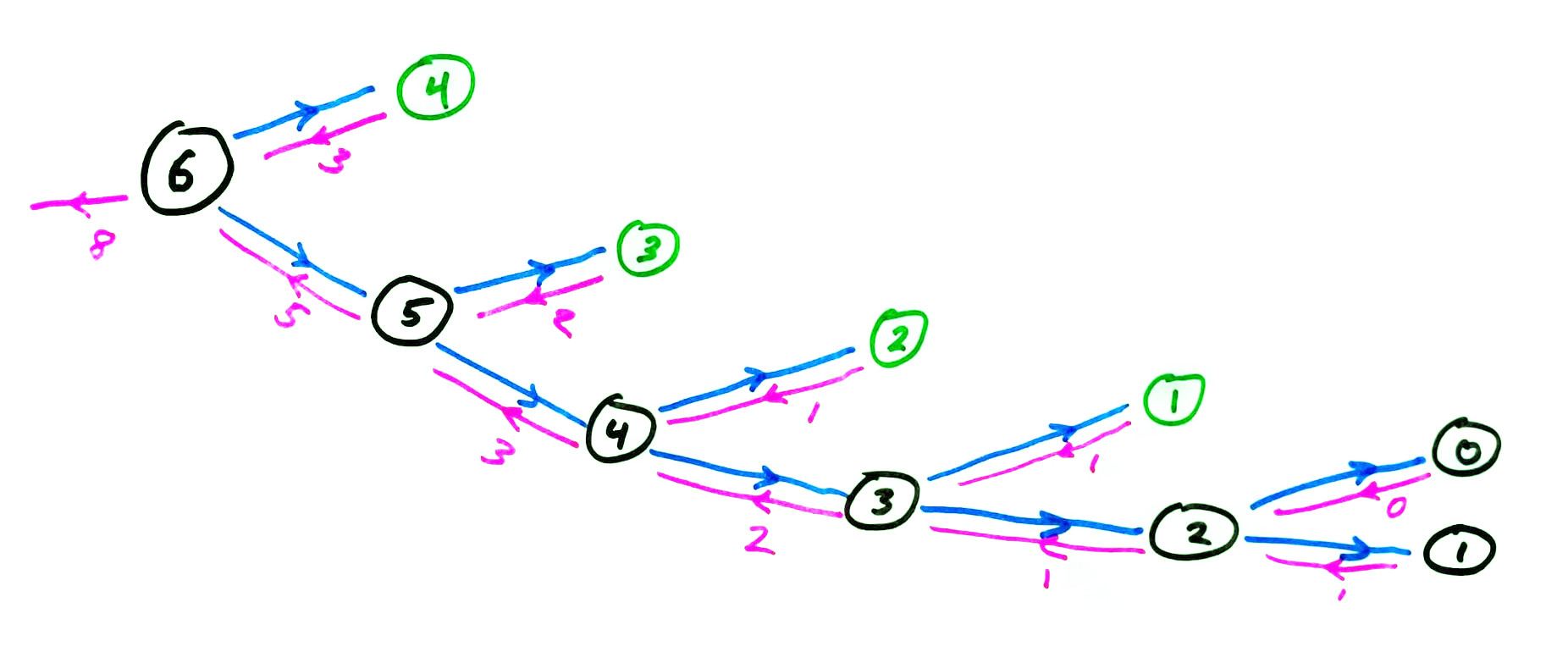
Let's memoize fib.

memoized fib call graph

memoized fib call graph

Fibonacci timing summary

n=35 n=450
recursive (naive) 1.9s ≫ age of universe
recursive (memoized) <0.001s 0.003s
iterative <0.001s 0.001s

Measured on my old office PC (2015, Intel i7-6700K) with Python 3.8.5

Call counts

Another way to measure the cost of a recursive function is to count how many times the function is called.

Let's do this for recursive fib.

$n$ 0 1 2 3 4 5 6
calls 1 1 3 5 9 15 25
$F_n$ 0 1 1 2 3 5 8 13
Theorem: Let $T(n)$ denote the total number of times fib is called to compute fib(n). Then $$T(0)=T(1)=1$$ and $$T(n) = T(n-1) + T(n-2) + 1.$$

Corollary: $T(n) = 2F_{n+1}-1$.

Proof of corollary: Both sequences $T(n)$ and $2F_{n+1}-1$ have the same first two terms, and obey the same recursion relation. Induction.

Corollary: $T(n) = 2F_{n+1}-1$.

Proof of corollary: Let $S(n) = 2F_{n+1}-1$. Then $S(0)=S(1)=1$, and $$\begin{split}S(n) &= 2F_{n+1}-1 = 2(F_{n} + F_{n-1}) - 1\\ &= (2 F_n - 1) + (2 F_{n-1}-1) + 1\\ & = S(n-1) + S(n-2) + 1\end{split}$$ Therefore $S$ and $T$ have the same first two terms, and follow the same recursive definition based on the two previous terms. By induction, the set of $n$ such that $T(n) = 2F_{n+1}-1$ is all of $\mathbb{N}$.

Corollary: Every time we increase $n$ by 1, the naive recursive fib does $\approx61.8\%$ more work.

(The ratio $F_{n+1}/F_n$ approaches $\frac{1 + \sqrt{5}}{2} \approx 1.61803$.)

Recursion with backtracking

How do you solve a maze?

Recursion with backtracking

How do you solve a maze?

My guess at your approach:

  • Follow a path with your eyes, choosing turns somewhat arbitrarily.
  • If you reach a dead end, go back a bit and reconsider.

A formal version of this recursion with backtracking. Start with

  • The maze
  • A path from the start to somewhere

Add one more step to the path.

Make a recursive call to see what happens after that.

If the answer is "nothing good", consider a different next step.

Backtracking

Two stop conditions: Dead end or goal.

If goal: Great! Return the path as solution.

If dead end: Return None to tell whoever called us to try something else (to backtrack).

Algorithm depth_first_maze_solution:

Input: a maze and a path under consideration (partial progress toward solution).

  1. If the path is a solution, just return it.
  2. Otherwise, enumerate possible next steps that don't go backwards.
  3. For each of the possible next steps:
    • Make a new path by adding this next step to the current one.
    • Make a recursive call to attempt to complete this path to a solution.
    • If recursive call returns a solution, we're done. Return it immediately.
    • (If recursive call returns None, continue the loop.)
  4. If we get to this point, every continuation of the path is a dead end. Return None.

Depth first

This method is also called a depth first search for a path through the maze.

Here, depth first means that we always add a new step to the path before considering any other changes (e.g. going back and modifying an earlier step).

Maze coordinates

Maze API

Let's explore the Maze class from maze.py.

References

Same suggested references as Lecture 9.

Revision history

  • 2023-02-08 Finalization of the 2023 lecture this was based on
  • 2024-01-30 Initial publication