Lecture 13
Divide and Conquer
Quicksort
MCS 275 Spring 2024
Emily Dumas
Lecture 13: Quicksort
Reminders and announcements:
- Project 1 due 11:59pm Friday
- Project 1 autograder open—expect multiple submit/debug cycles
- Project 2 (on recursion) coming on Monday
Transformation vs mutation
Last time we wrote a mergesort function that acts as a transformation: A list is given as input, a new sorted list is returned.
Another approach we could consider is sorting as a mutation: A list is provided, the function reorders its items and returns nothing.
In place
A sorting transformation necessarily uses a lot of additional memory when applied to a large list (e.g. to store the output).
A sort that operates as a mutation has the possibility of using only a small amount of memory to do its work.
Doing so is called an in place sorting method.
Quicksort
A recursive, in place sorting method that, like mergesort, is reasonably efficient and widely used.
Partition
Let's first study something weaker than sorting.
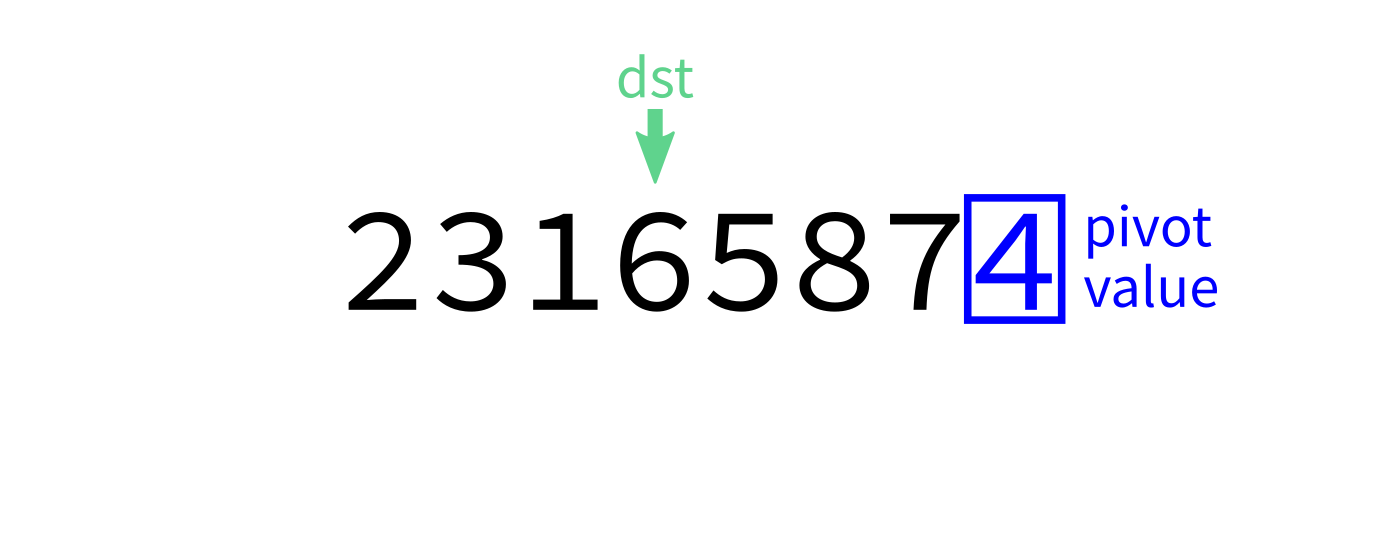
Suppose we have a list L and have chosen one of its elements, p.
We want to rearrange L so that it looks like:
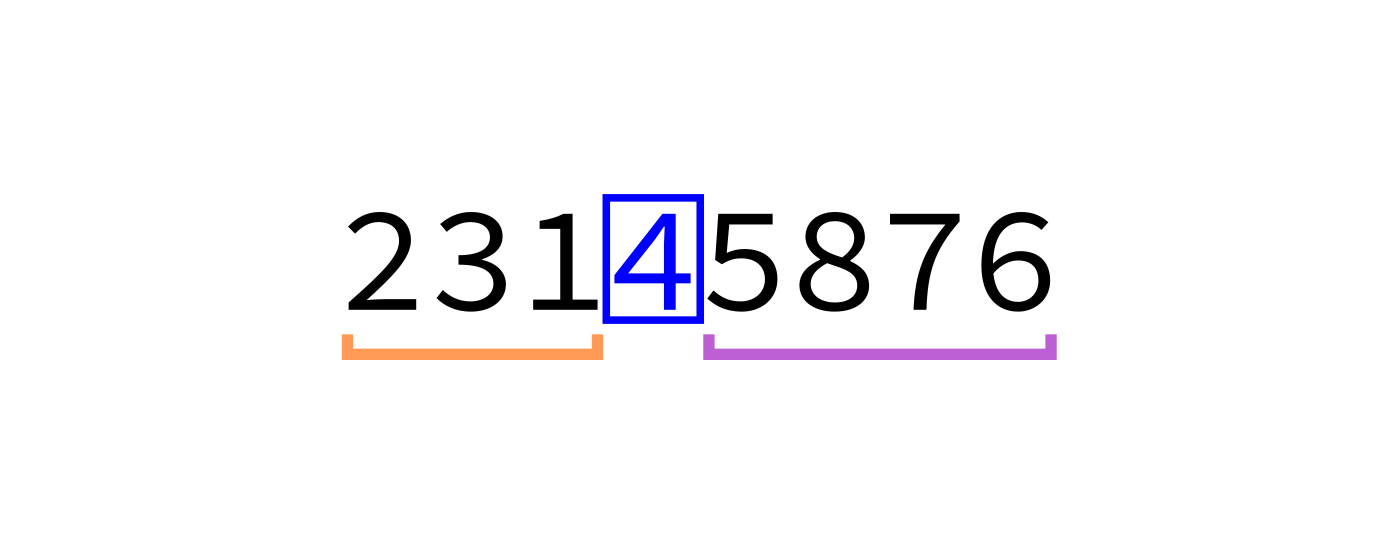
[ items < p, p, items ≥ p ]
We say L has been partitioned at p, and we call p the
pivot.
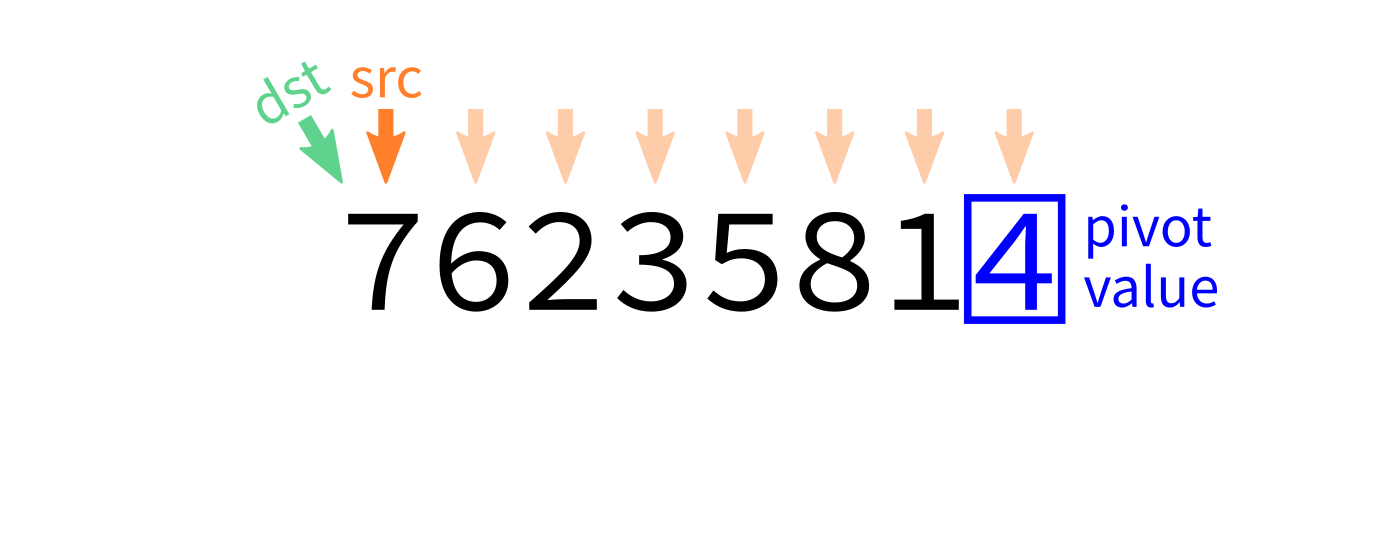
Partition algorithm idea
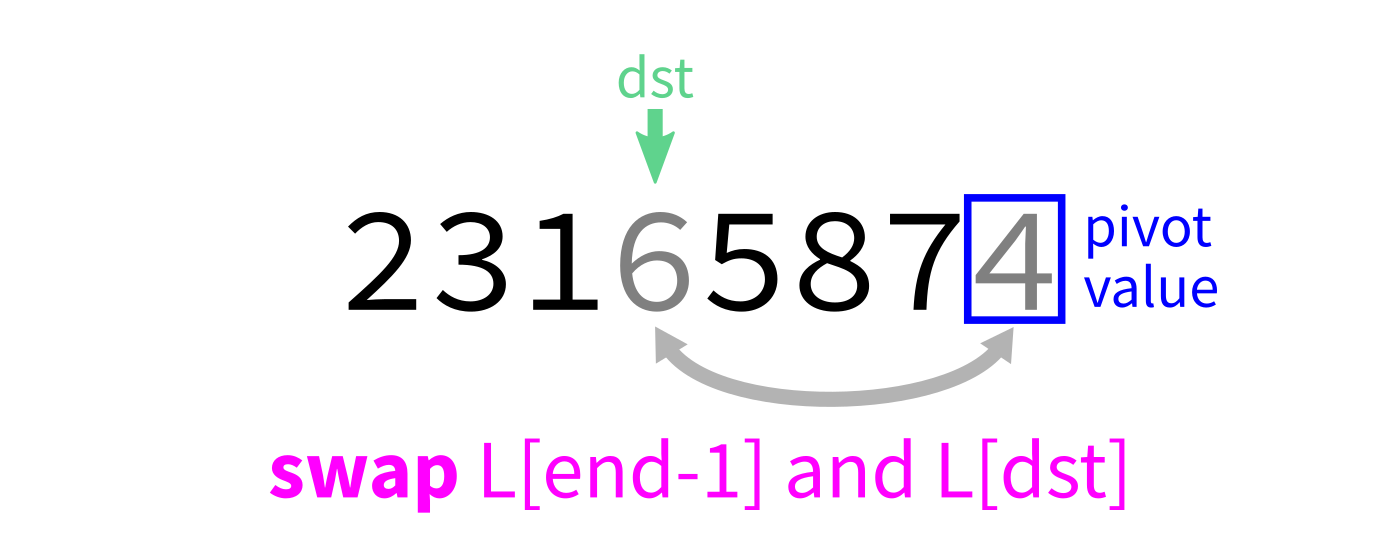
Scan through the list, moving things smaller than the pivot to the beginning.
It will be convenient to suppose p was the last element of L. In general we could move p there first if needed.
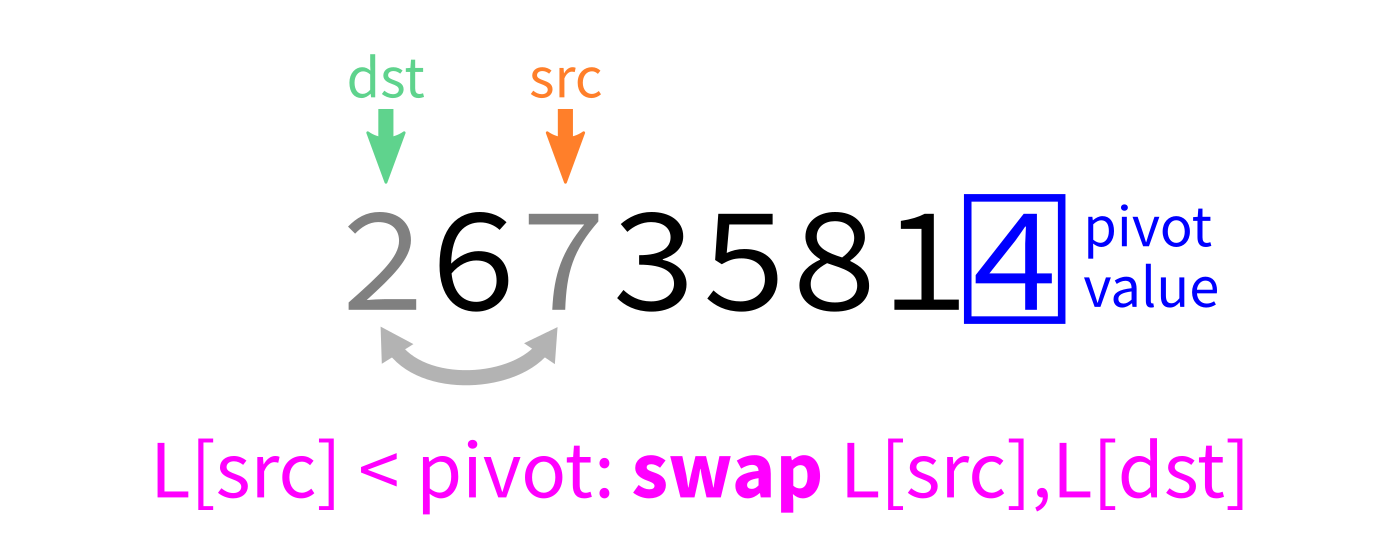
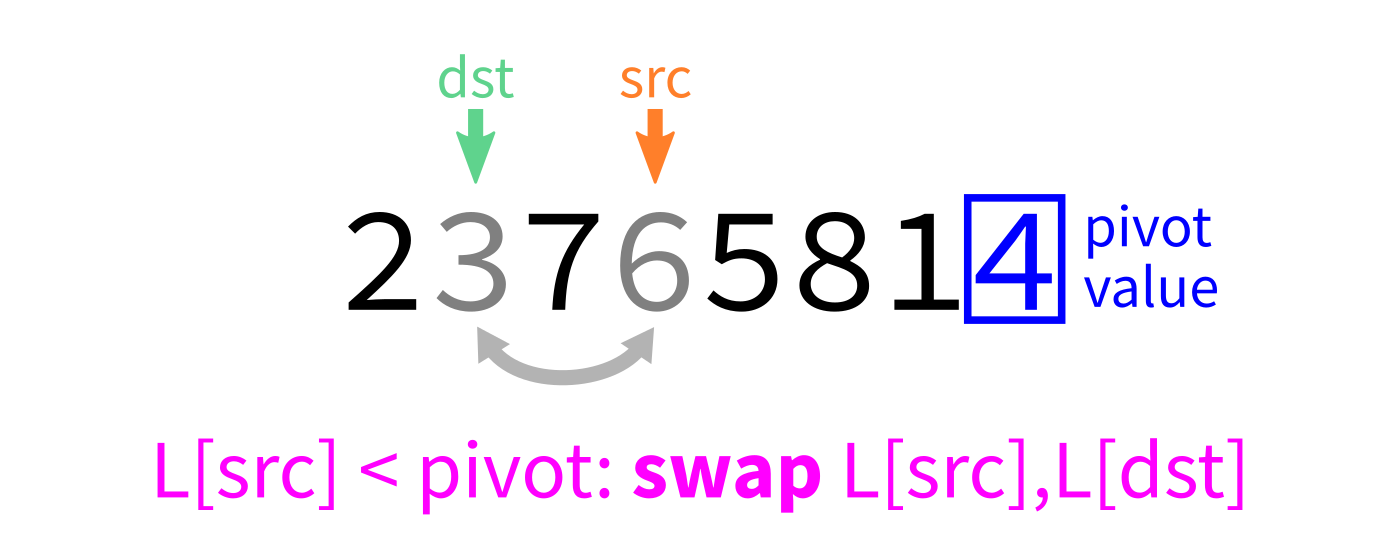
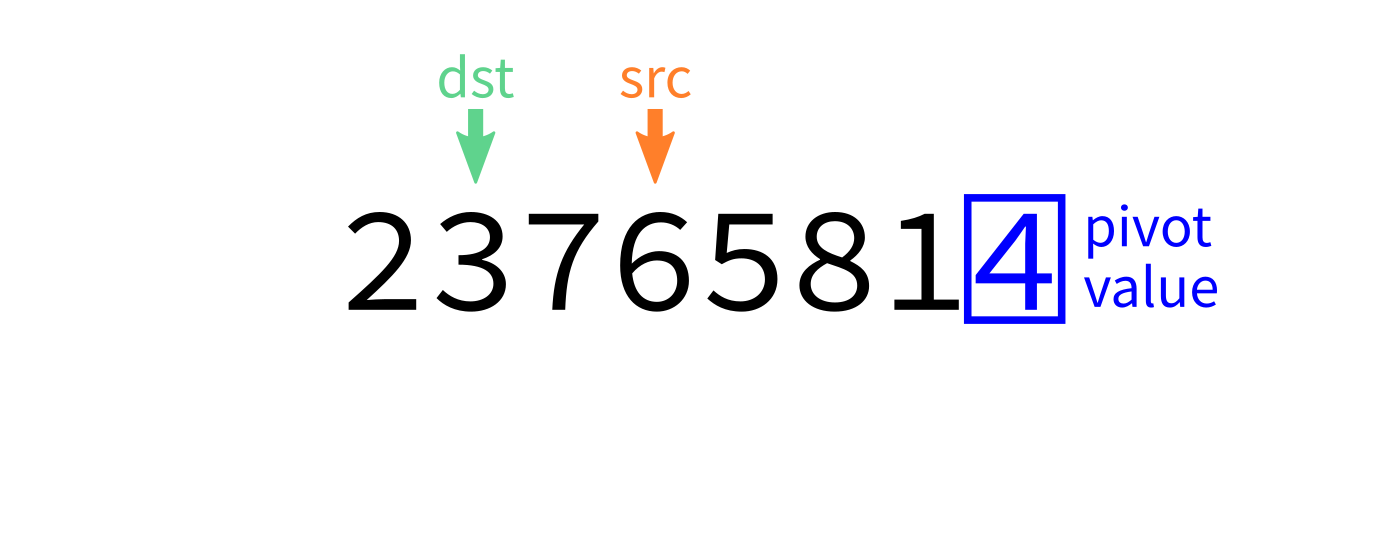
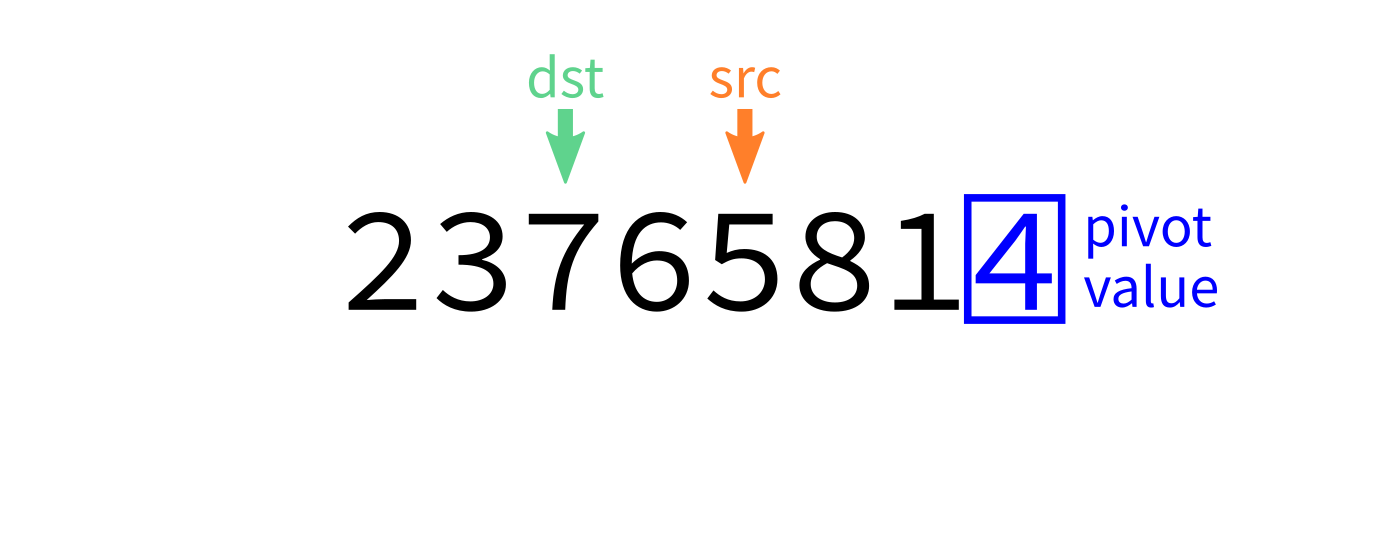
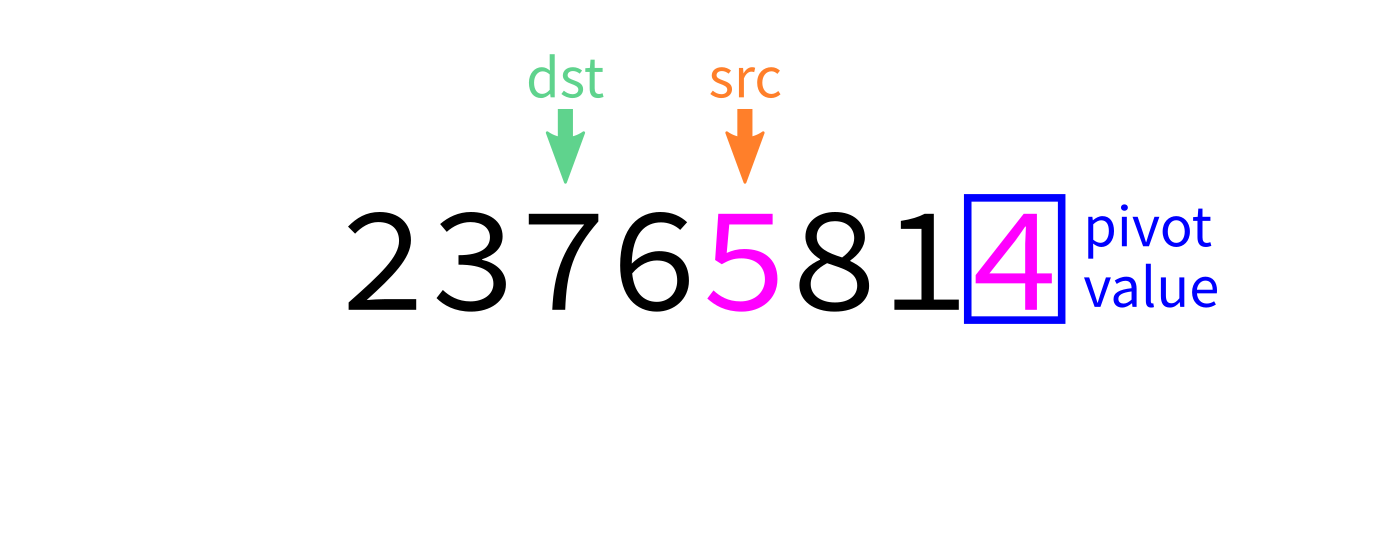
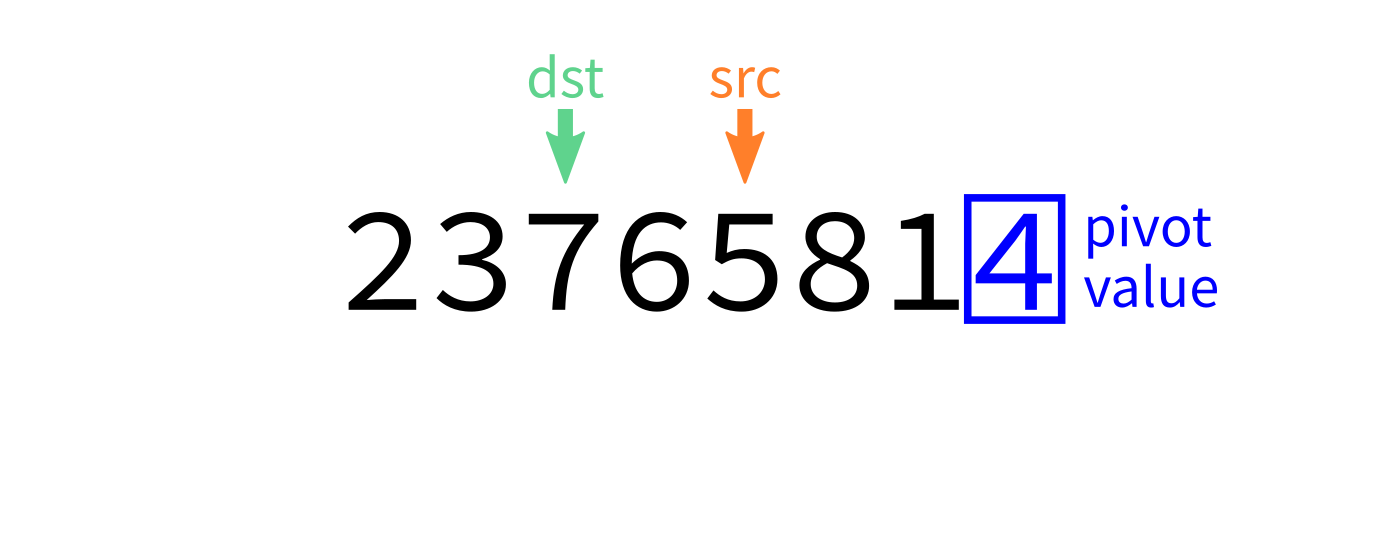
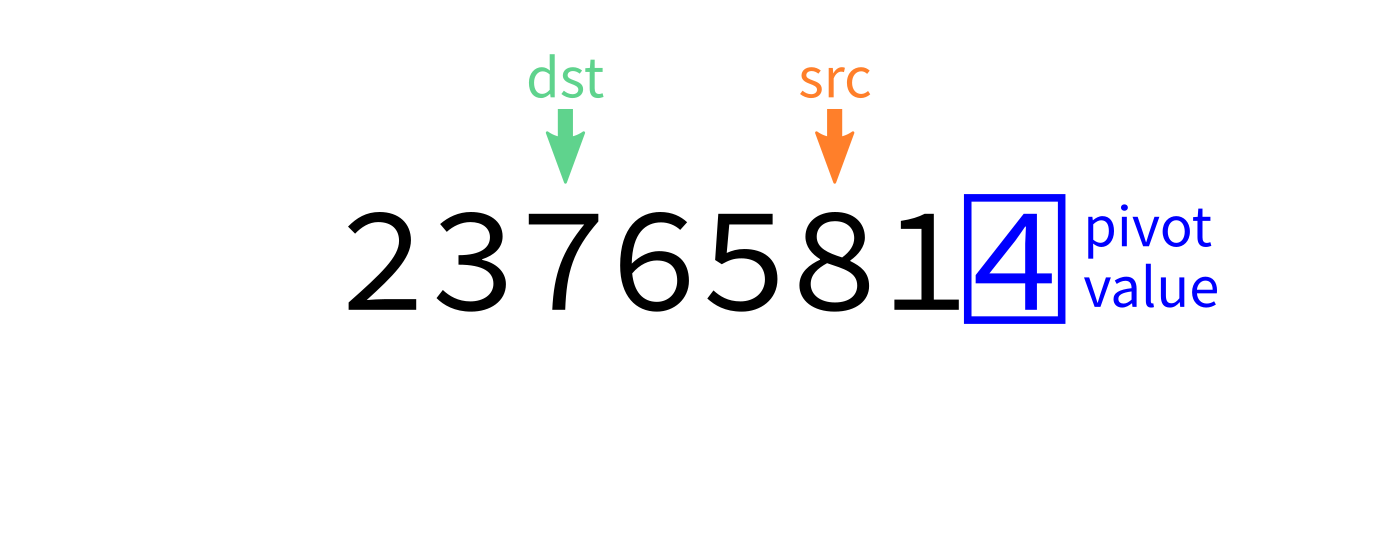
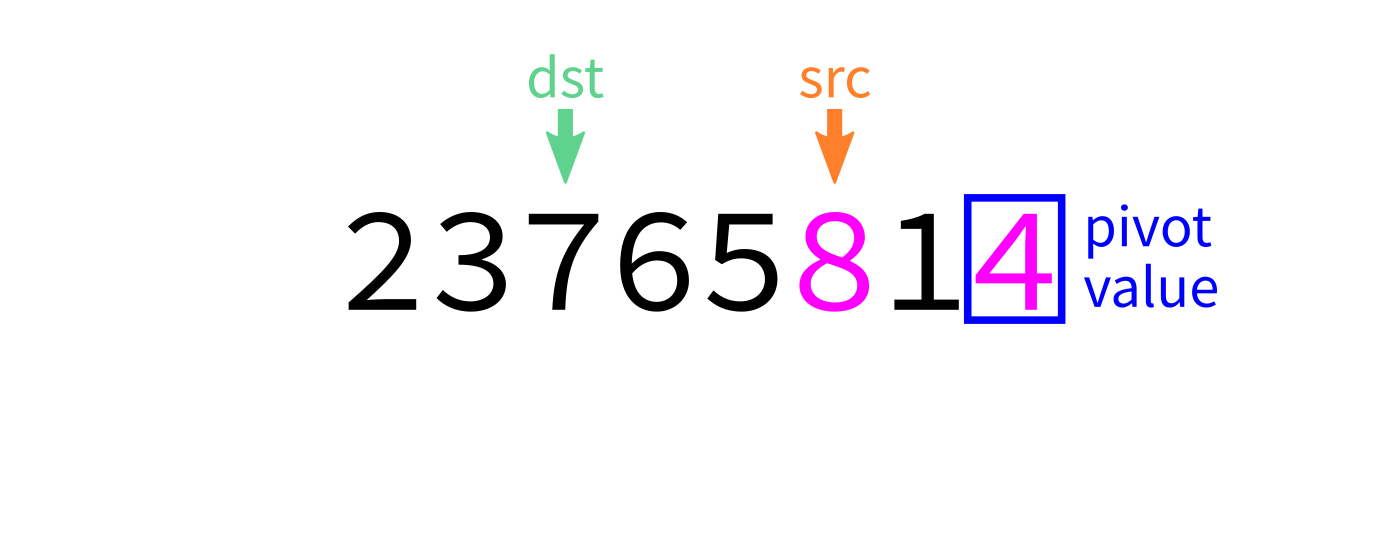
Partition algorithm visualization
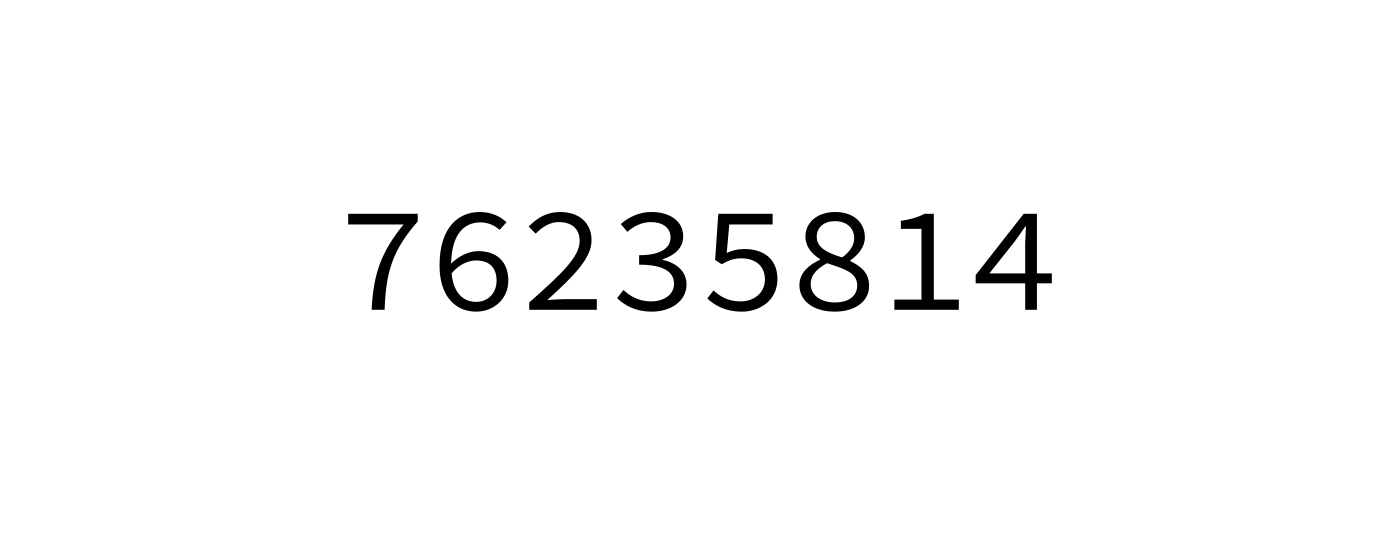

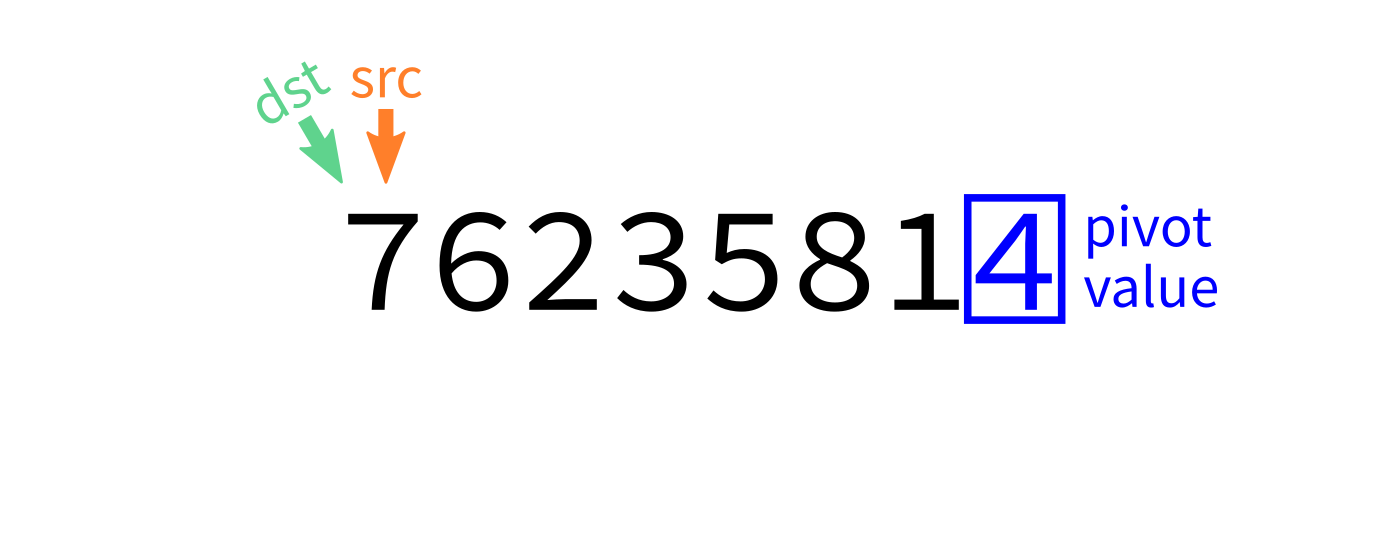
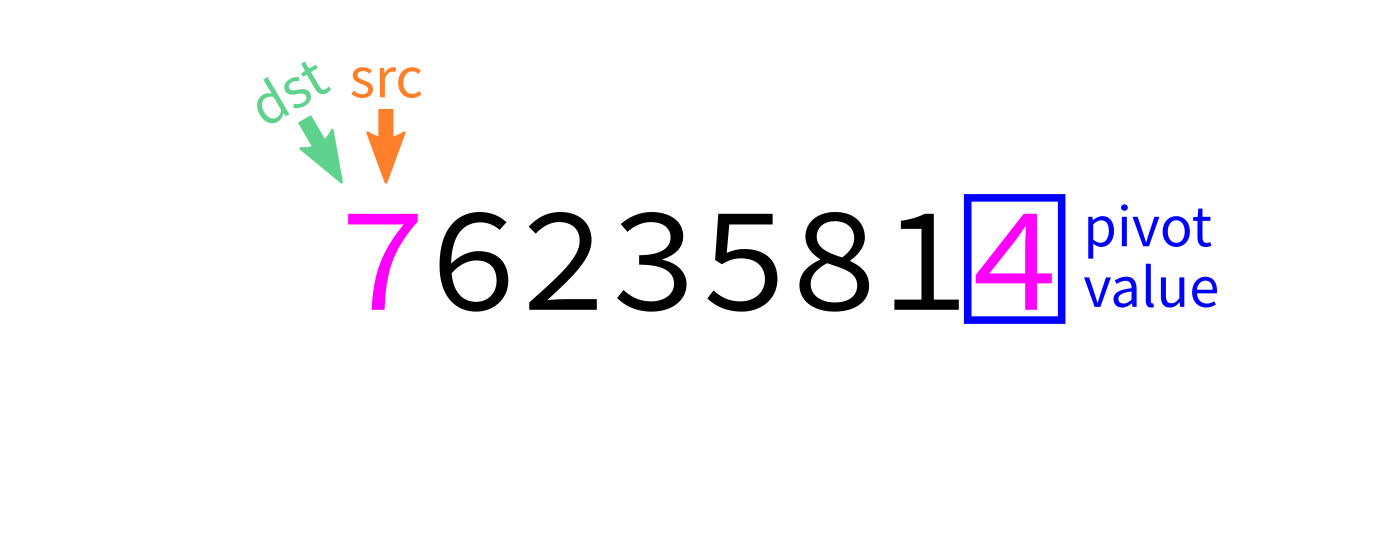
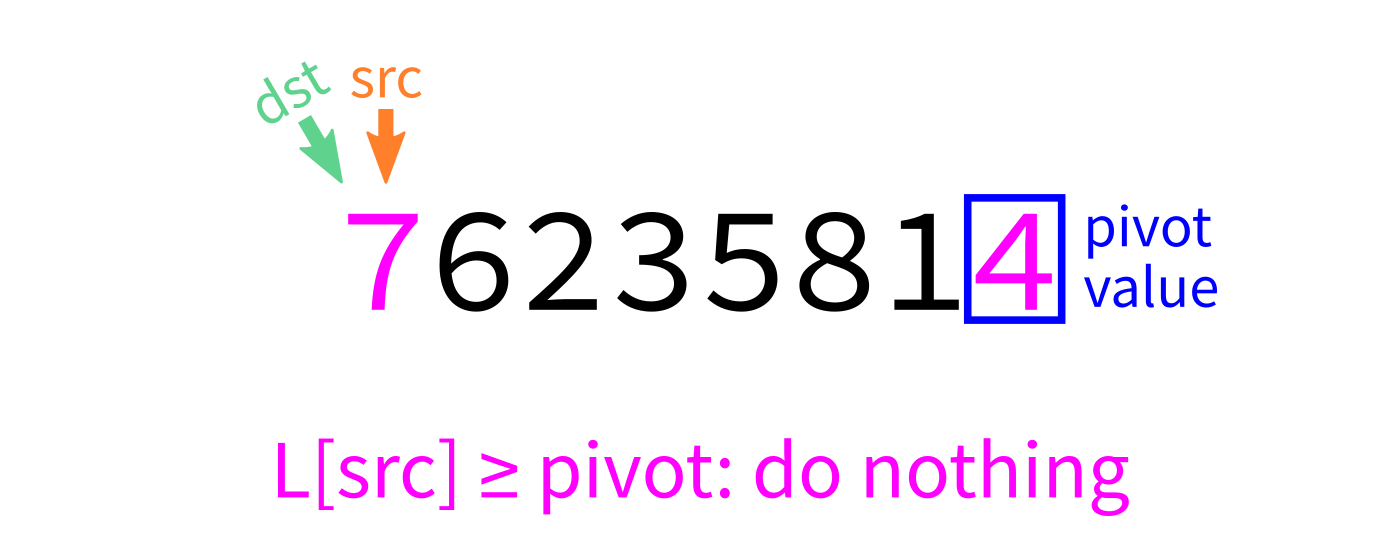
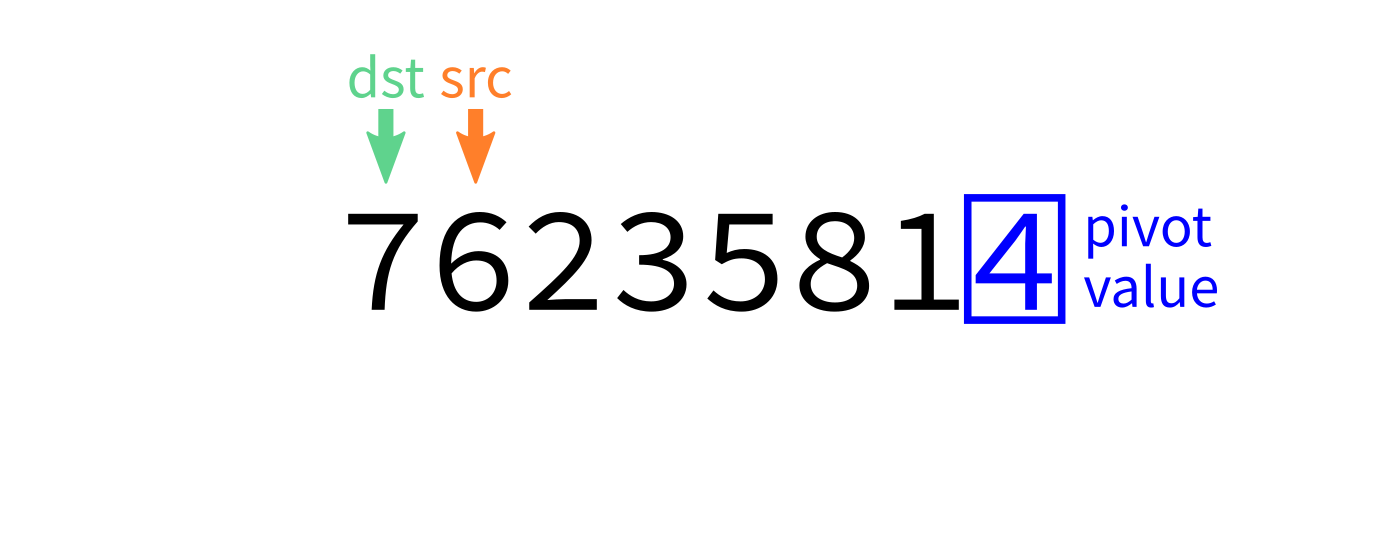
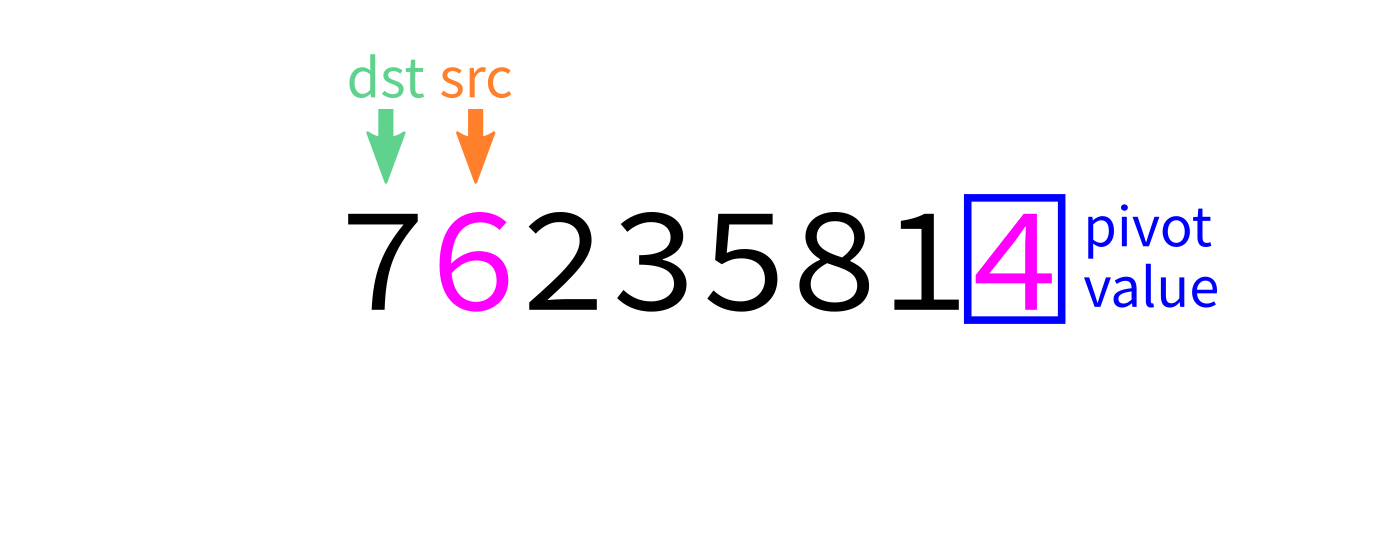
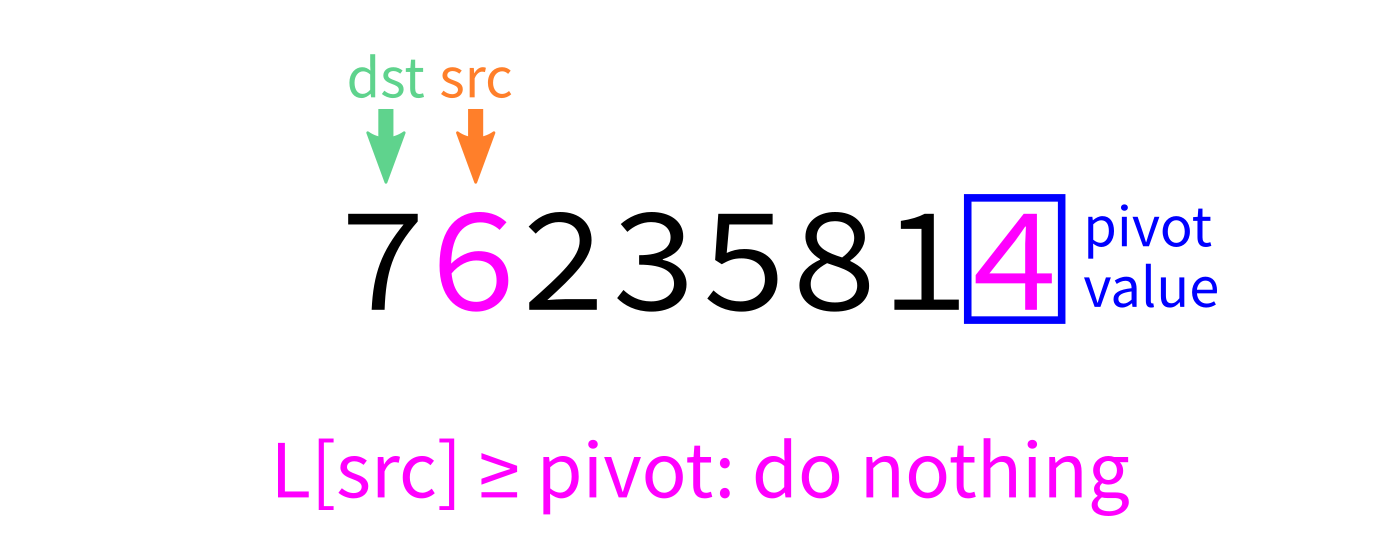
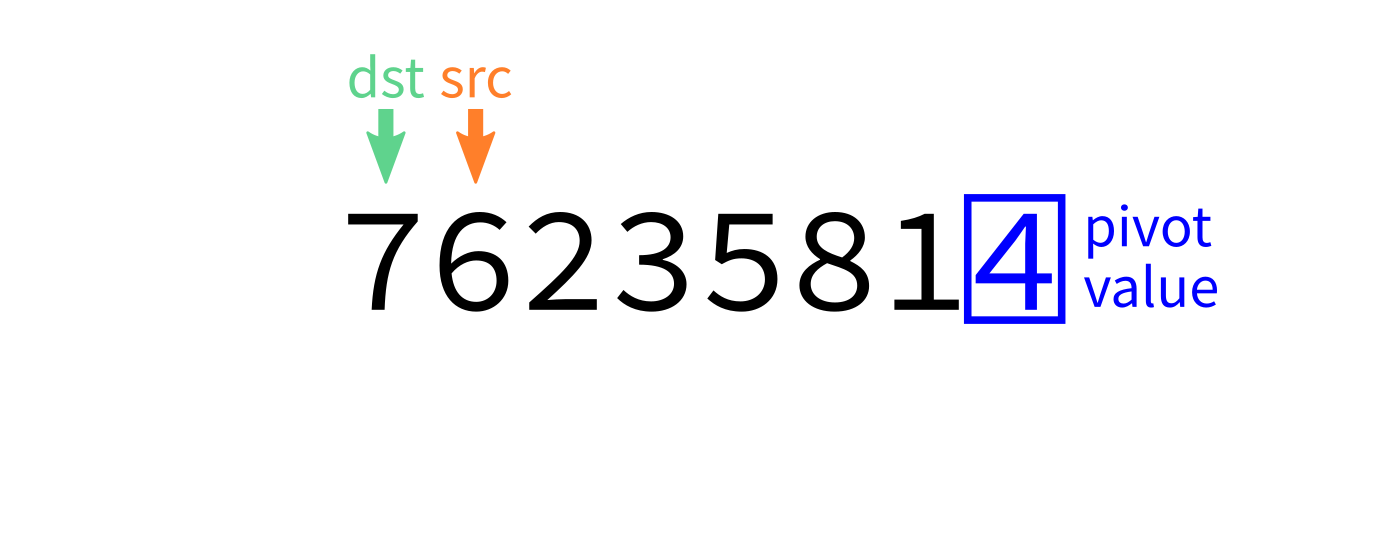
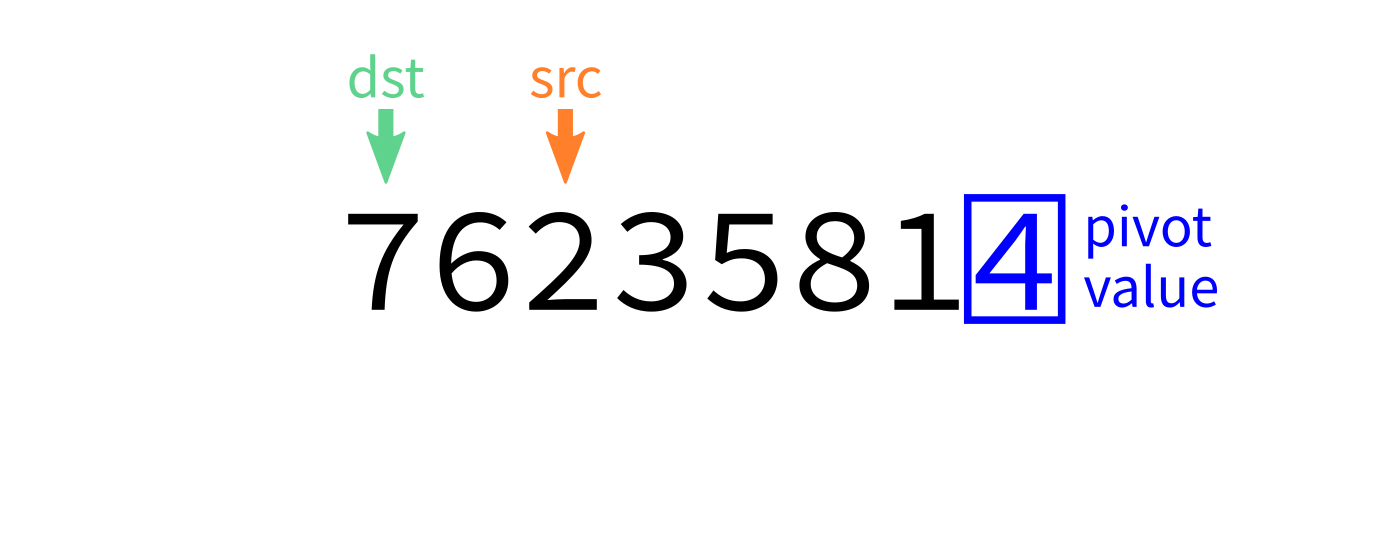
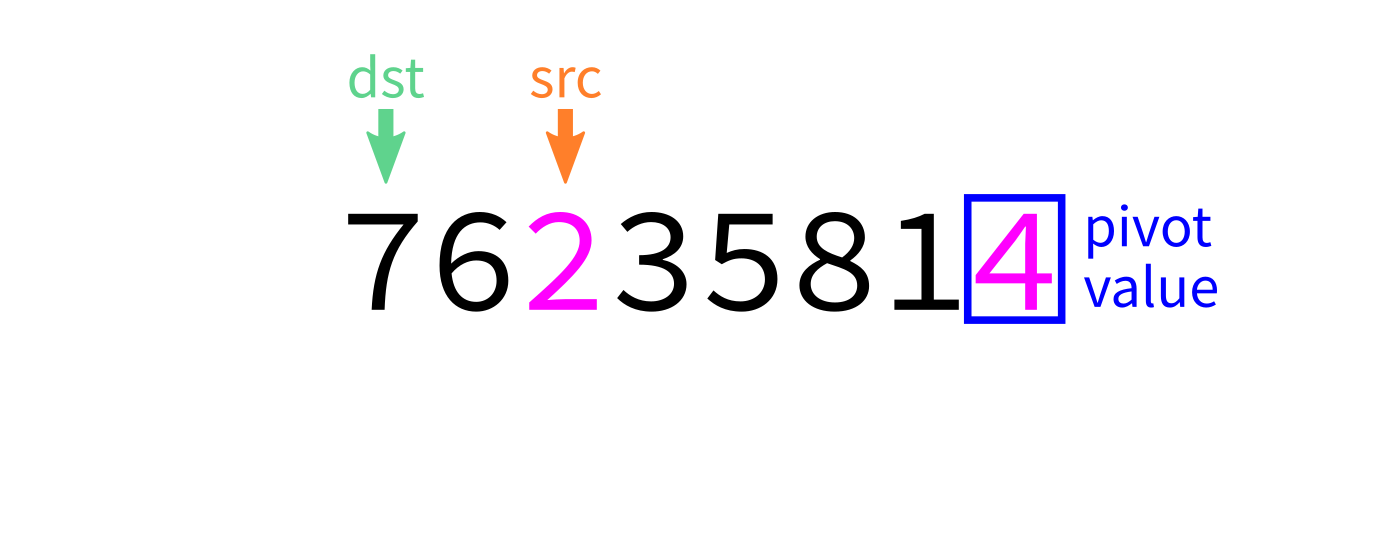

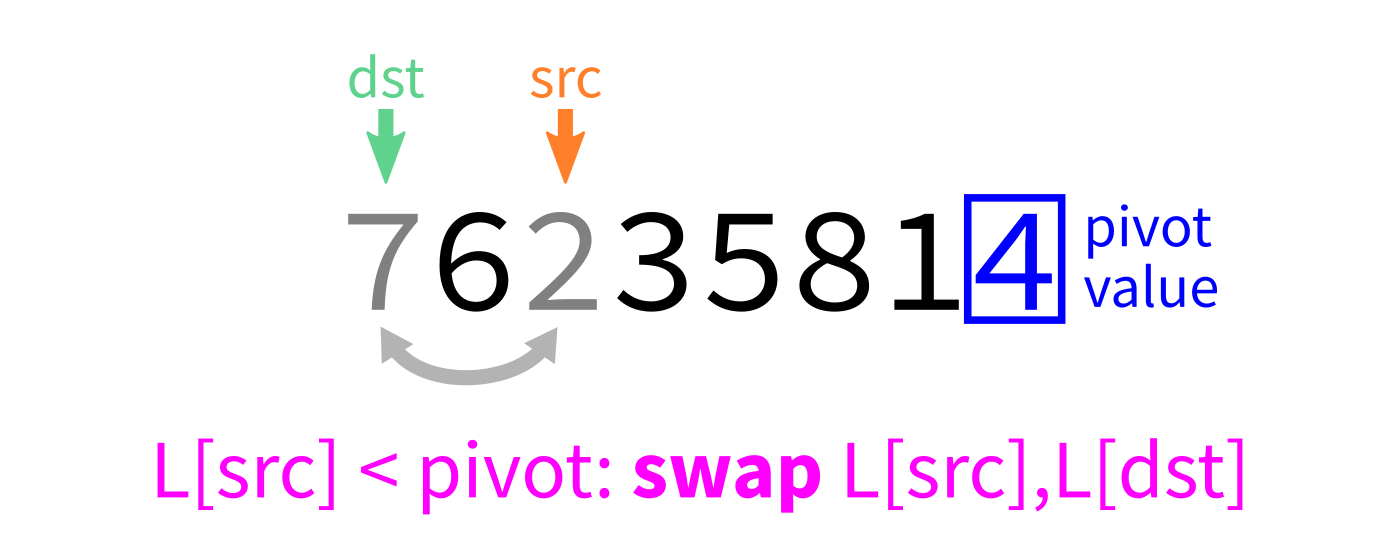







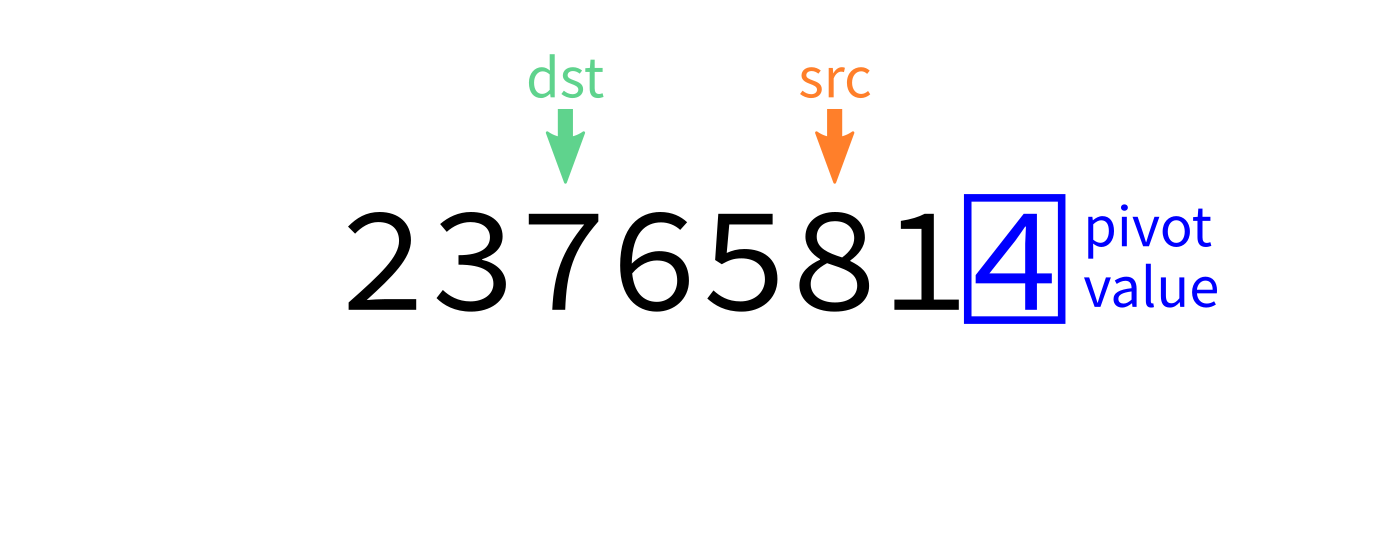
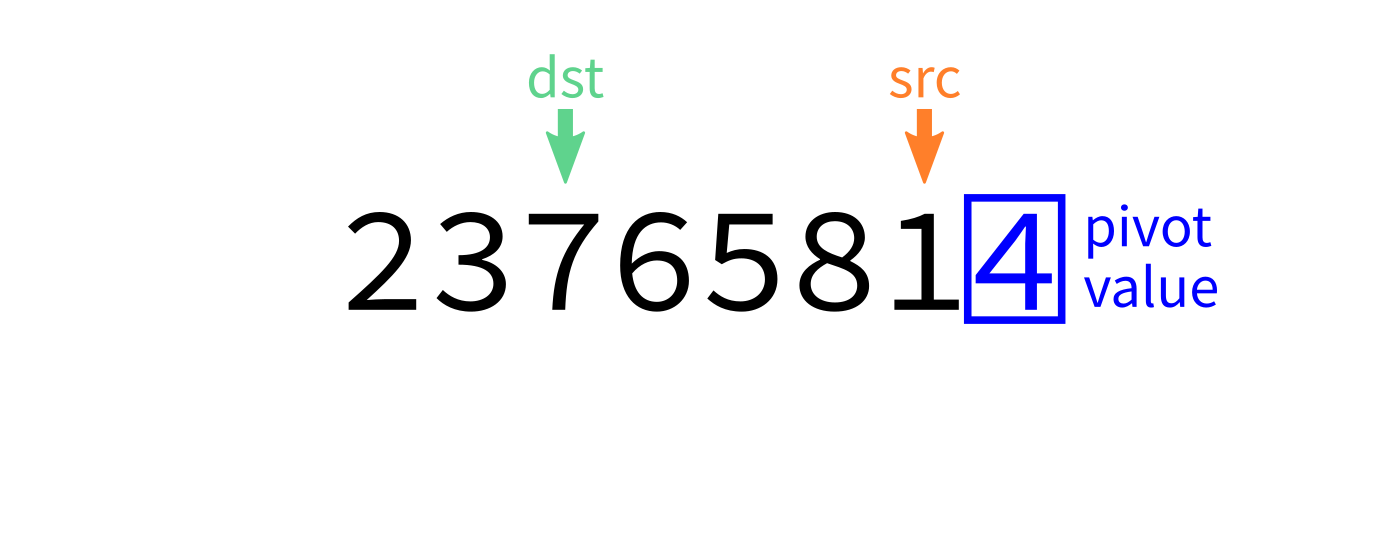

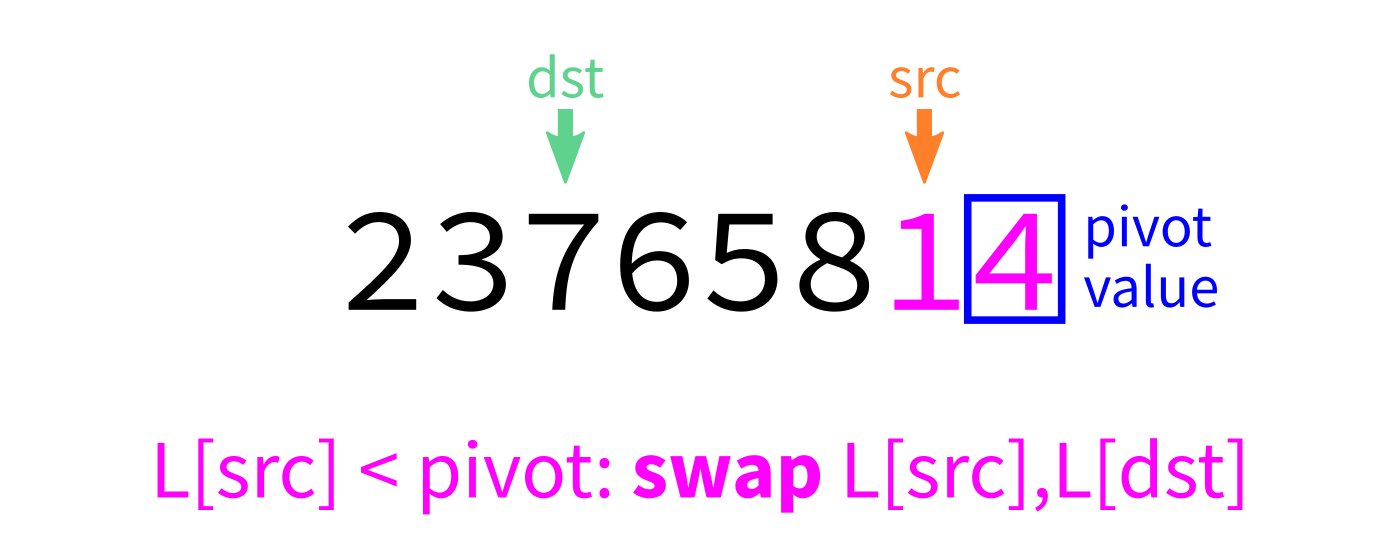
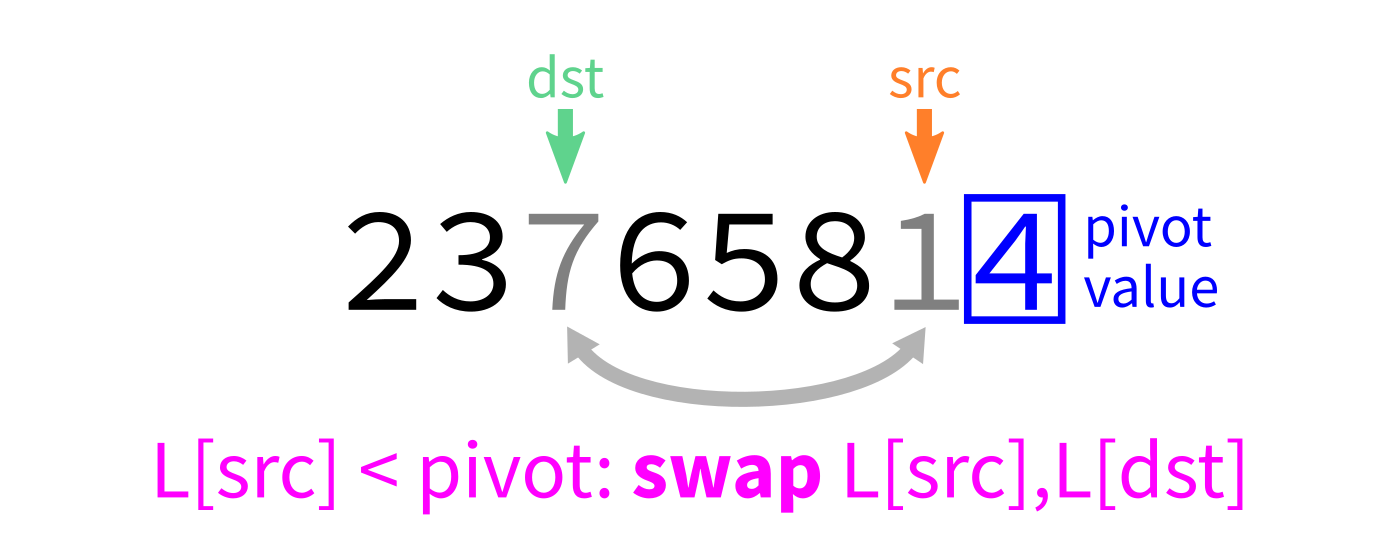
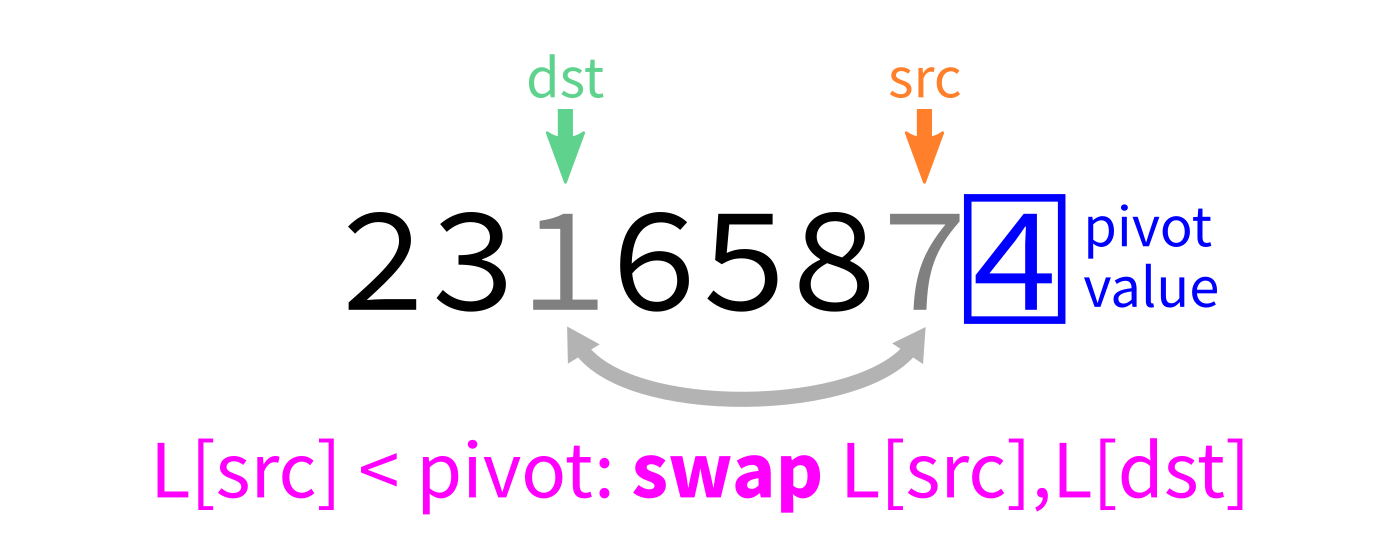
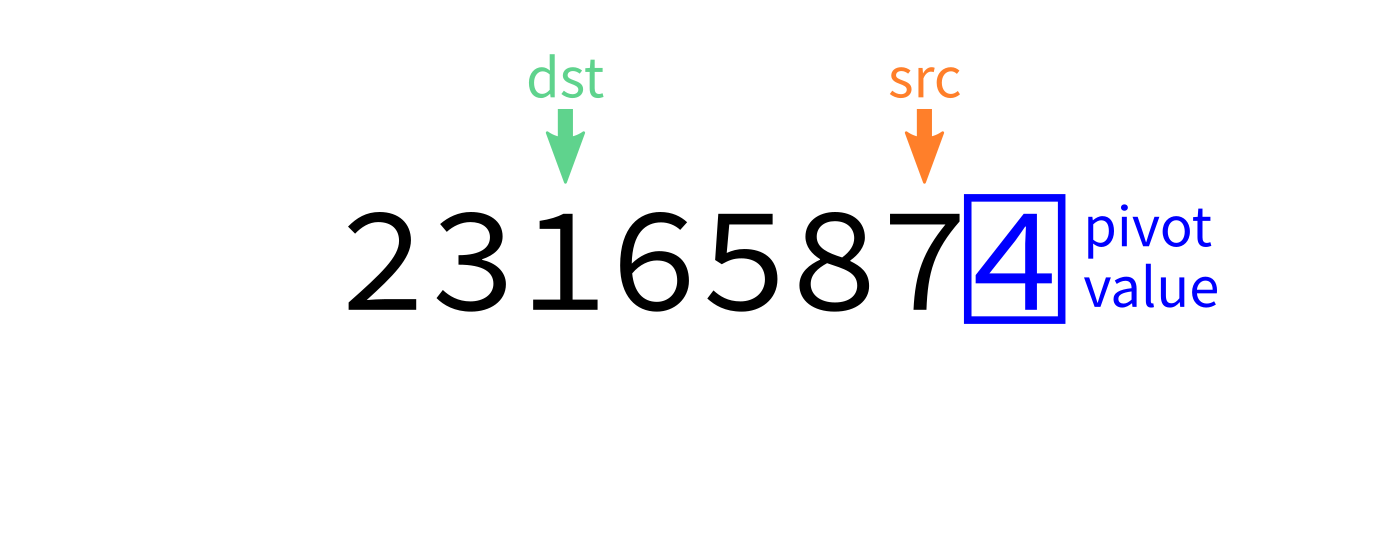
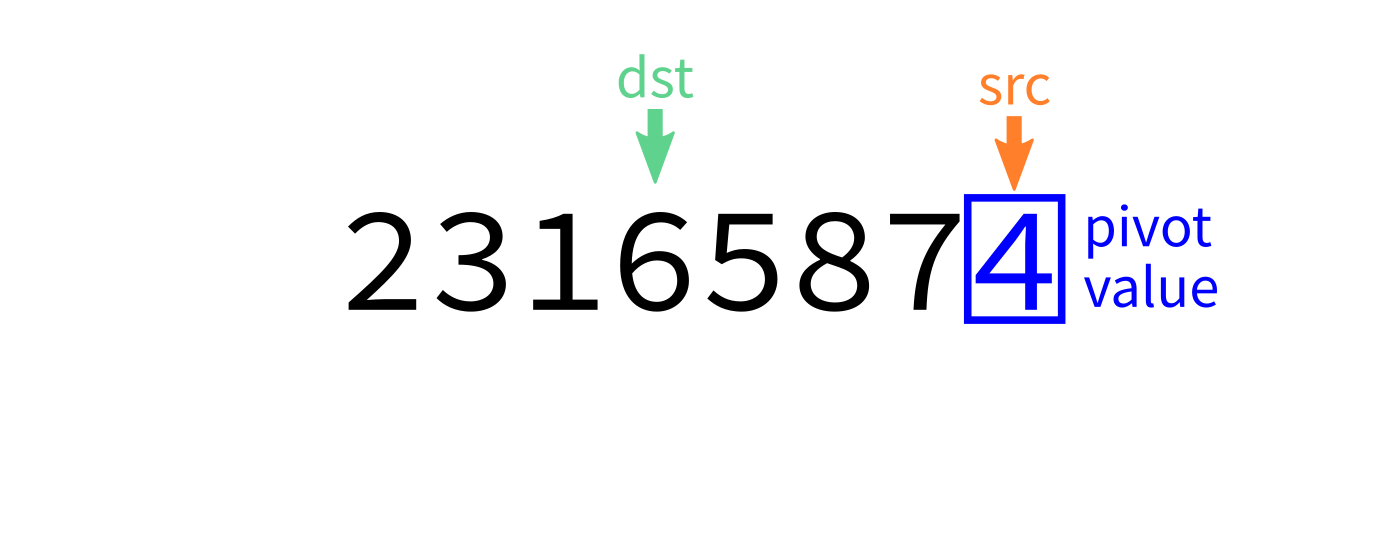
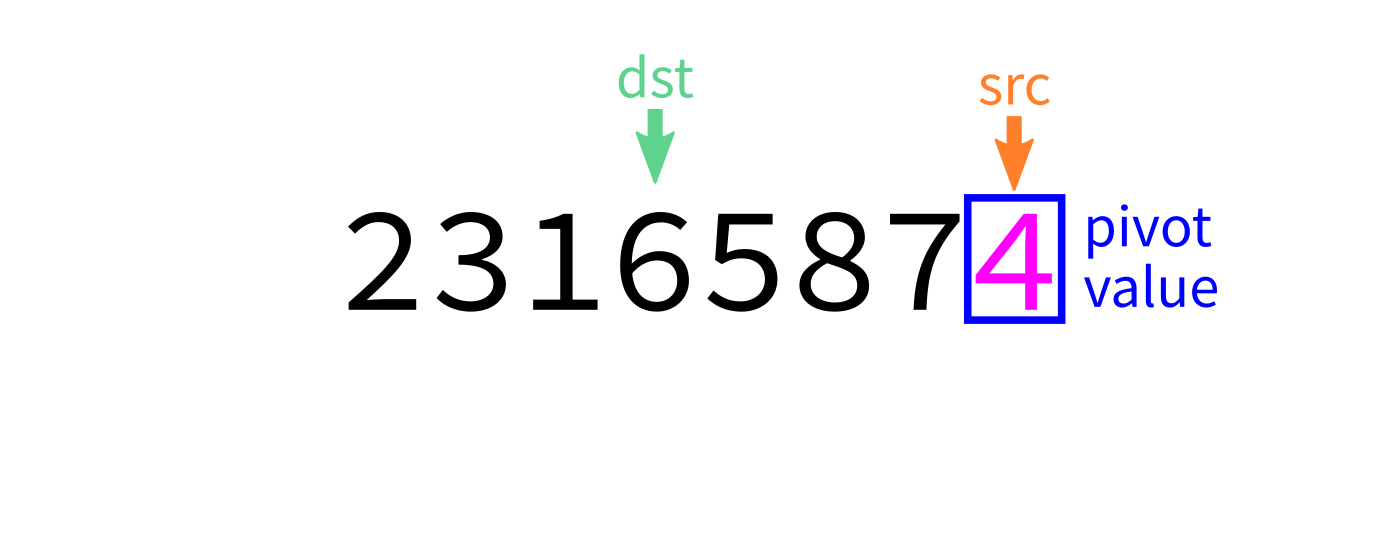


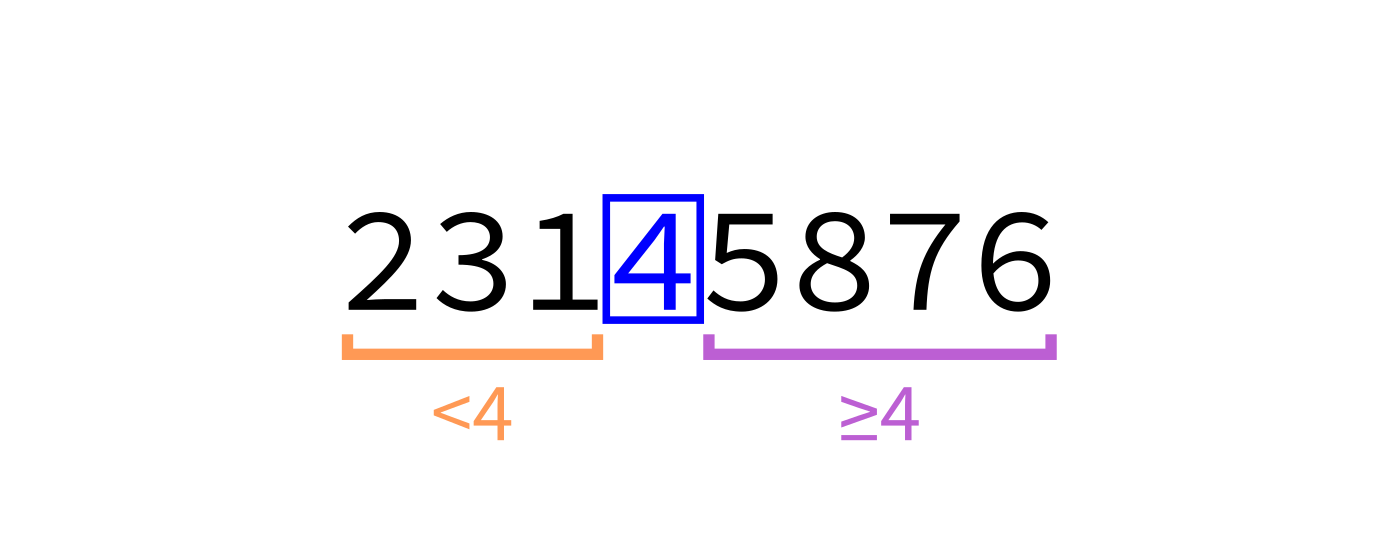
After partition
The two chunks of the list on either side of the pivot may not be sorted.
But we could bring each of them closer to being sorted by partitioning them...
Quicksort summary
Starting with an unsorted list:
- If the list has 0 or 1 elements, return immediately.
- Otherwise, partition the list.
- Quicksort the part of the list before the pivot.
- Quicksort the part of the list after the pivot.
It's divide and conquer, but with no merge step. The hard work is instead in partitioning.
Quicksort visualization
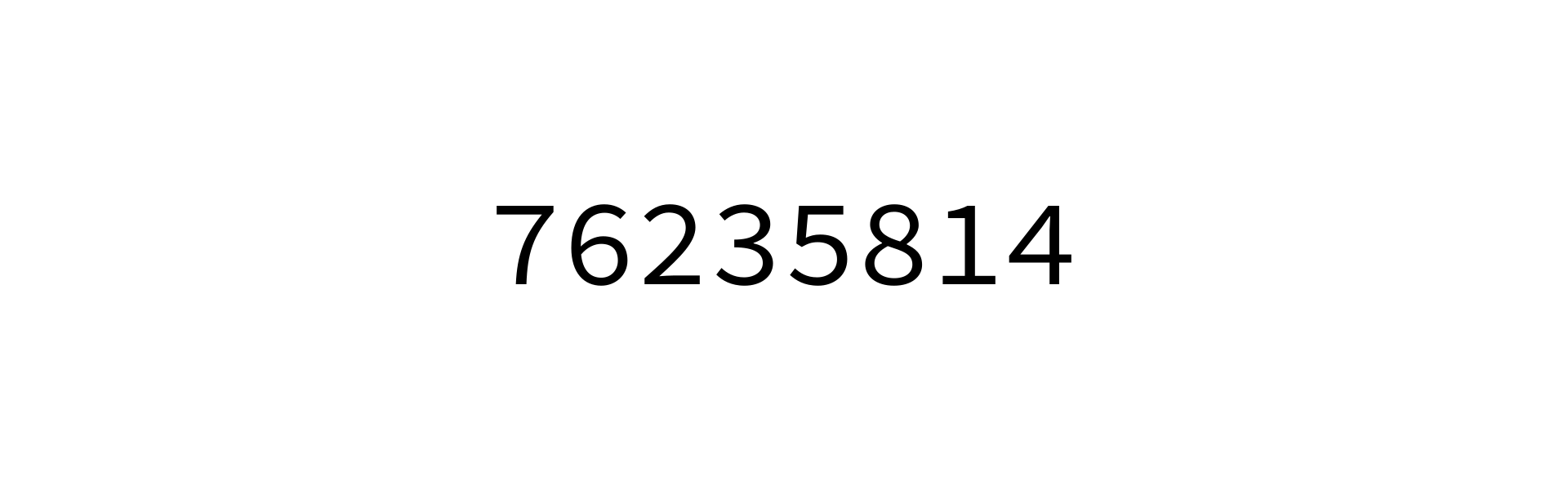





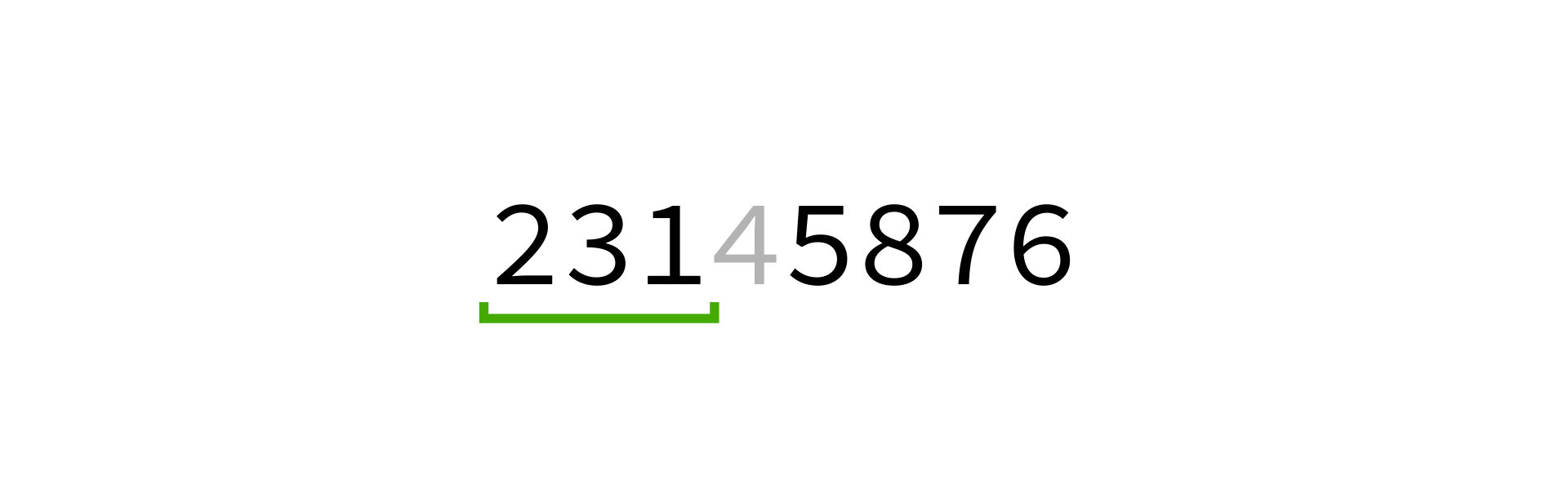
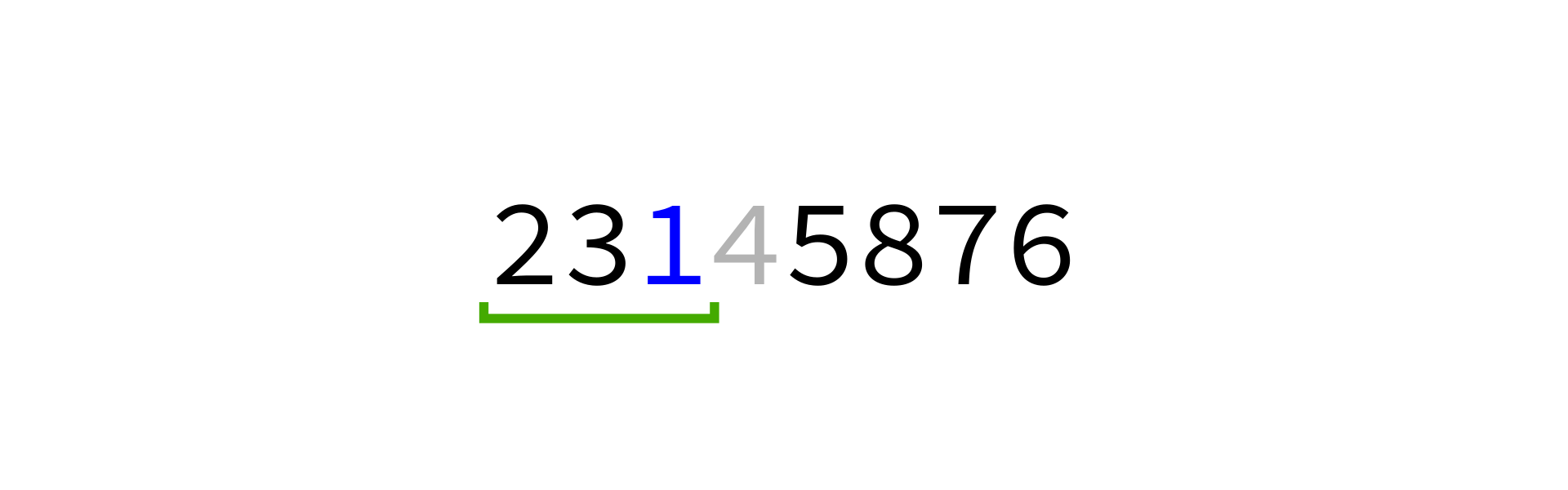
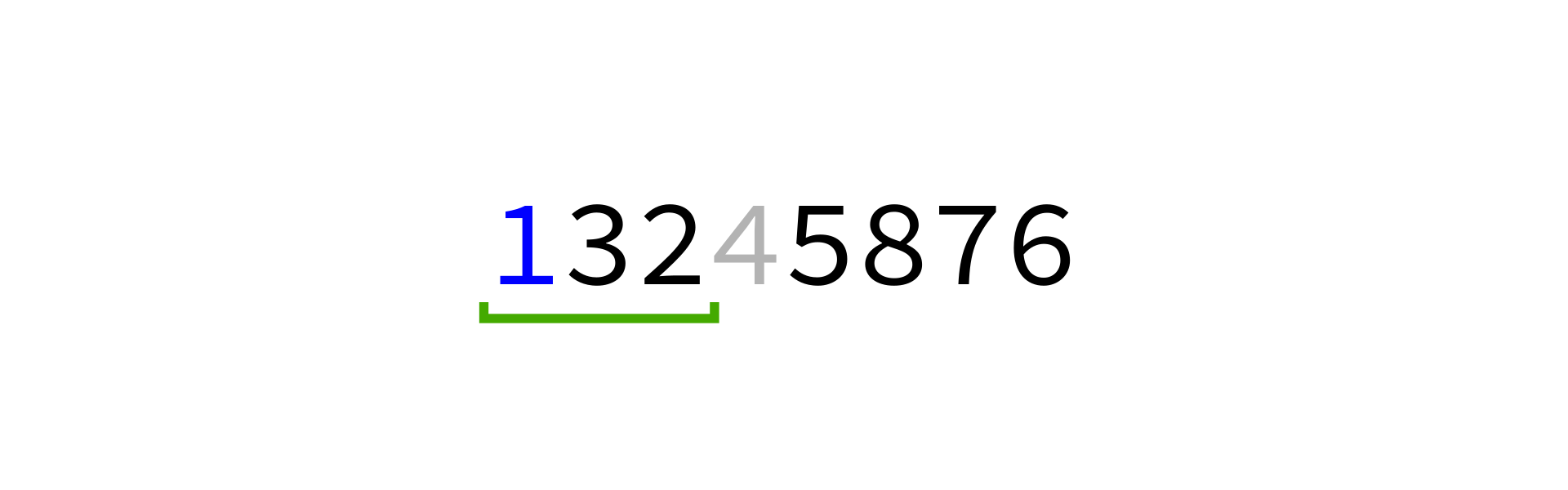
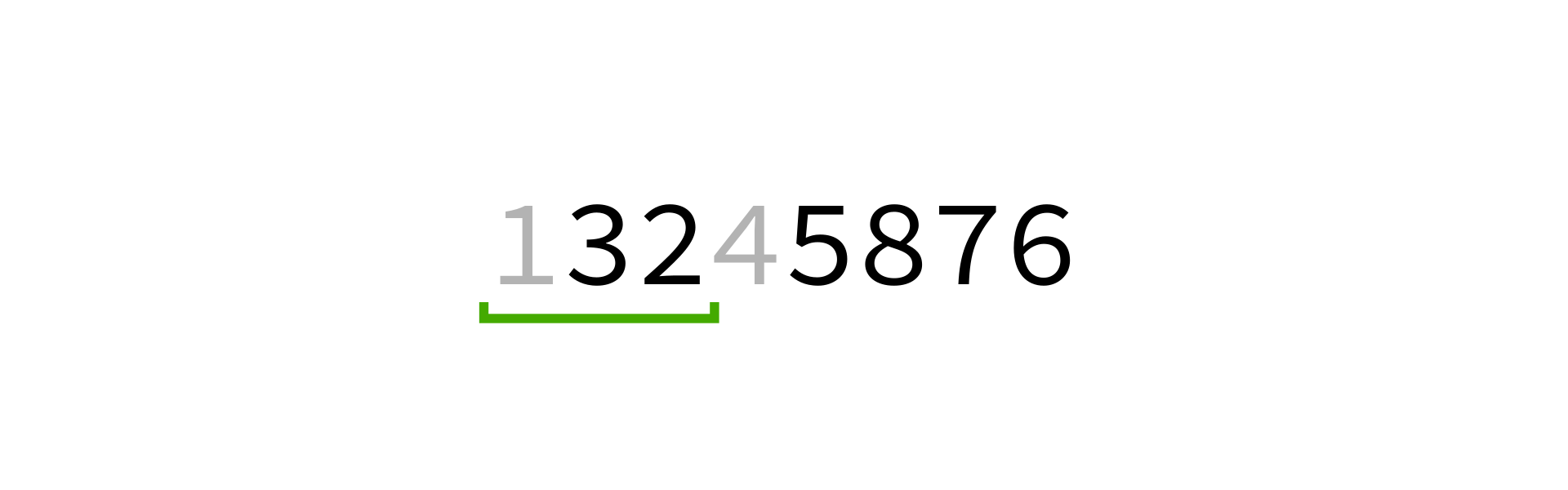
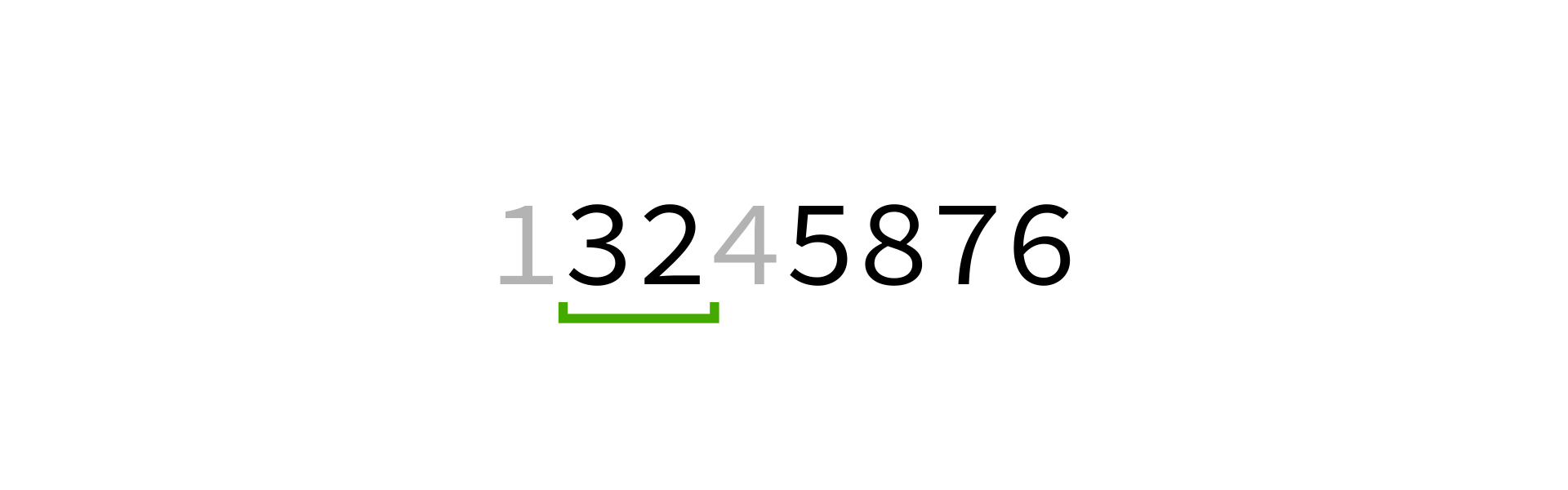
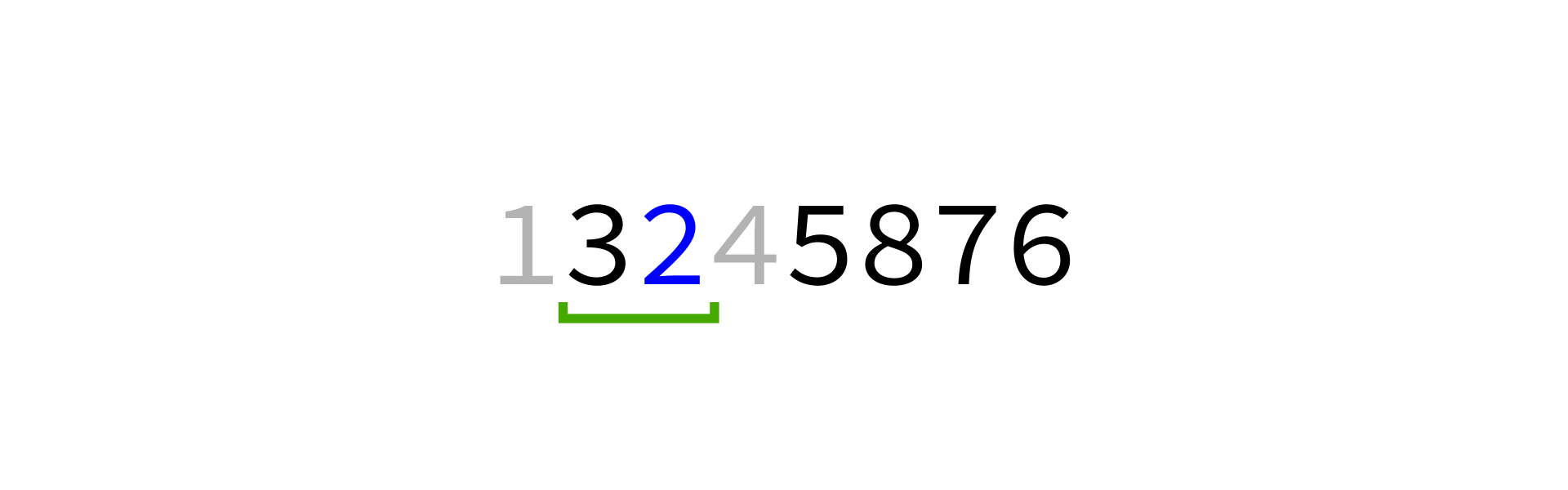
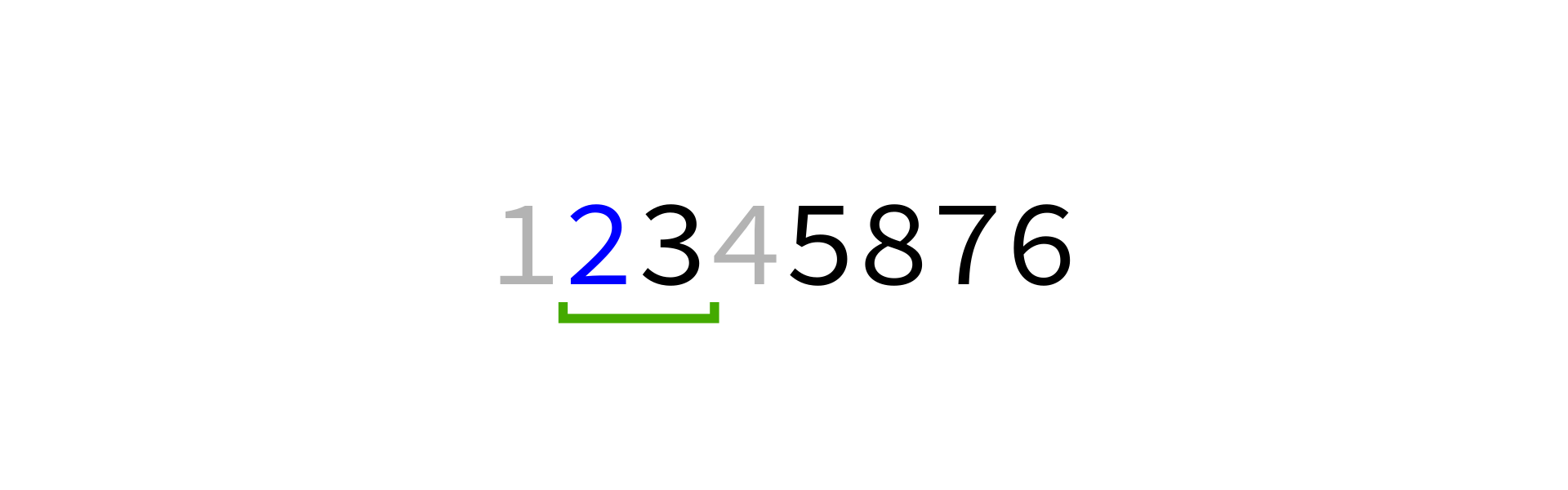
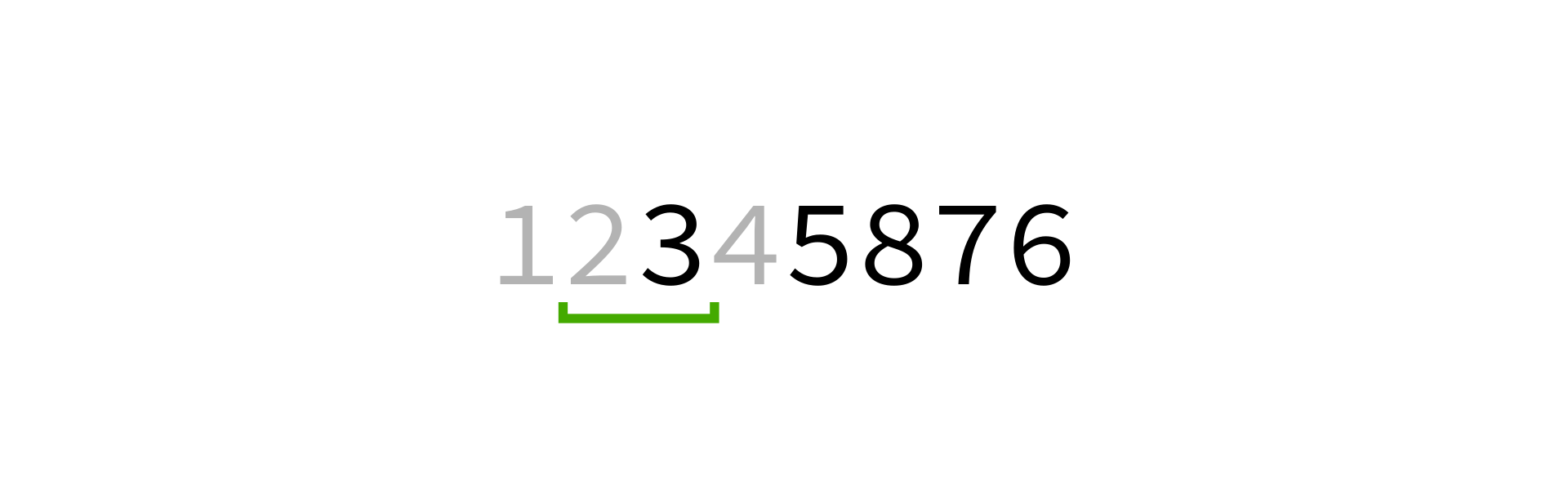
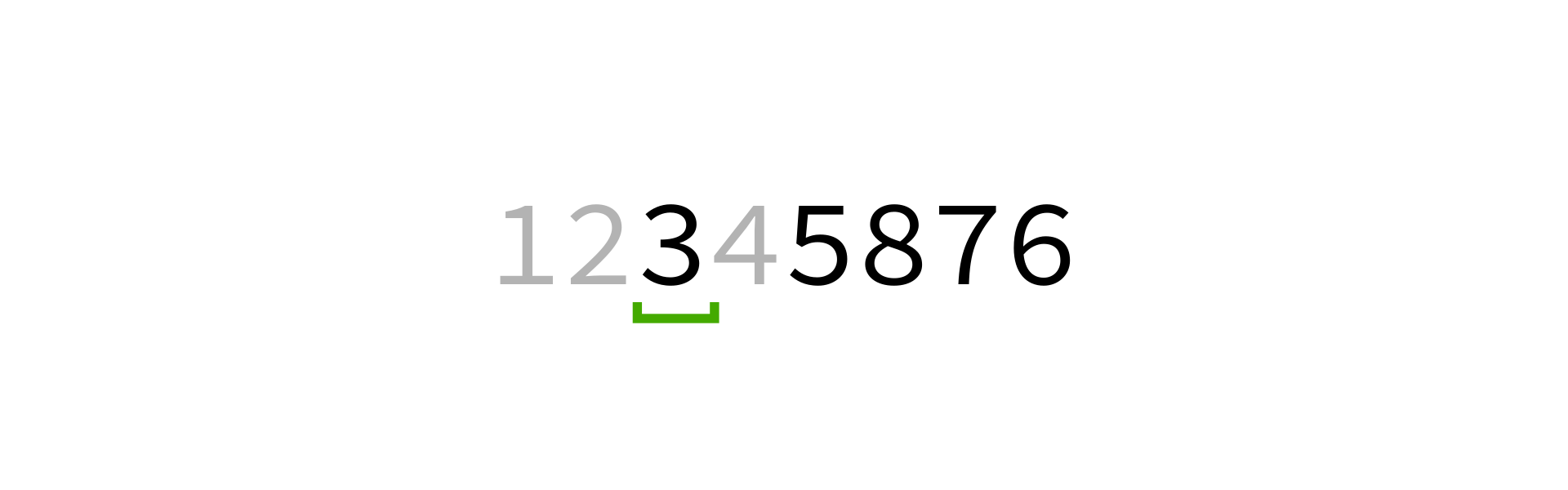
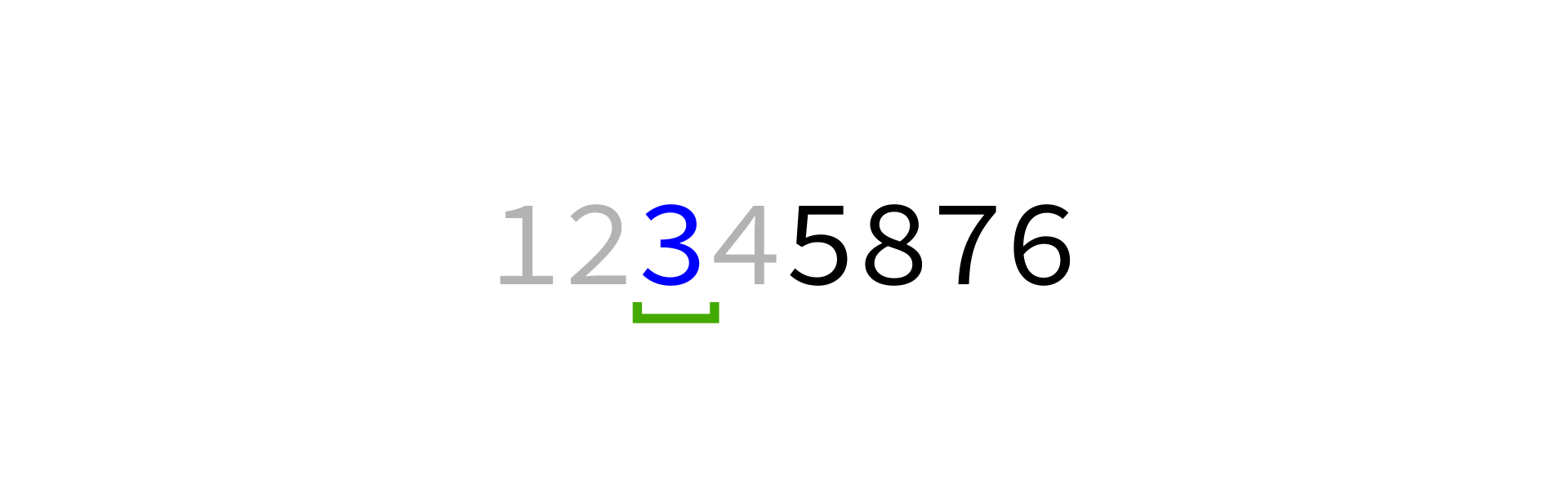


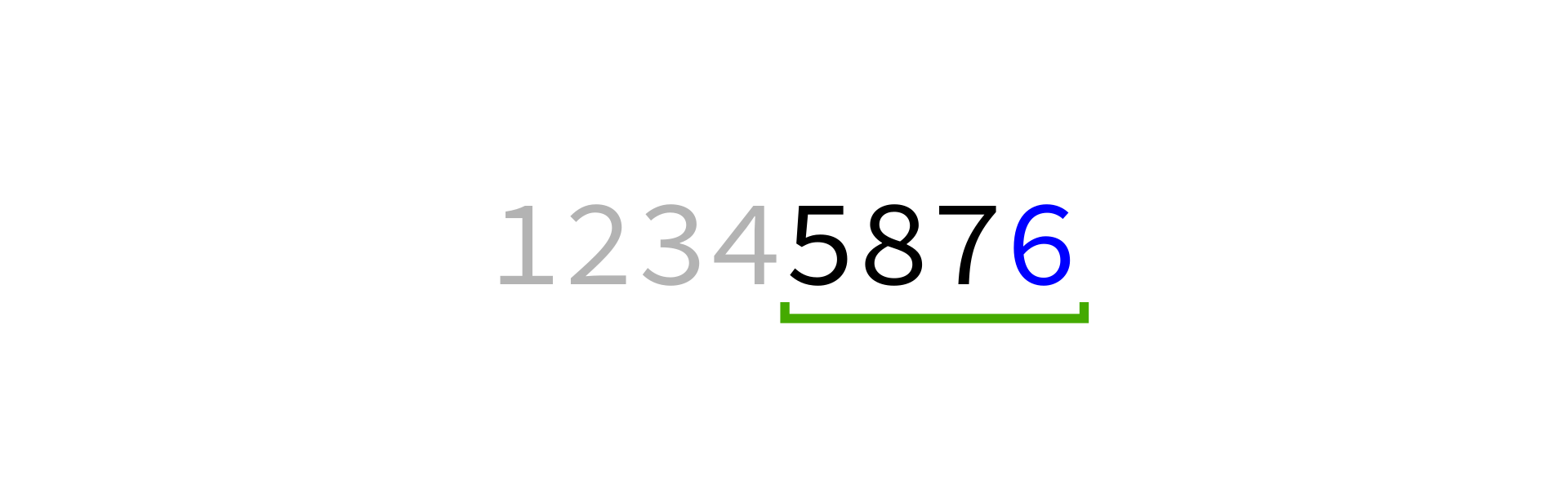


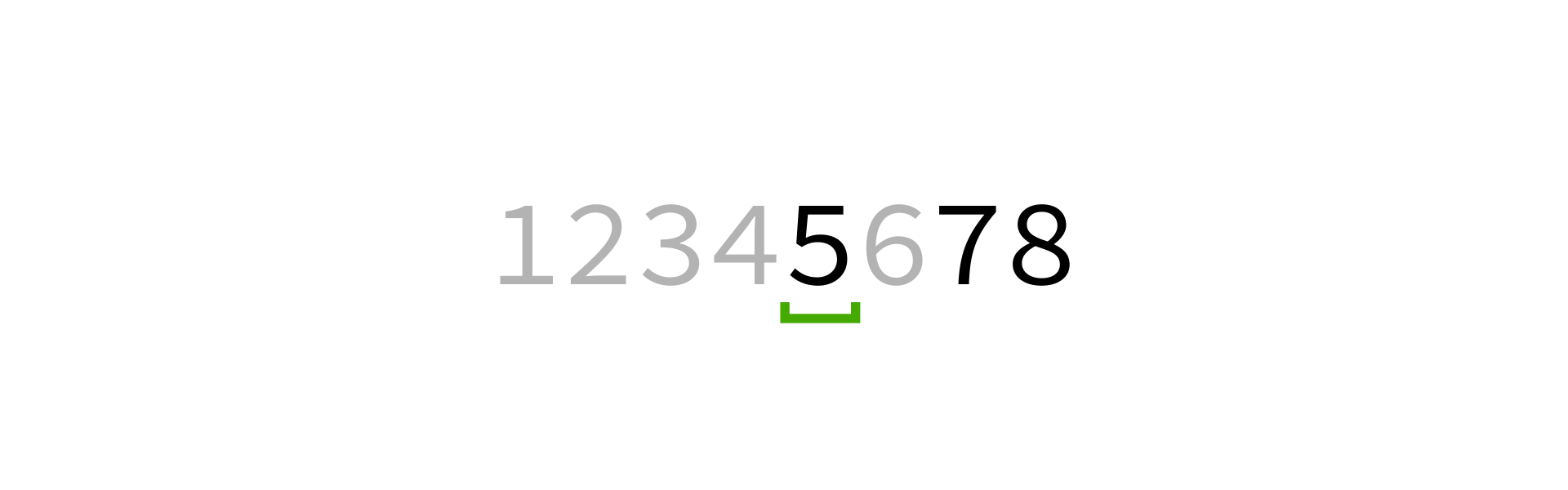





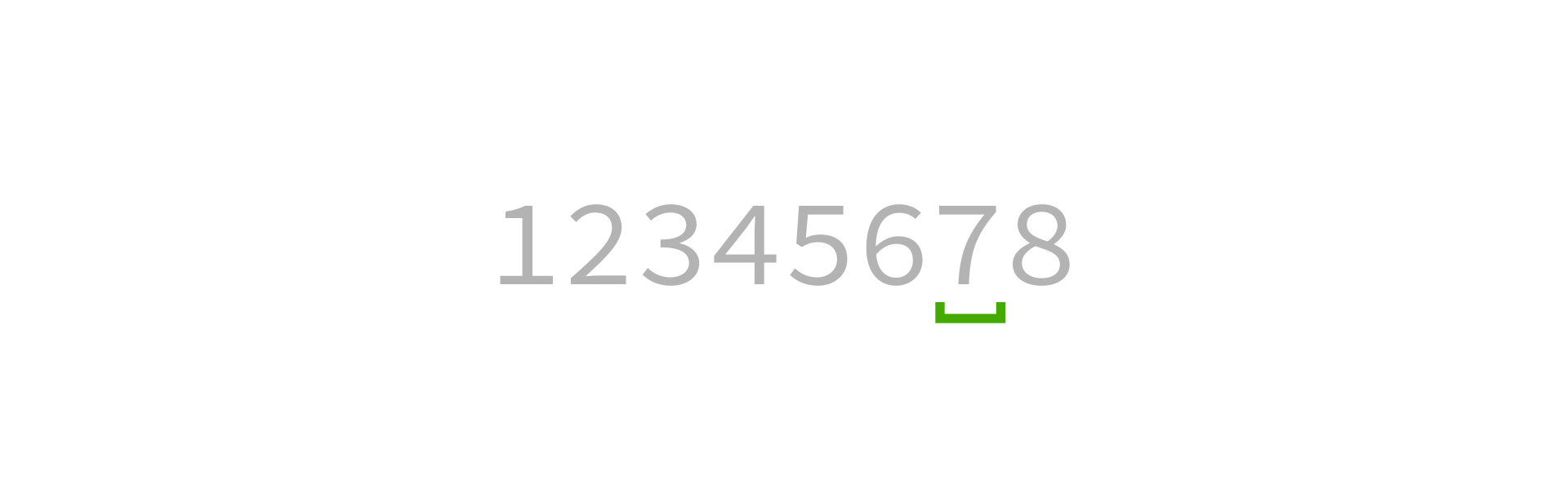


Coding time
Let's implement quicksort in Python.
quicksort:
Input: list L and indices start and end.
Goal: reorder elements of L so that L[start:end] is
sorted.
- If
(end-start)is less than or equal to 1, return immediately. - Otherwise, call
partition(L)to partition the list, lettingmbe the final location of the pivot. - Call
quicksort(L,start,m)andquicksort(L,m+1,end)to sort the parts of the list on either side of the pivot.
partition:
Input: list L and indices start and end.
Goal: Take L[end-1] as a pivot, and reorder elements of L
to partition L[start:end] accordingly.
- Let
pivot=L[end-1]. - Initialize integer index
dst=start. - For each integer
srcfromstarttoend-1: - If
L[src] < pivot, swapL[src]andL[dst]and incrementdst. - Swap
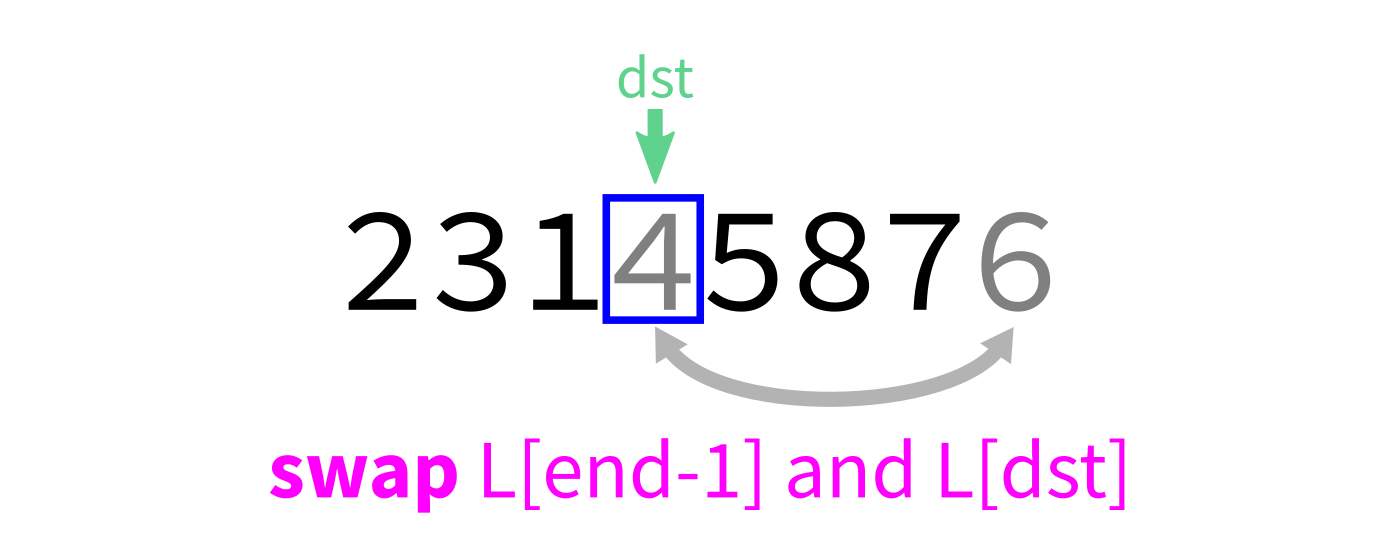
L[end-1]andL[dst]to put the pivot in its proper place. - Return
dst.
Why discuss algorithms?
Python lists have built-in .sort() method. Why talk about sorting?
- Study cases of easy-to-explain problems solved in clever ways.
- See patterns of thinking that work in other settings.
Evaluating sorts
Last time we discussed and implemented mergesort, developed by von Neumann (1945) and Goldstine (1947).
Today we discussed quicksort, first described by Hoare (1959) and the simpler partitioning scheme introduced by Lomuto.
But are these actually good ways to sort a list?
Efficiency
Theorem: If you measure the time cost of mergesort in any of these terms
- Number of comparisons made
- Number of assignments (e.g.
L[i] = xcounts as 1) - Number of Python statements executed
then the cost to sort a list of length $n$ is less than $C n \log(n)$, for some constant $C$ that only depends on which expense measure you chose.
Asymptotically optimal
$C n \log(n)$ is pretty efficient for an operation that needs to look at all $n$ elements. It's not linear in $n$, but it only grows a little faster than linear functions.
Furthermore, $C n \log(n)$ is the best possible time for comparison sort of $n$ elements (though different methods might have better $C$).
Quicksort
Is quicksort similarly efficient?
References
- Recursion references from Lecture 9.
- Sorting visualizations:
- 2D visualization through color sorting by Linus Lee
- Animated bar graph visualization of many sorting algorithms by Alex Macy
- Slanted line animated visualizations of mergesort and quicksort by Mike Bostock
Revision history
- 2023-02-15 Finalization of the 2023 lecture this was based on
- 2024-02-07 Initial publication