Lecture 14
Comparison sorts
MCS 275 Spring 2024
Emily Dumas
Lecture 14: Comparison sorts
Reminders and announcements:
- Homework 5 posted.
- Project 1 due at 11:59pm tonight.
- Project 2 coming Monday, is due on Fri Feb 23.
- Starting new topic (trees) next week.
Evaluating sorts
On Monday we discussed and implemented mergesort, developed by von Neumann (1945) and Goldstine (1947).
On Wednesday we discussed quicksort, first described by Hoare (1959), though we used a simpler partition implementation developed by Lomuto.
But are these actually good ways to sort a list?
Mergesort recursion tree
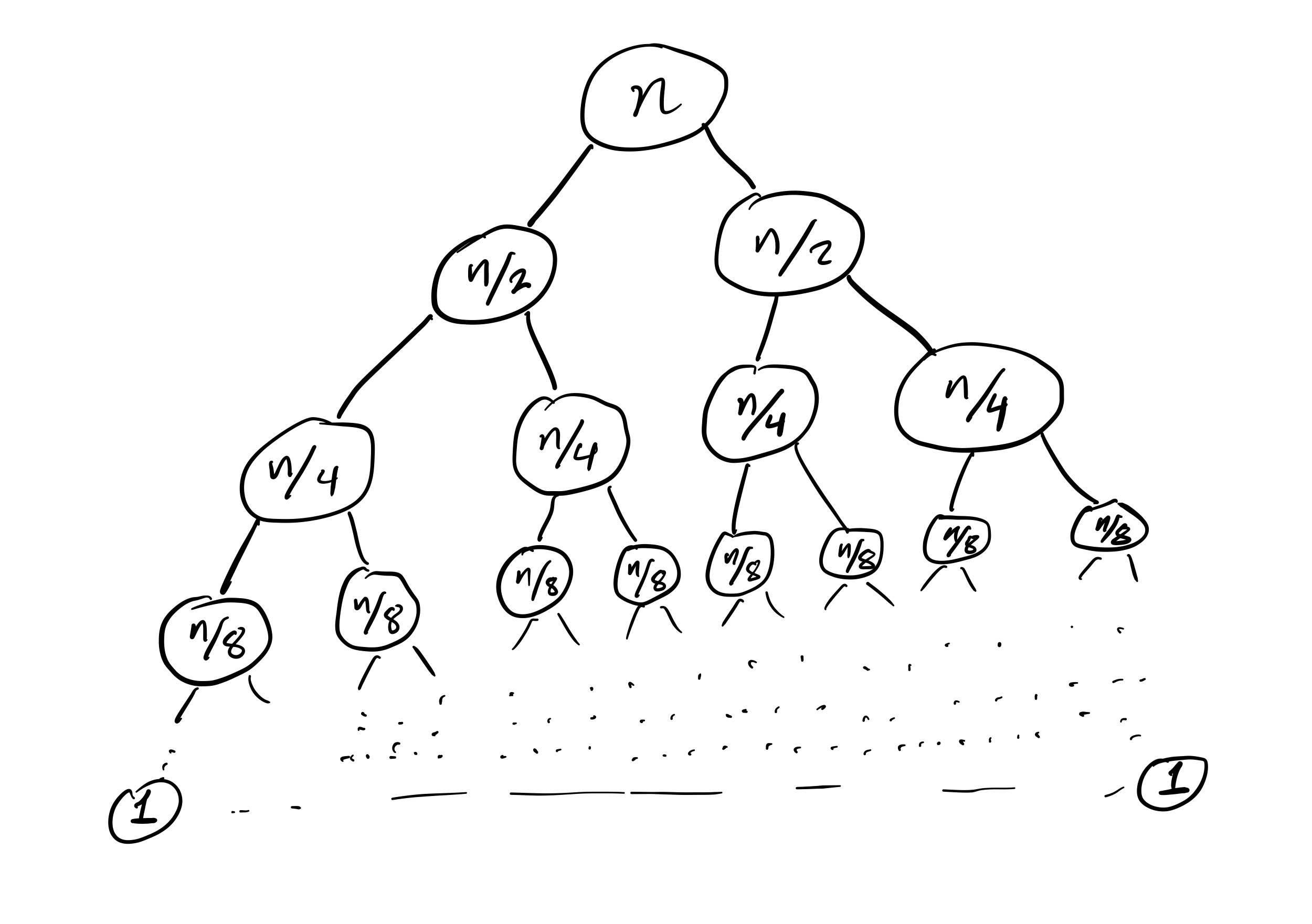
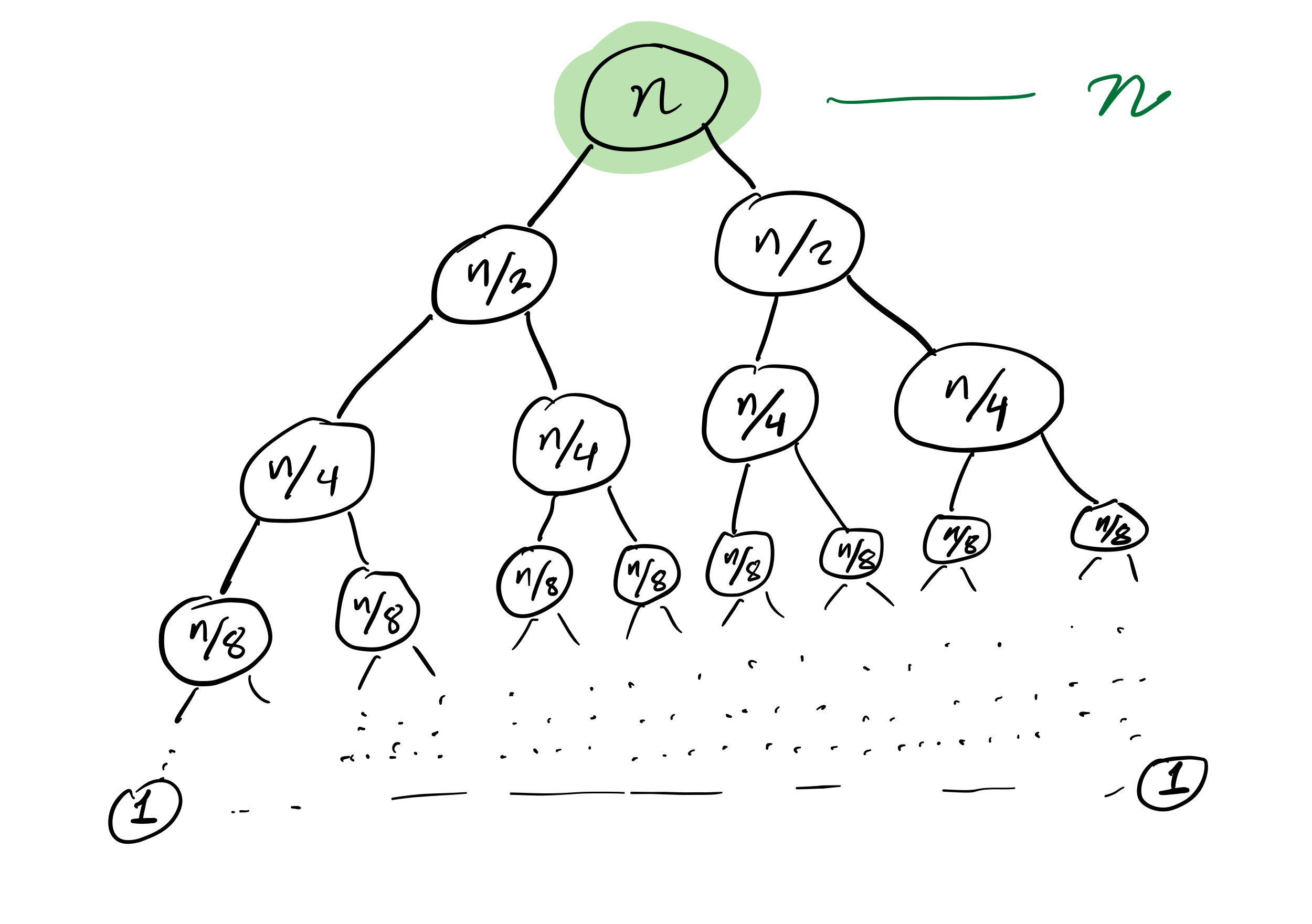
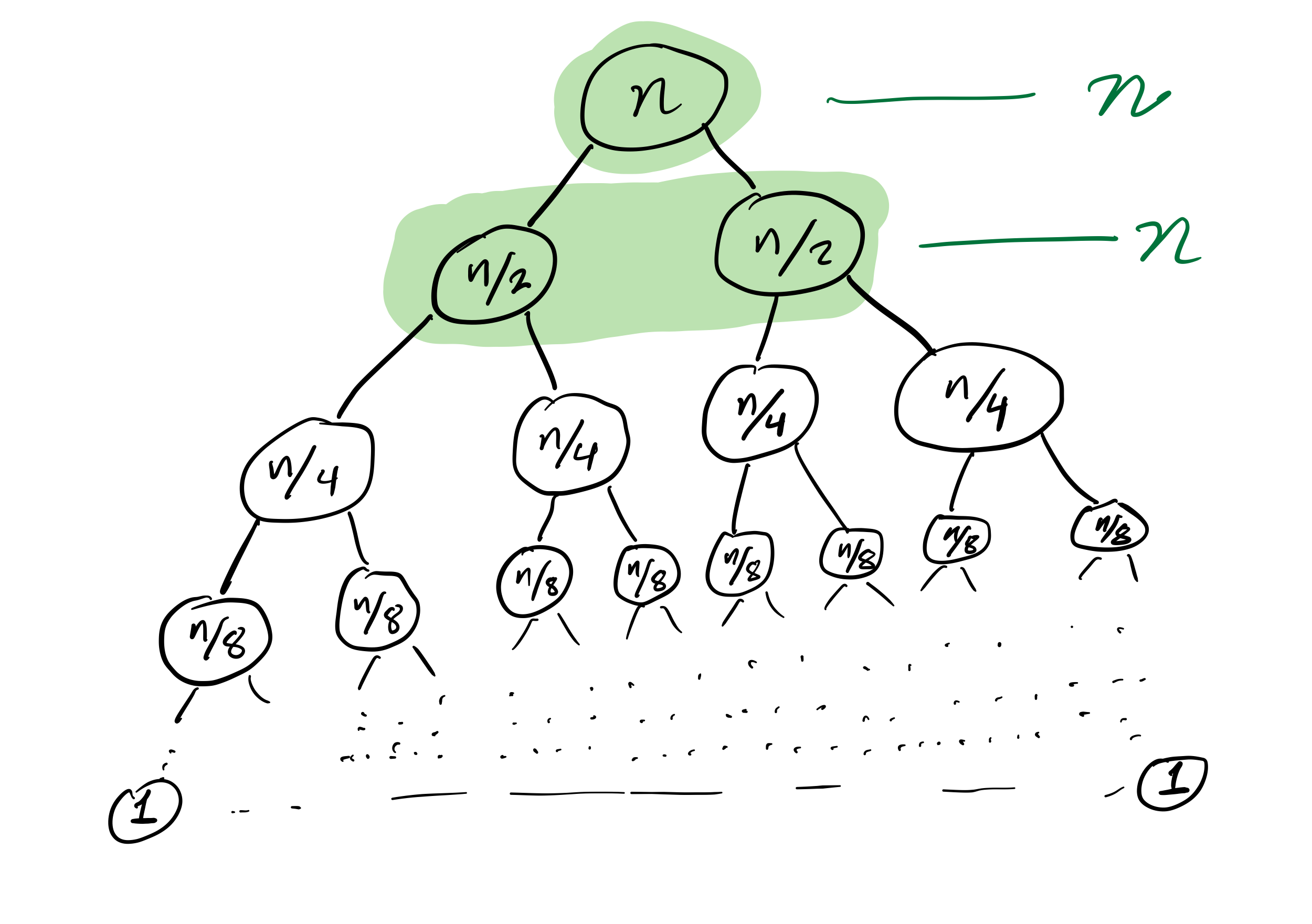
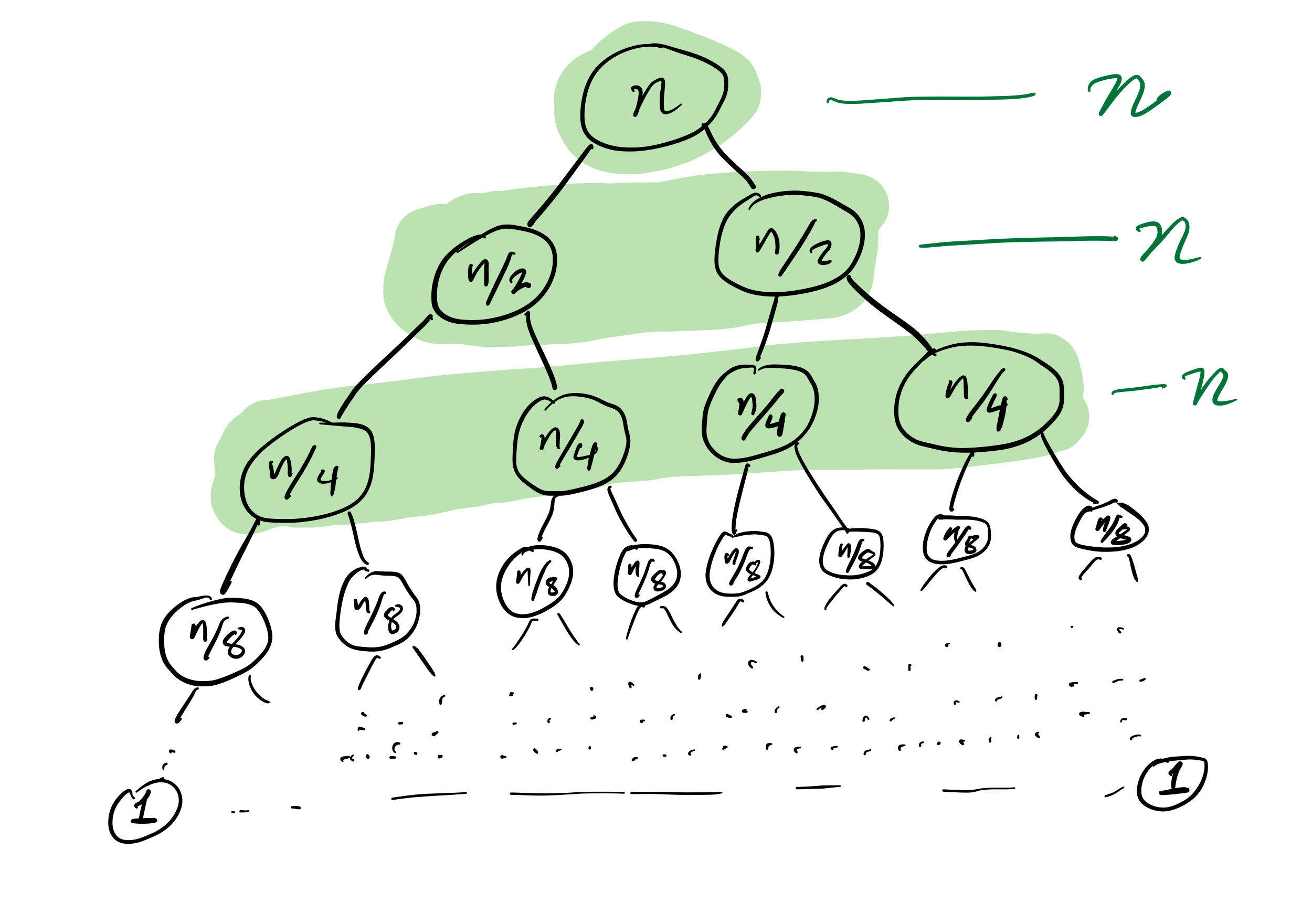
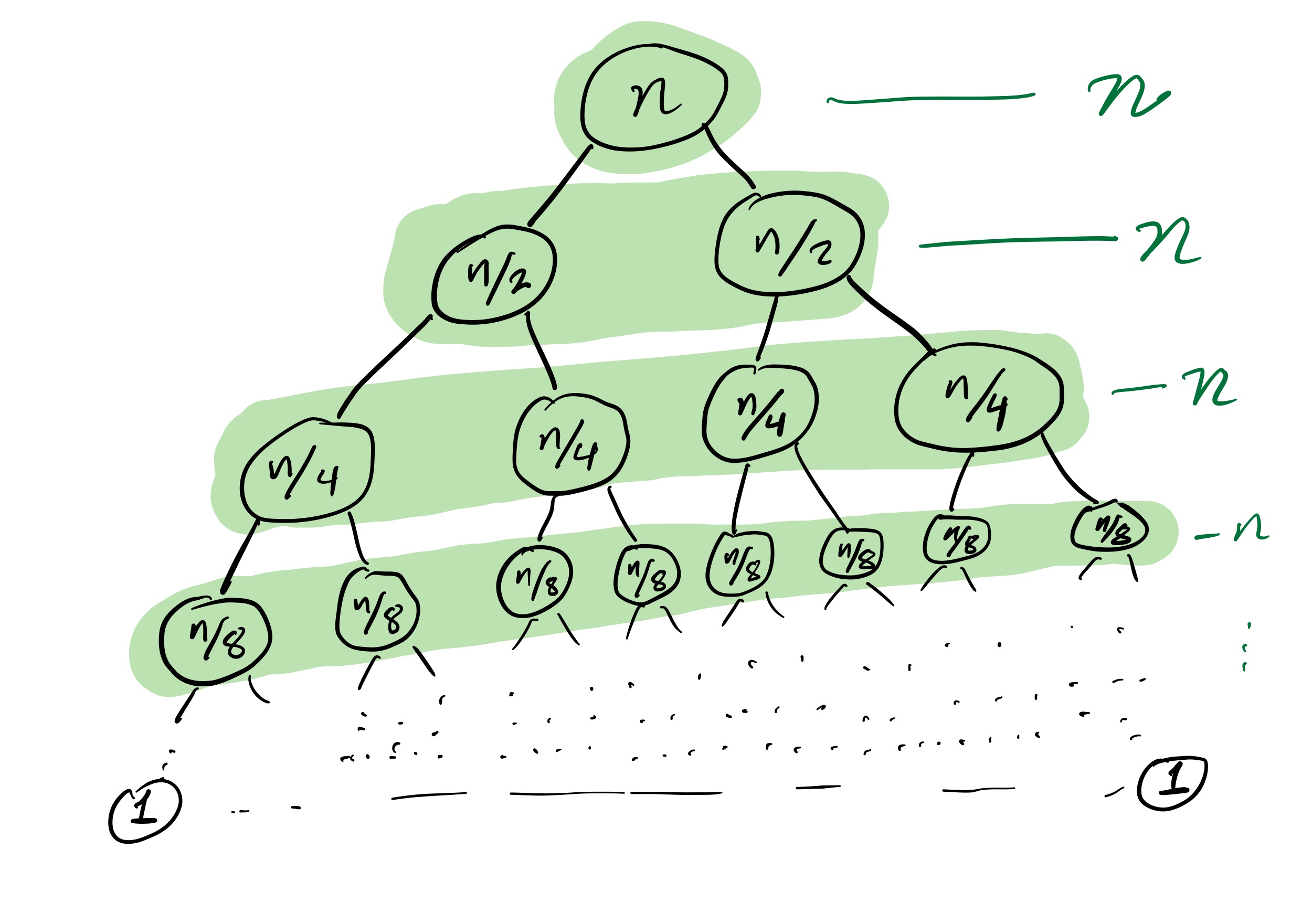
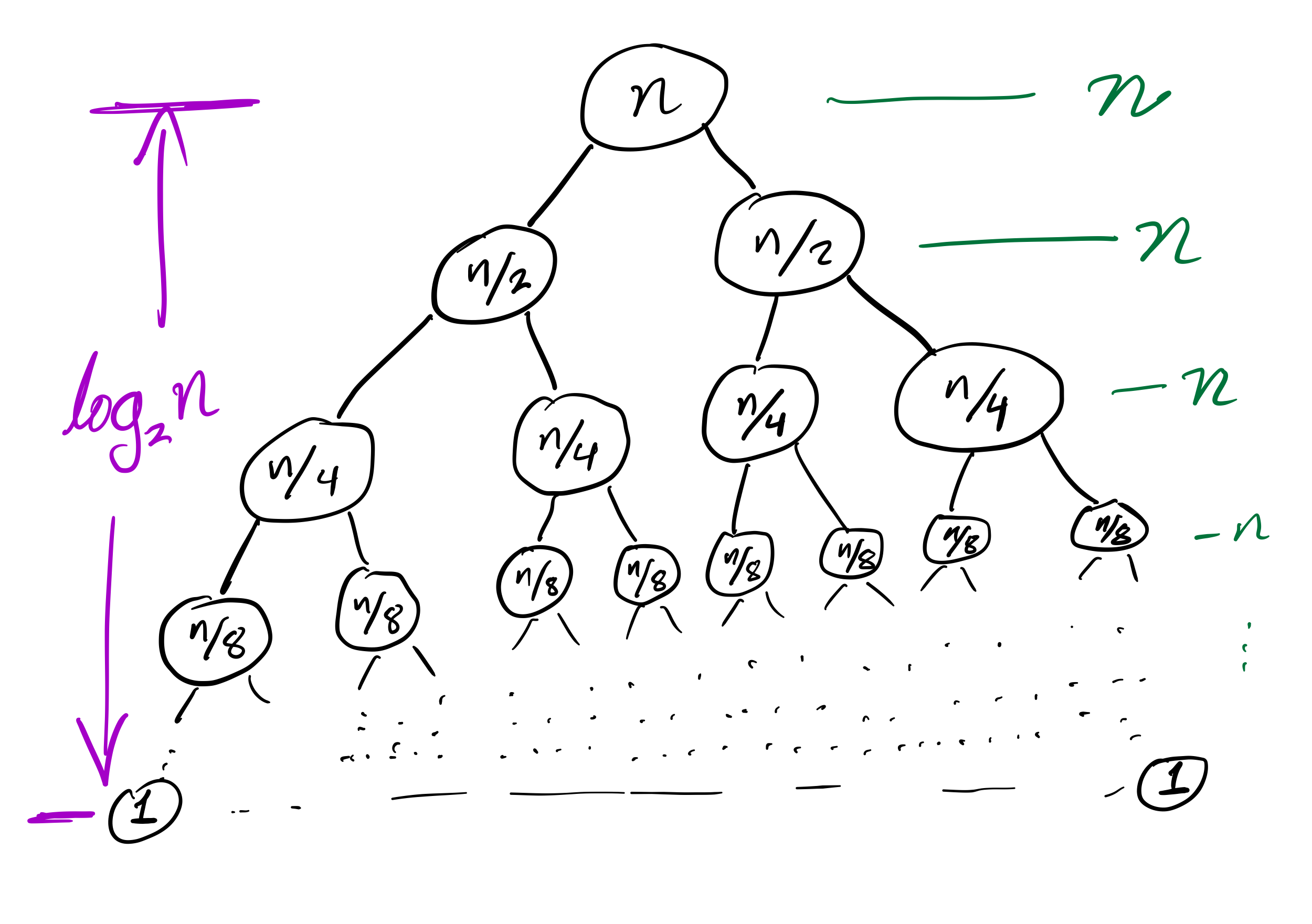
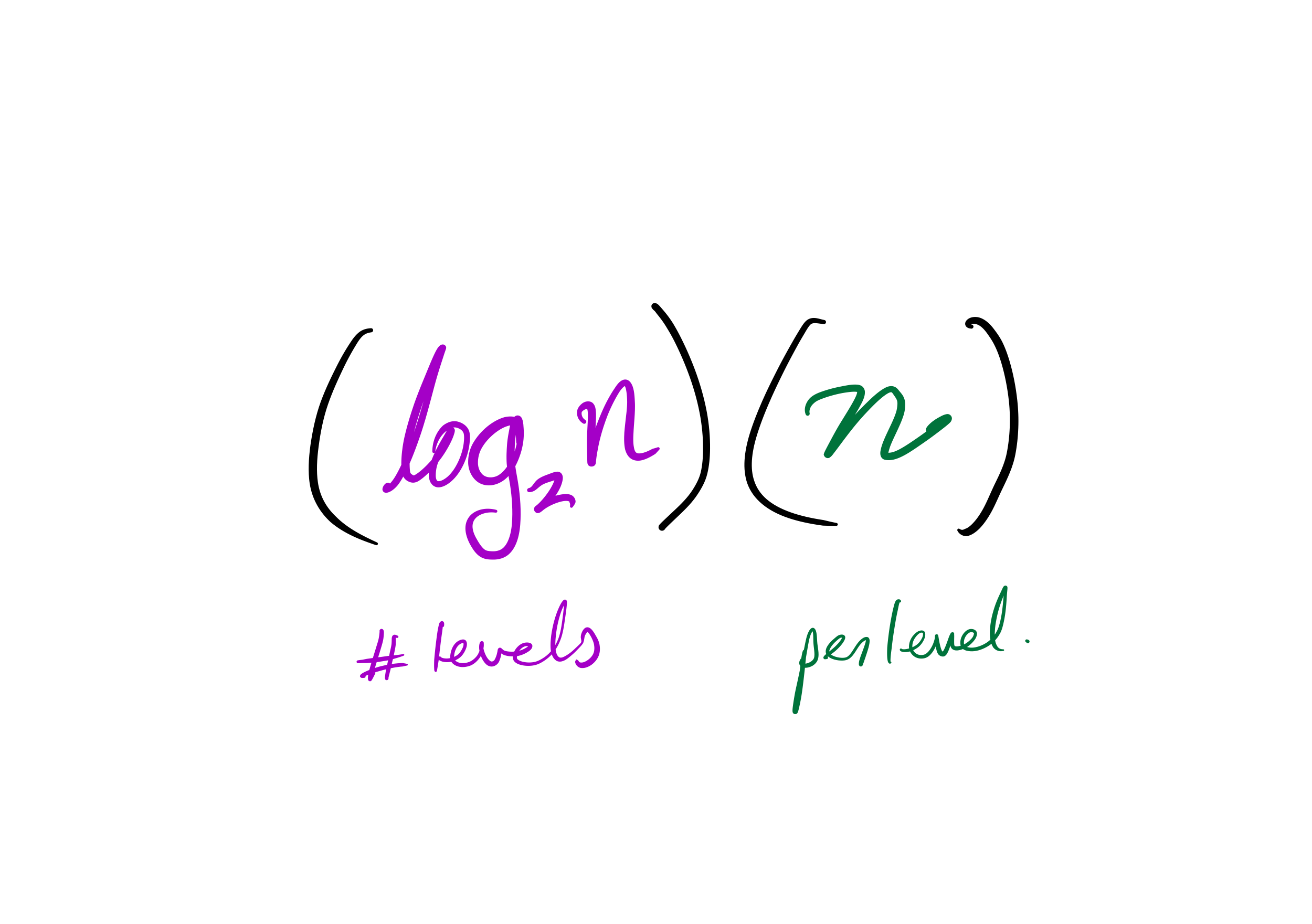


Efficiency
Theorem: If you measure the time cost of mergesort in any of these terms
- Number of comparisons made
- Number of assignments (e.g.
L[i] = xcounts as 1) - Number of Python statements executed
then the cost to sort a list of length $n$ is less than $C n \log(n)$, for some constant $C$ that only depends on which expense measure you chose.
But is that good or bad?
Juan says you can make a comparison sort that handles any 3-item list using at most 3 comparisons.
Anna says this is impossible, i.e. sorting 3 things sometimes requires more than 3 comparisons.
Who's right?
Given [a,b,c] you might ask a<b, b<c, a<c.
There are $3!=6$ possible sorted orders for [a,b,c] and they all give different combinations of answers!
Juan is right.
Juan says you can make a comparison sort that handles any 6-item list using at most 8 comparisons.
Anna says this is impossible.
Who's right?
There are $6!=720$ ways to reorder the numbers [1,2,3,4,5,6].
In each case, a different combination of actions is needed to put the list back in order.
But with $8$ comparisons there are only $2^8 = 256$ possible sets of answers.
So based on these comparisons a function could only have $256$ different behaviors, which is too few to handle all 6-item lists.
Anna is right.
Complexity
This leads to...
Theorem: If a comparison sort performs at most $c$ comparisons when given a list of $n$ item, then $$2^c \geq n!$$
Corollary: $C n \log(n)$ is the best possible time for comparison sort of $n$ items (the only thing you can do is try to decrease $C$).
Looking back on quicksort
It ought to be called partitionsort because the algorithm is simply:
- Partition the list
- Quicksort the part before the pivot
- Quicksort the part after the pivot
Other partition strategies
We used the last item of the list as a pivot. Other popular choices:
- The first item,
L[start] - A random item of
L[start:end] - The item
L[(start+end)//2] - An item near the median of
L[start:end](more complicated to find!)
How to choose?
Knowing something about your starting data may guide choice of partition strategy (or even the choice to use something other than quicksort).
Almost-sorted data is a common special case where first or last pivots are bad.
Efficiency
Theorem: If you measure the time cost of quicksort in any of these terms
- Number of comparisons made
- Number of swaps or assignments
- Number of Python statements executed
then the cost to sort a list of length $n$ is less than $C n^2$, for some constant $C$.
But if you average over all possible orders of the input data, the result is less than $C n \log(n)$.
Quicksort recursion tree
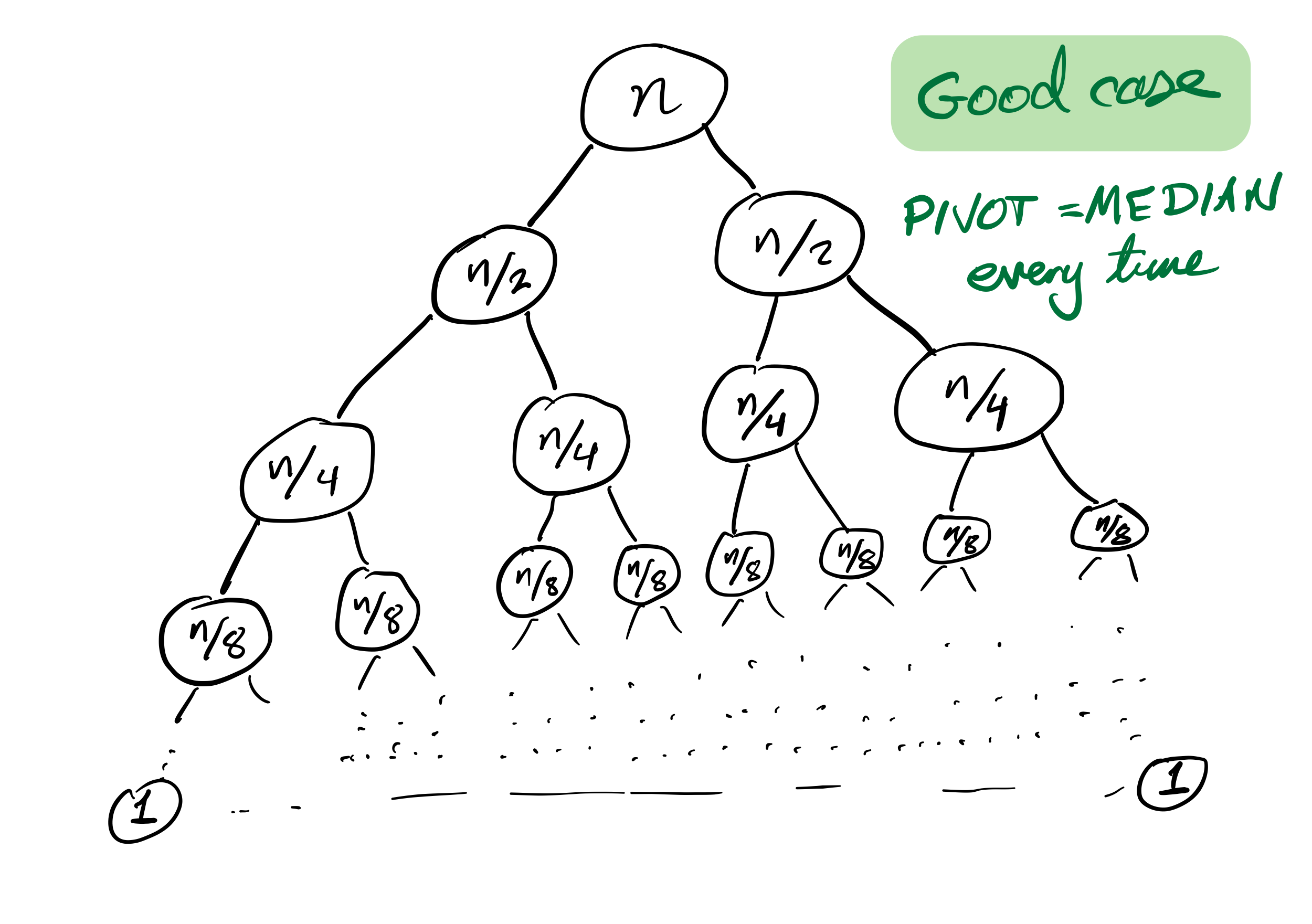

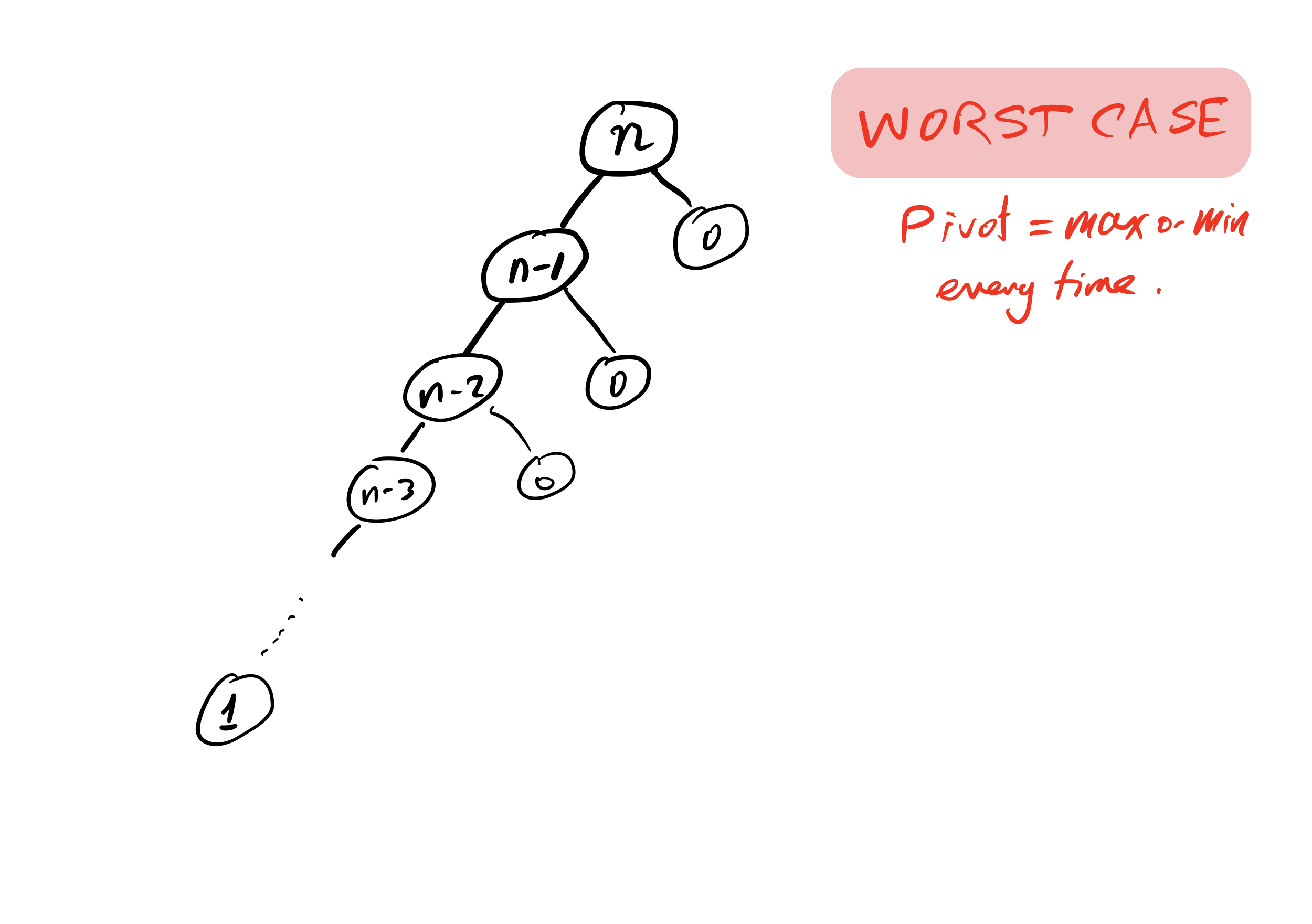
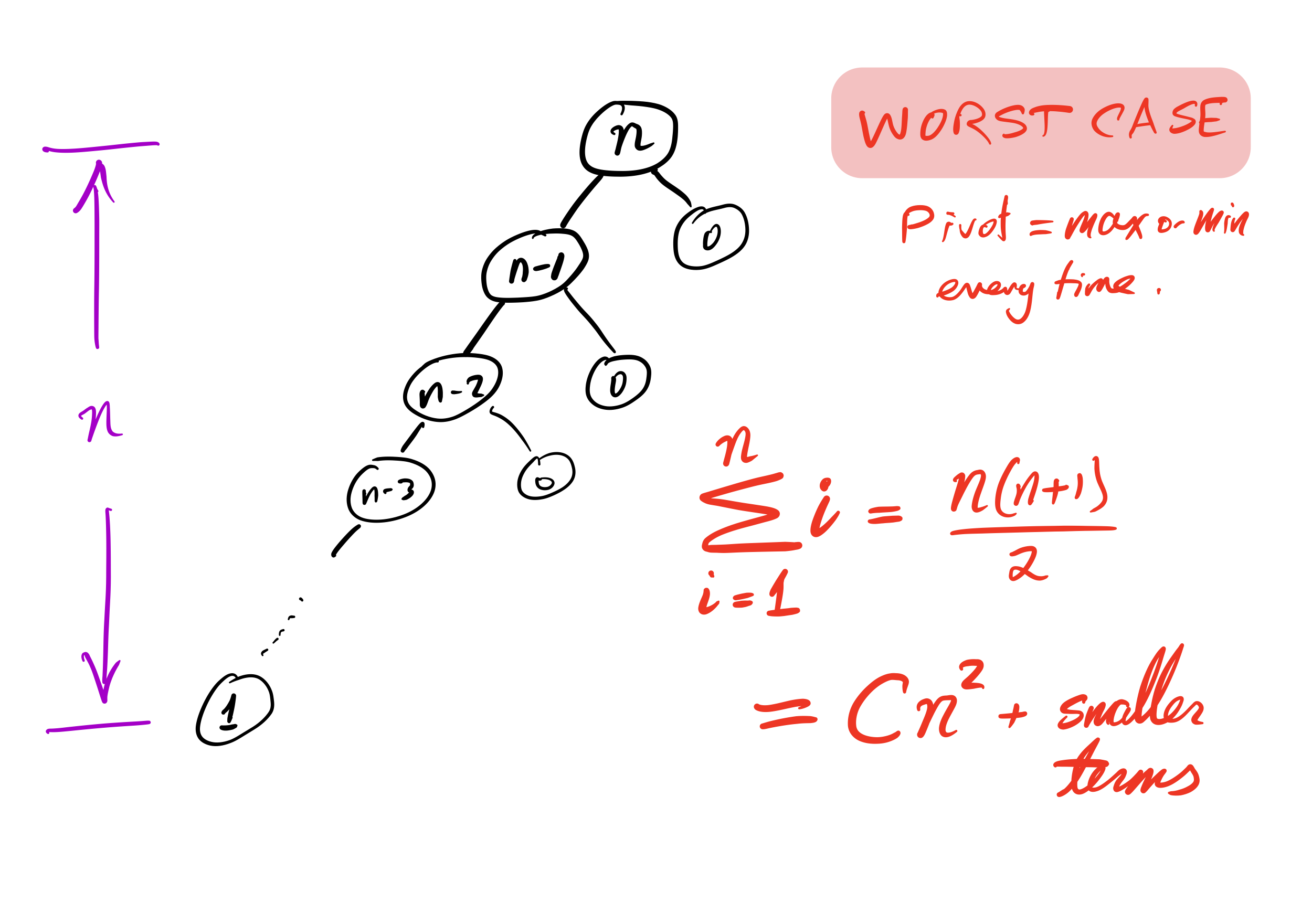
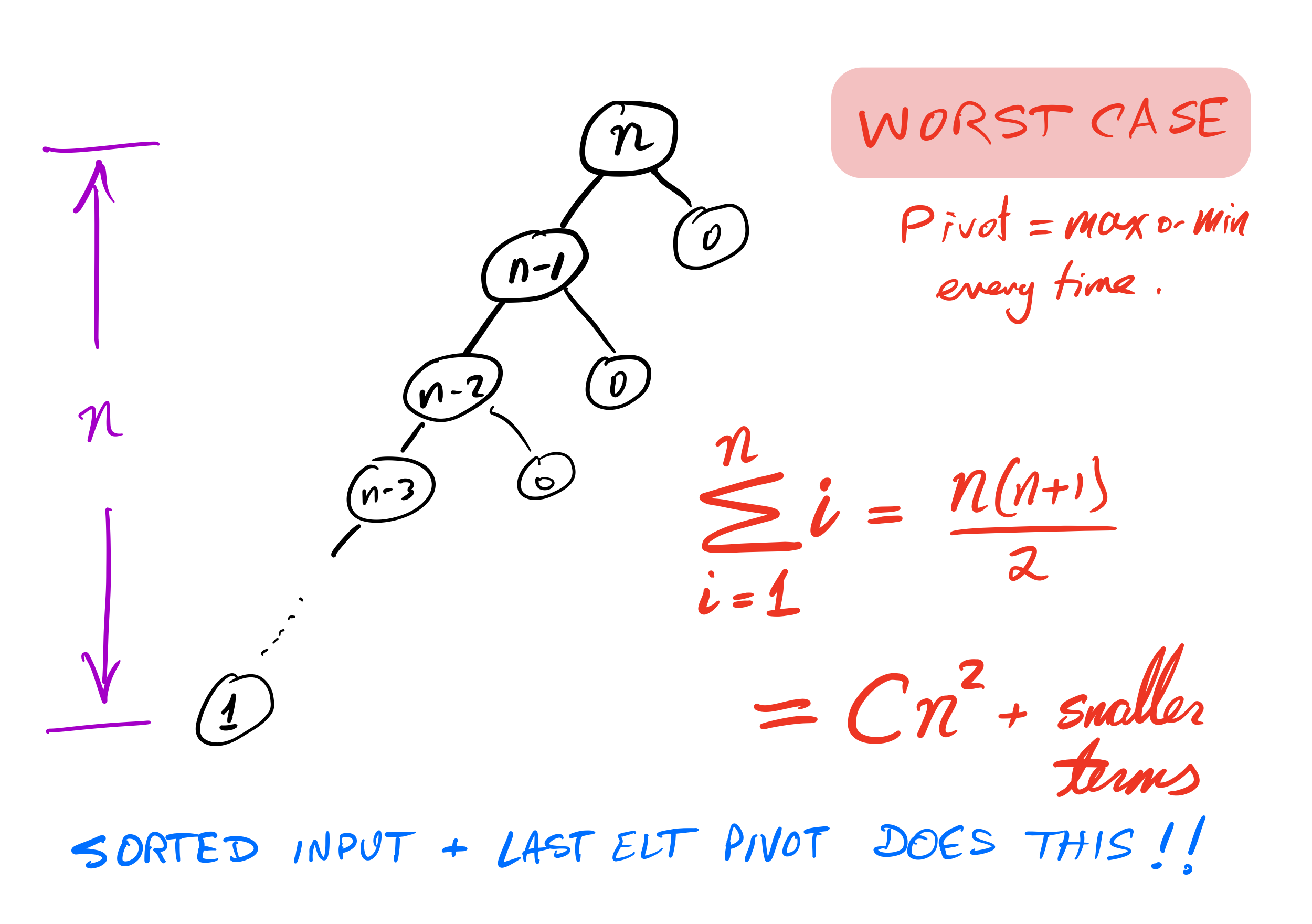
Bad case
What if we ask our version of quicksort to sort a list that is already sorted?
Recursion depth is $n$ (whereas if the pivot is always the median it would be $\approx \log_2 n$).
Number of comparisons $\approx C n^2$. Very slow!
Stability
A sort is called stable if items that compare as equal stay in the same relative order after sorting.
This could be important if the items are more complex objects we want to sort by one attribute (e.g. sort alphabetized employee records by hiring year).
As we implemented them:
- Mergesort is stable
- Quicksort is not stable
Efficiency summary
| Algorithm | Time (worst) | Time (average) | Stable? | Space |
|---|---|---|---|---|
| Mergesort | $C n \log(n)$ | $C n\log(n)$ | Yes | $C n$ |
| Quicksort | $C n^2$ | $C n\log(n)$ | No | $C$ |
(Every time $C$ is used, it represents a different constant.)
Other comparison sorts
- Insertion sort — Convert the beginning of the list to a sorted list, starting with one item and growing by one item at a time.
- Bubble sort — Process the list from left to right. Any time two adjacent items are in the wrong order, switch them. Repeat $n$ times.
Efficiency summary
| Algorithm | Time (worst) | Time (average) | Stable? | Space |
|---|---|---|---|---|
| Mergesort | $C n \log(n)$ | $C n\log(n)$ | Yes | $C n$ |
| Quicksort | $C n^2$ | $C n\log(n)$ | No | $C$ |
| Insertion | $C n^2$ | $C n^2$ | Yes | $C$ |
| Bubble | $C n^2$ | $C n^2$ | Yes | $C$ |
(Every time $C$ is used, it represents a different constant.)
Closing thoughts on sorting
Mergesort is rarely a bad choice. It is stable and sorts in $C n \log(n)$ time. Nearly sorted input is not a pathological case. Its main weakness is its use of memory proportional to the input size.
Heapsort, which we may discuss later, has $C n \log(n)$ running time and uses constant space, but it is not stable.
There are stable comparison sorts with $C n \log(n)$ running time and constant space (best in every category!) though they tend to be more complex.
If swaps and comparisons have very different cost, it may be important to select an algorithm that
minimizes one of them. Python's list.sort assumes that comparisons are expensive, and
uses Timsort.
Quadratic danger
Algorithms that take time proportional to $n^2$ are a big source of real-world trouble. They are often fast enough in small-scale tests to not be noticed as a problem, yet are slow enough for large inputs to disable the fastest computers.
E.g. the Accidentally Quadratic blog collects examples found (and usually fixed) in real-world software.
References
- An algorithms textbook like Algorithms by Jeff Erickson will discuss analysis of running time for sorting algorithms in more depth.
Revision history
- 2023-02-17 Finalization of the 2023 lecture this was based on
- 2024-02-09 Initial publication