Lecture 15

Trees

MCS 275 Spring 2024
Emily Dumas

Lecture 15: Trees

Reminders and announcements:

• Project 2 will be posted today, discussion Wednesday
• Project 1 grading underway
• Homework 5 due tomorrow at Noon

We've talked about some recursive algorithms.

Now let's think about recursive data structures.

Graphs

In mathematics, a graph is a collection of nodes (or vertices) and edges (which join pairs of nodes).

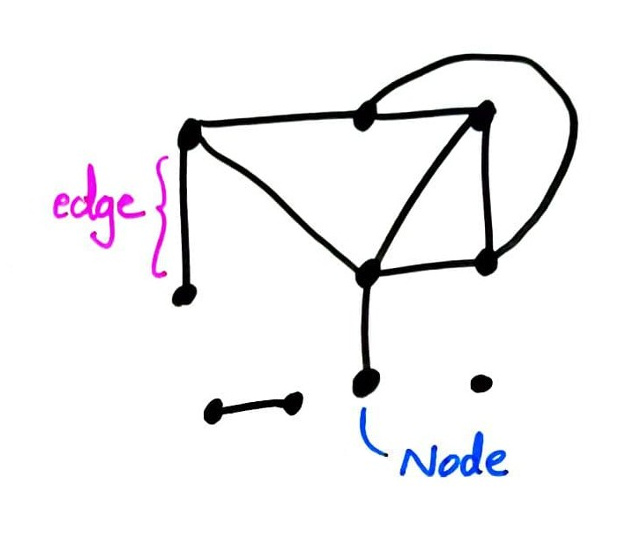
Connectivity

A graph is connected if every pair of nodes can be joined by at least one path.

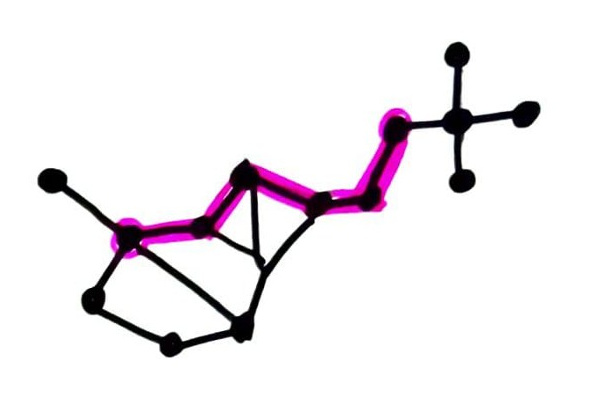
Connectivity

A graph is connected if every pair of nodes can be joined by at least one path.

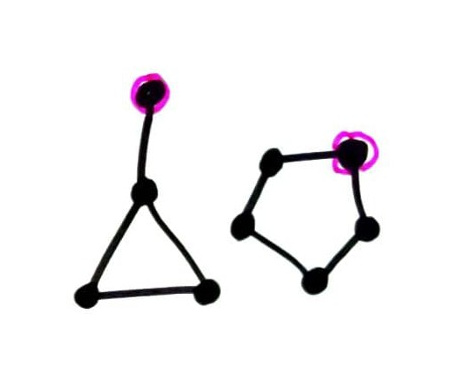
Tree

A tree is a graph where every pair of nodes can be joined by exactly one path (no more, no less).

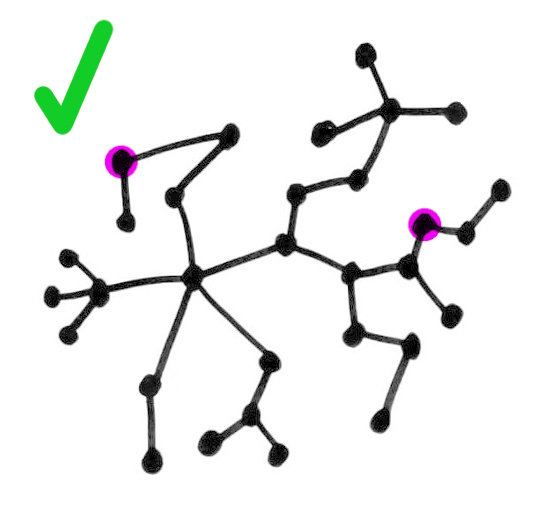
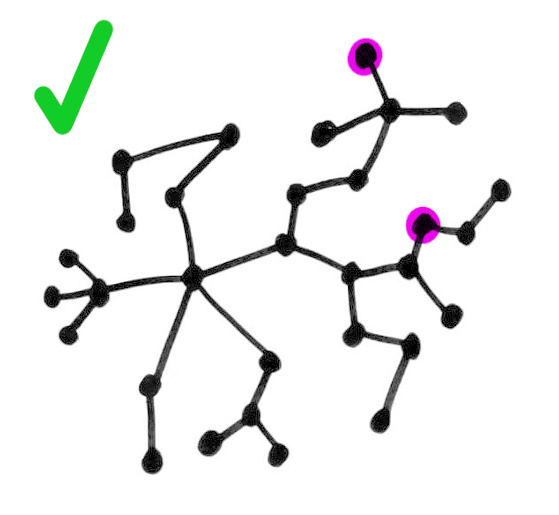
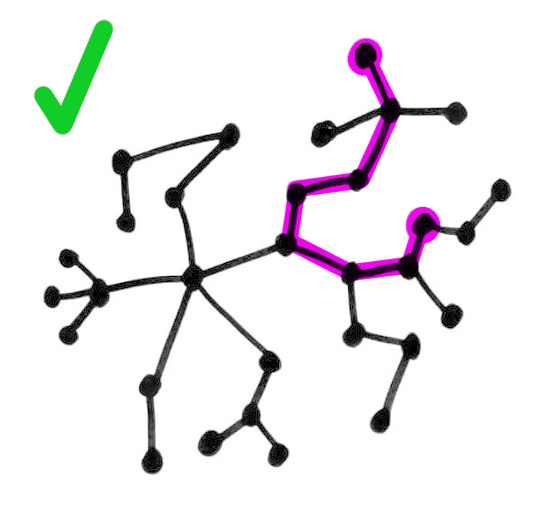
Tree

A tree is a graph where every pair of nodes can be joined by exactly one path (no more, no less).

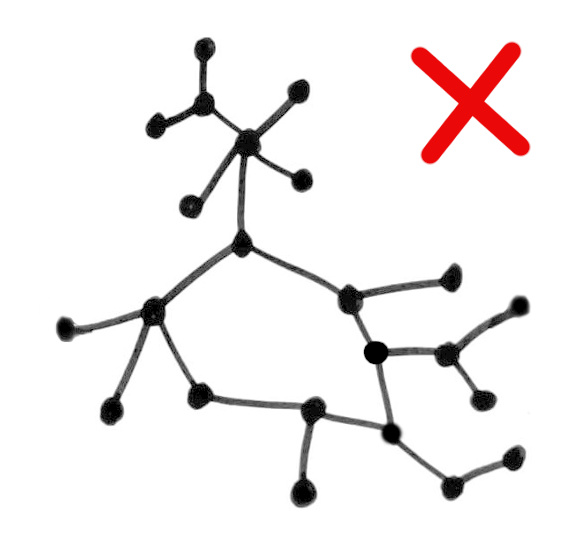
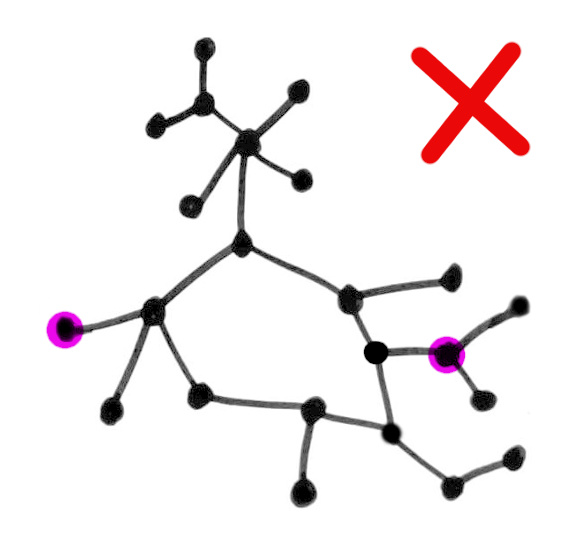
Equivalently, a tree is a connected graph with no loops.

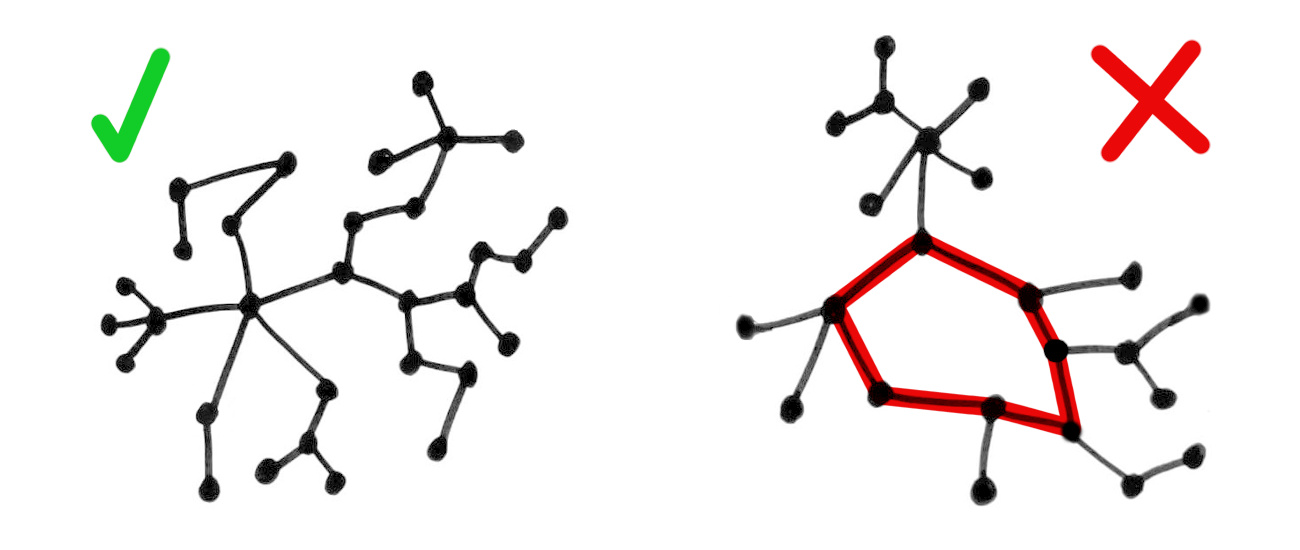
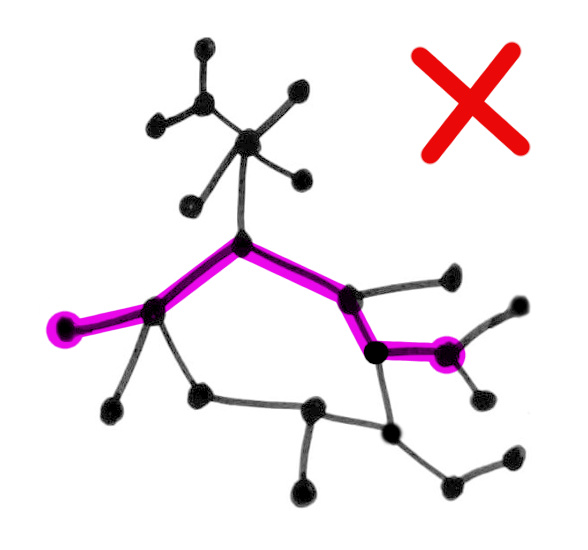
Equivalently, a tree is a connected graph that becomes disconnected if any edge is removed.

(Exercise: Prove this is an equivalent definition!)

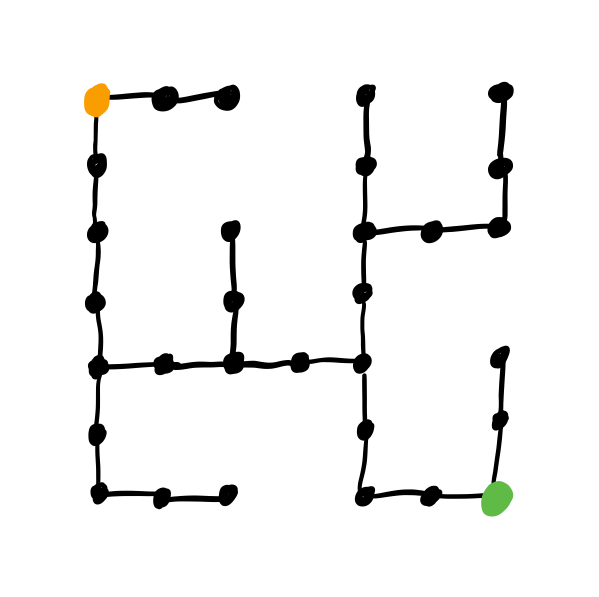
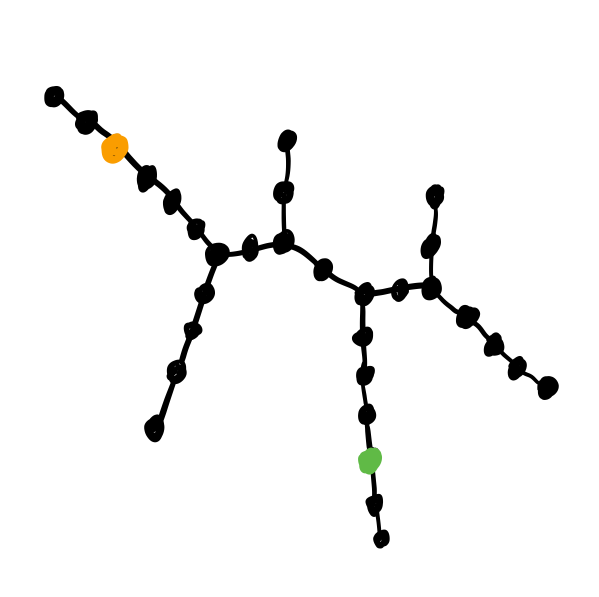
Example

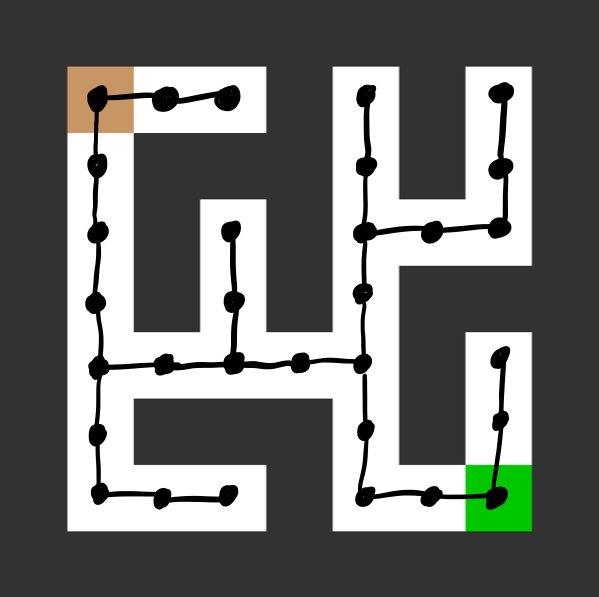
The random mazes produced by maze.PrimRandomMaze(...) can be seen as trees, with the the open squares as nodes and edges for x/y neighbors.

Example

Roots and directions

The trees considered in CS usually have one node distinguished, called the root.

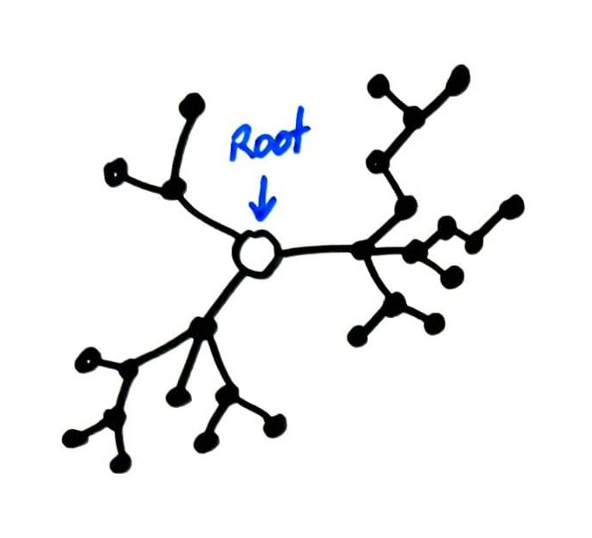
There's nothing special about the root except that it is labeled as such. Any node of a tree could be chosen to be its root node.

Such rooted trees are usually drawn with the root at top

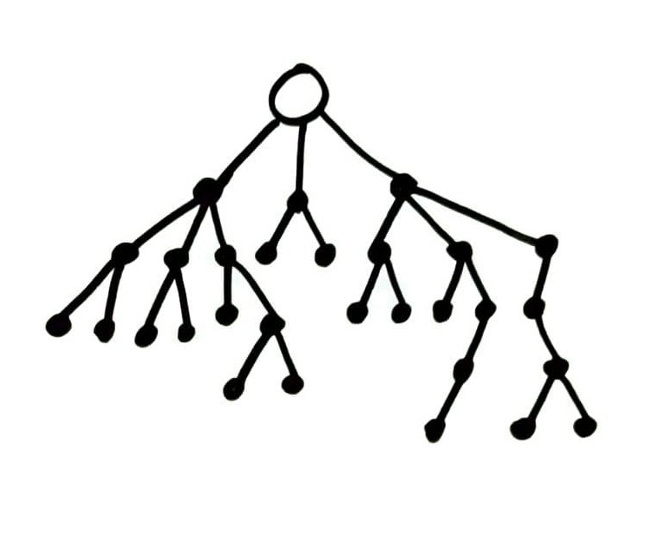
and vertices farther from the root successively lower.

Surely this convention is inspired by nature

That maze again

Choosing a root lets us orient all of the edges so they point away from it.

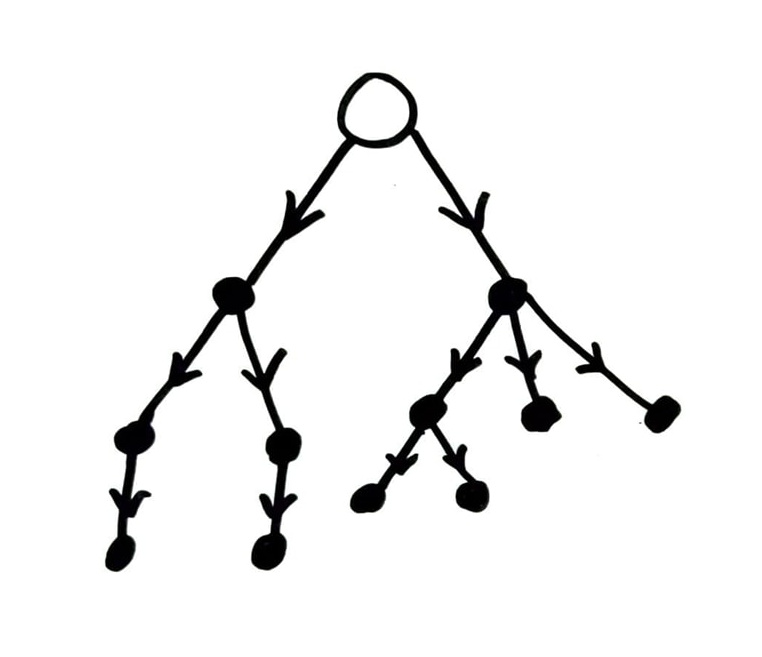
Hence the usual way of drawing a tree will have these arrows pointing downward.

Each node (except the root) has an incoming edge, from its parent (closer to the root).

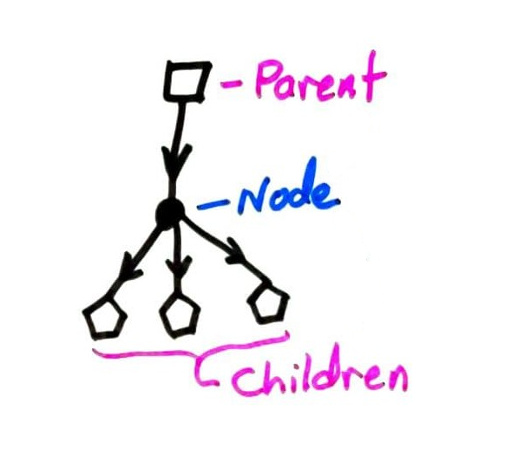
Each node may have one or more outgoing edges, to its children (farther from the root).

Binary trees

In CS, a binary tree is a (rooted) tree in which every node has ≤ 2 children, labeled "left" and "right".

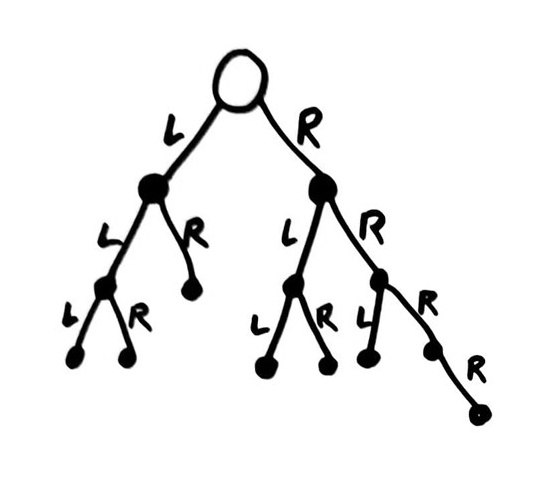
Horizontal relative position is used to indicate this labeling, rather than explicitly writing it on the edges.

Binary trees

In CS, a binary tree is a (rooted) tree in which every node has ≤ 2 children, labeled "left" and "right".

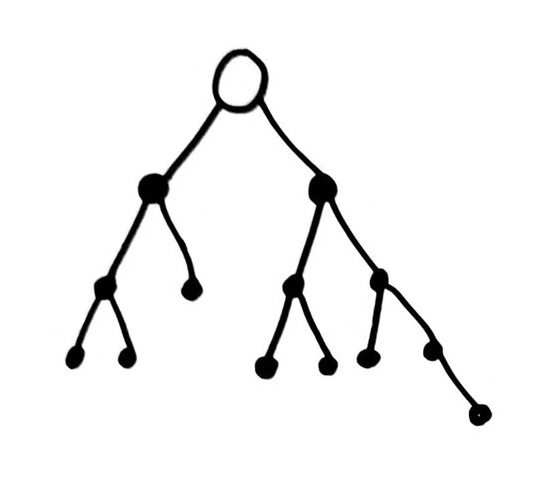
Horizontal relative position is used to indicate this labeling, rather than explicitly writing it on the edges.

Representation

How can we store a tree in Python?

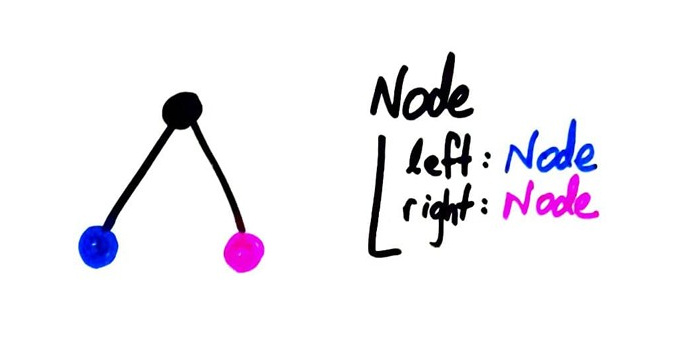
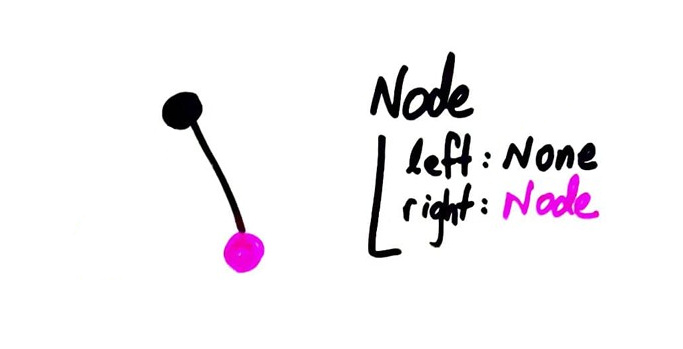
Make a class Node, with attribues left and right that can be None or other Node objects.

Then a single Node gives us access to the entire tree below it.

Why?

We can also store additional information in the nodes of a binary tree. If present, this is called the key or value or cargo of a node.

This turns out to be a very efficient data structure for many purposes. A lot of data can be accessed in a few steps from the root node.

Binary tree

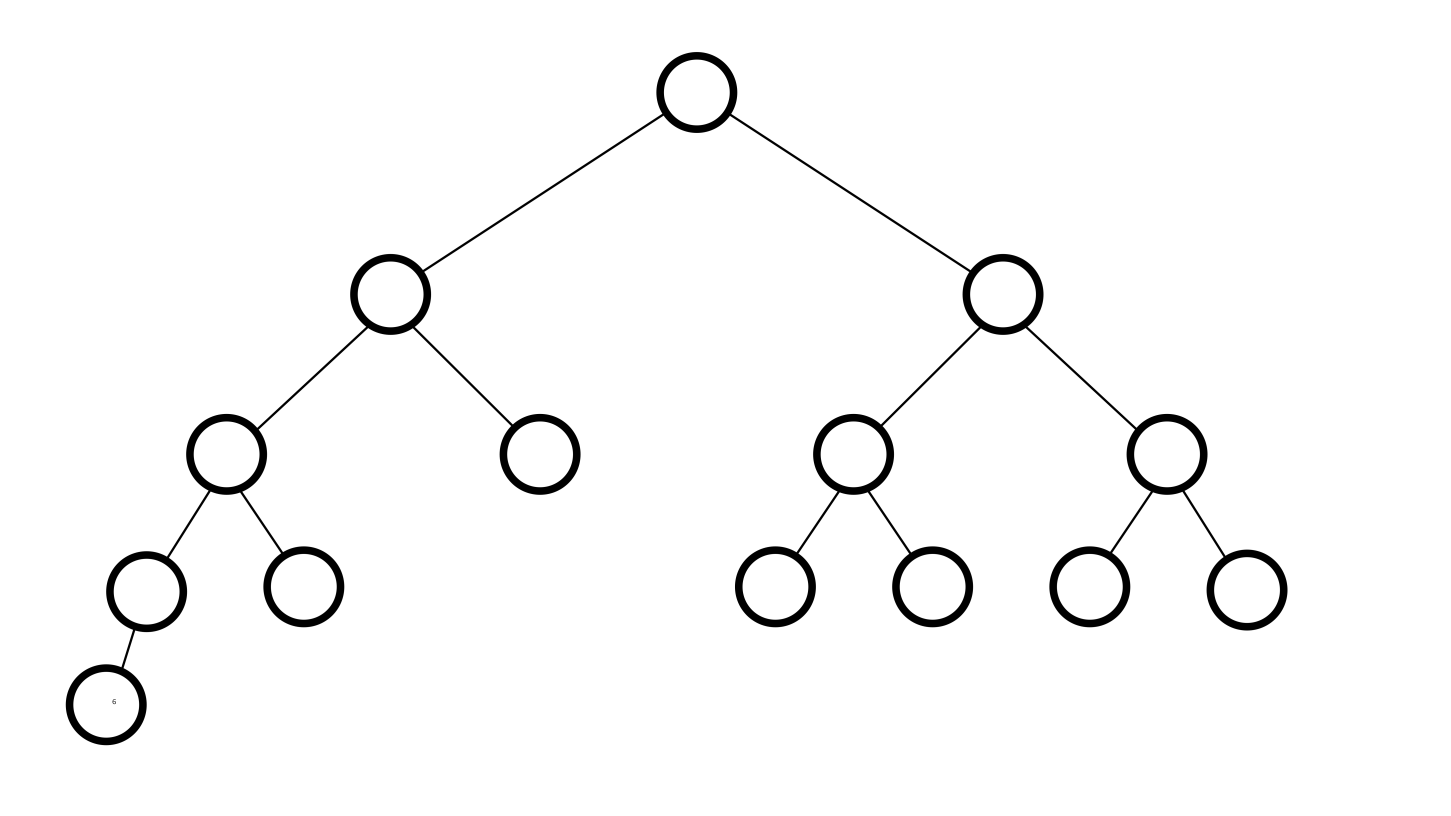
Binary tree with keys

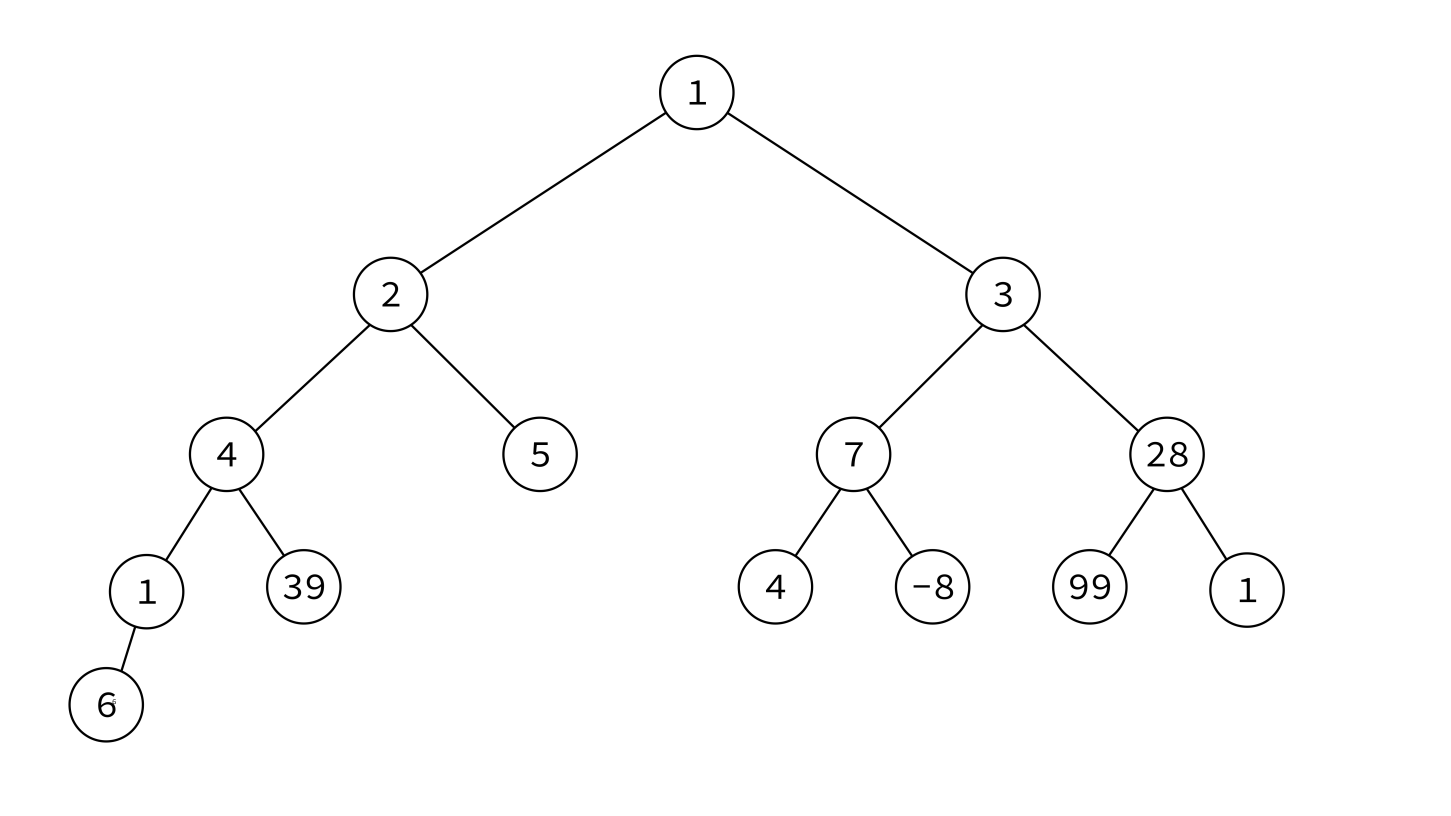
Binary tree with keys

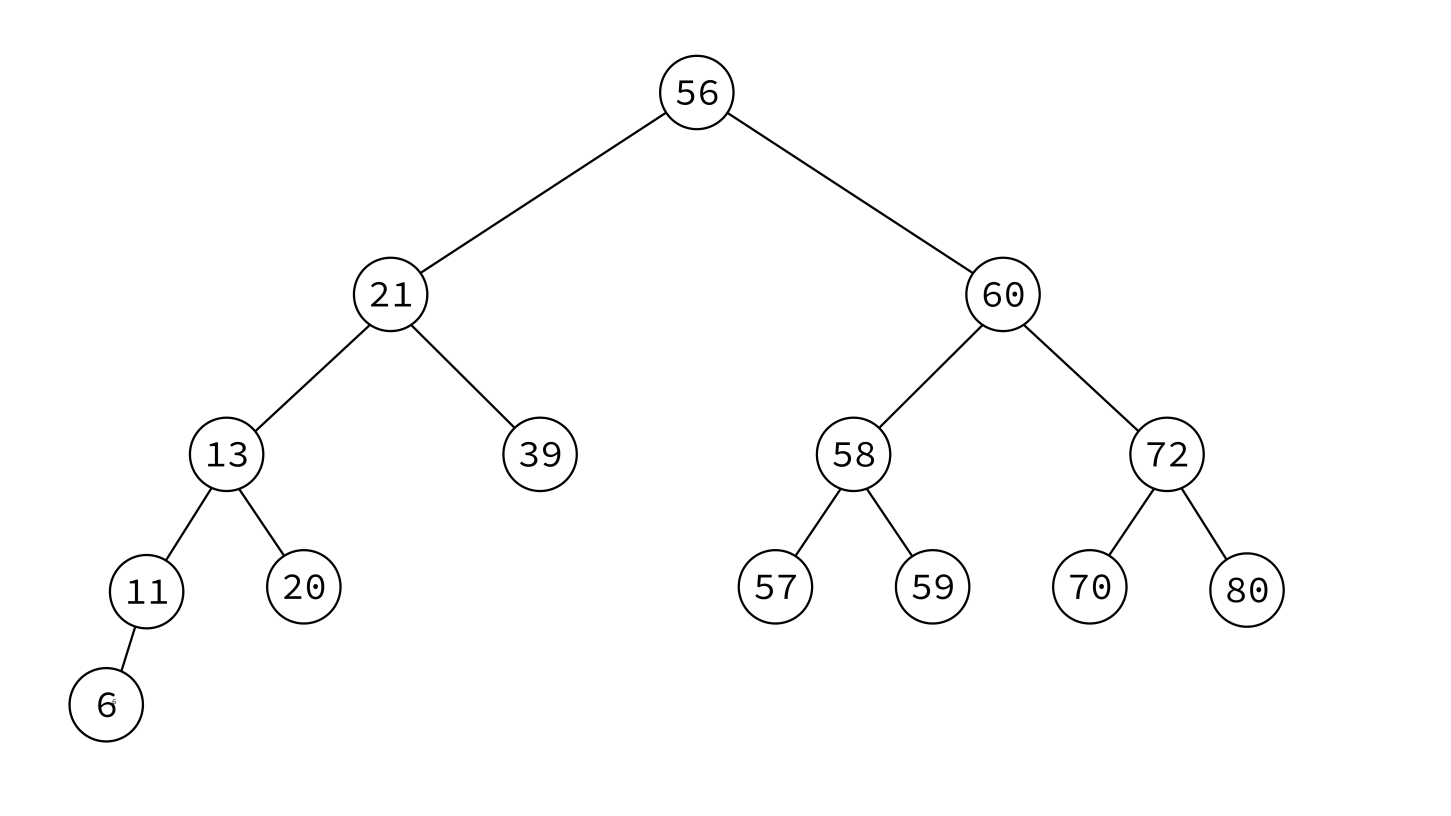
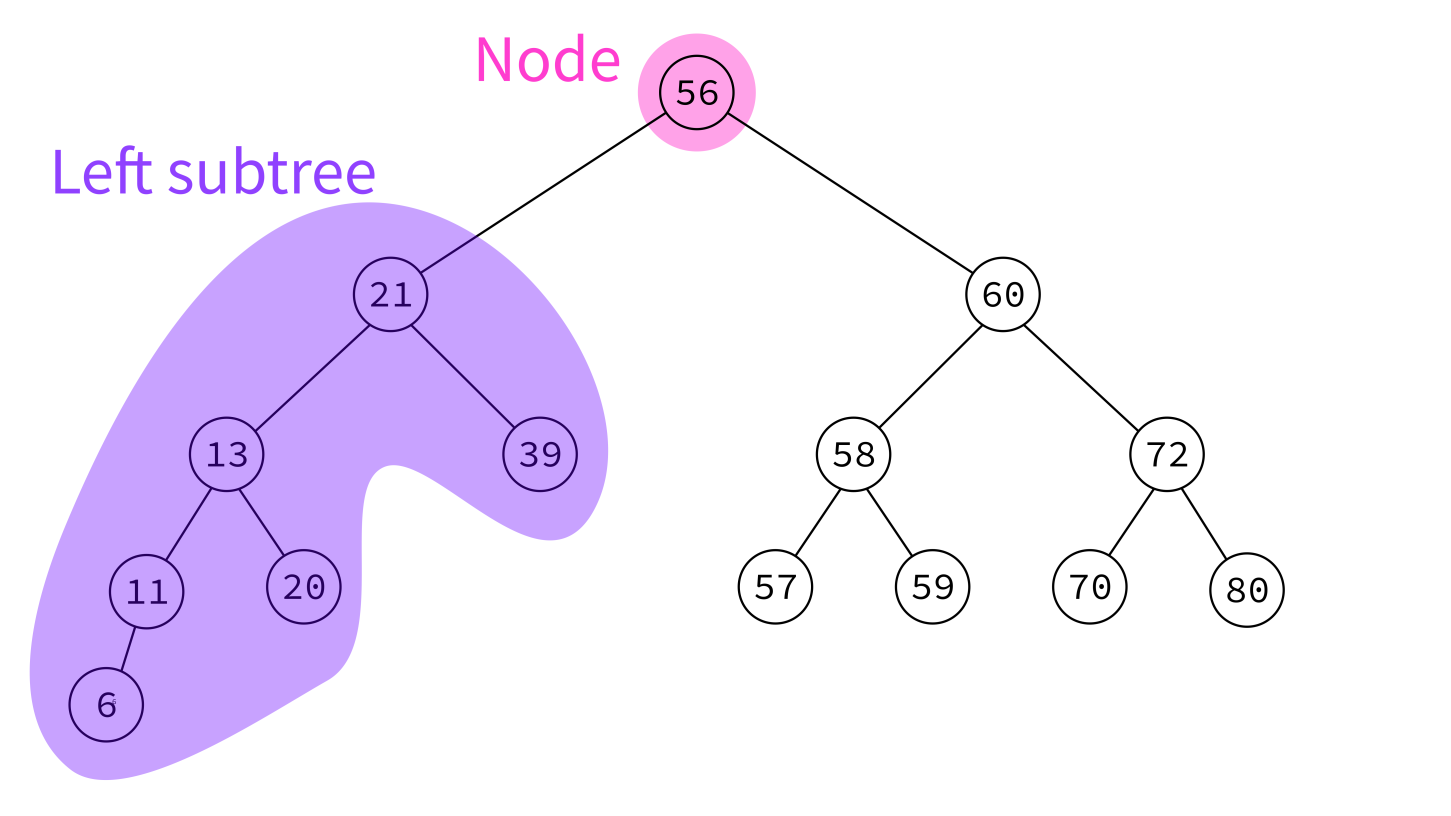
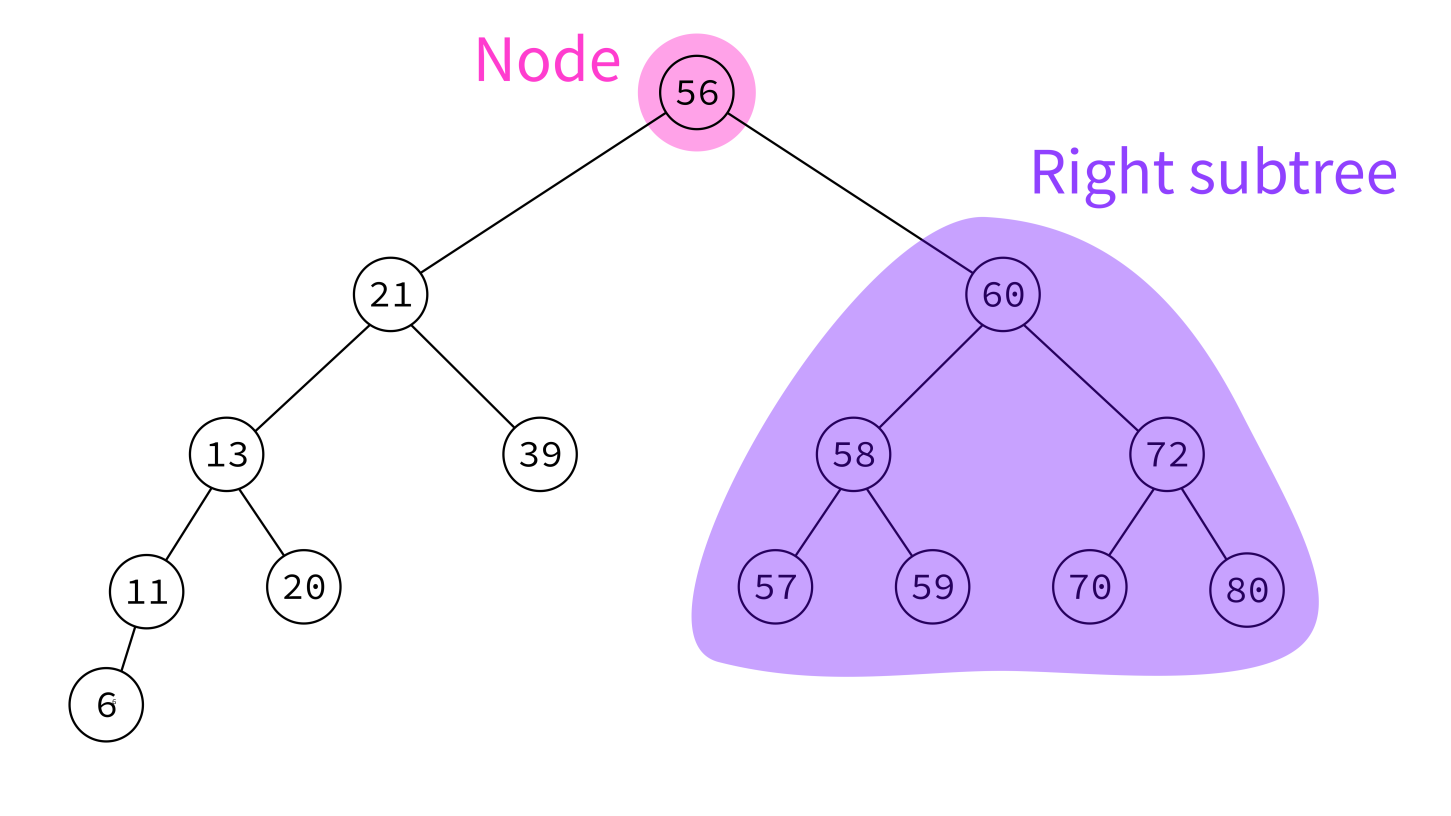
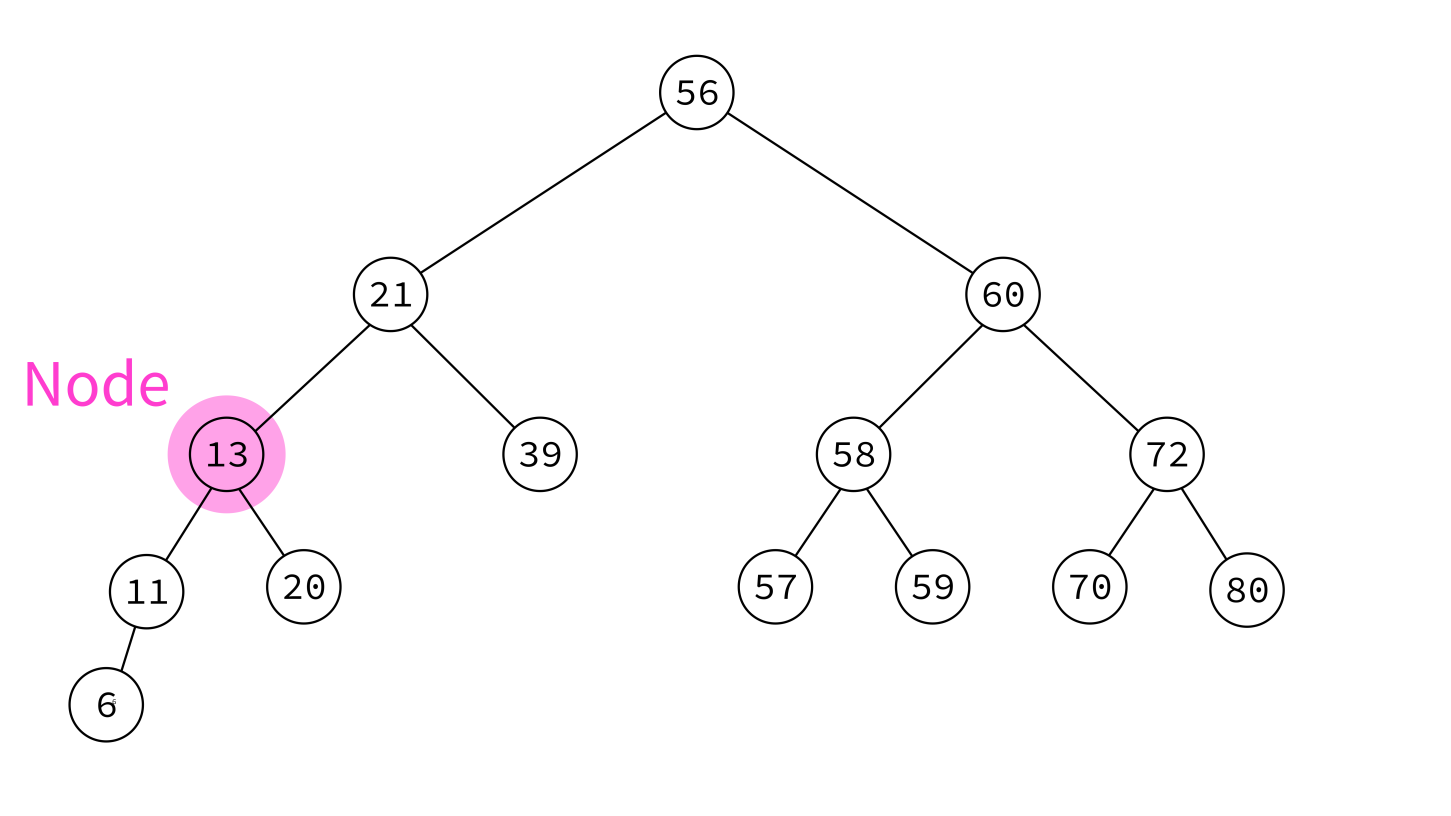
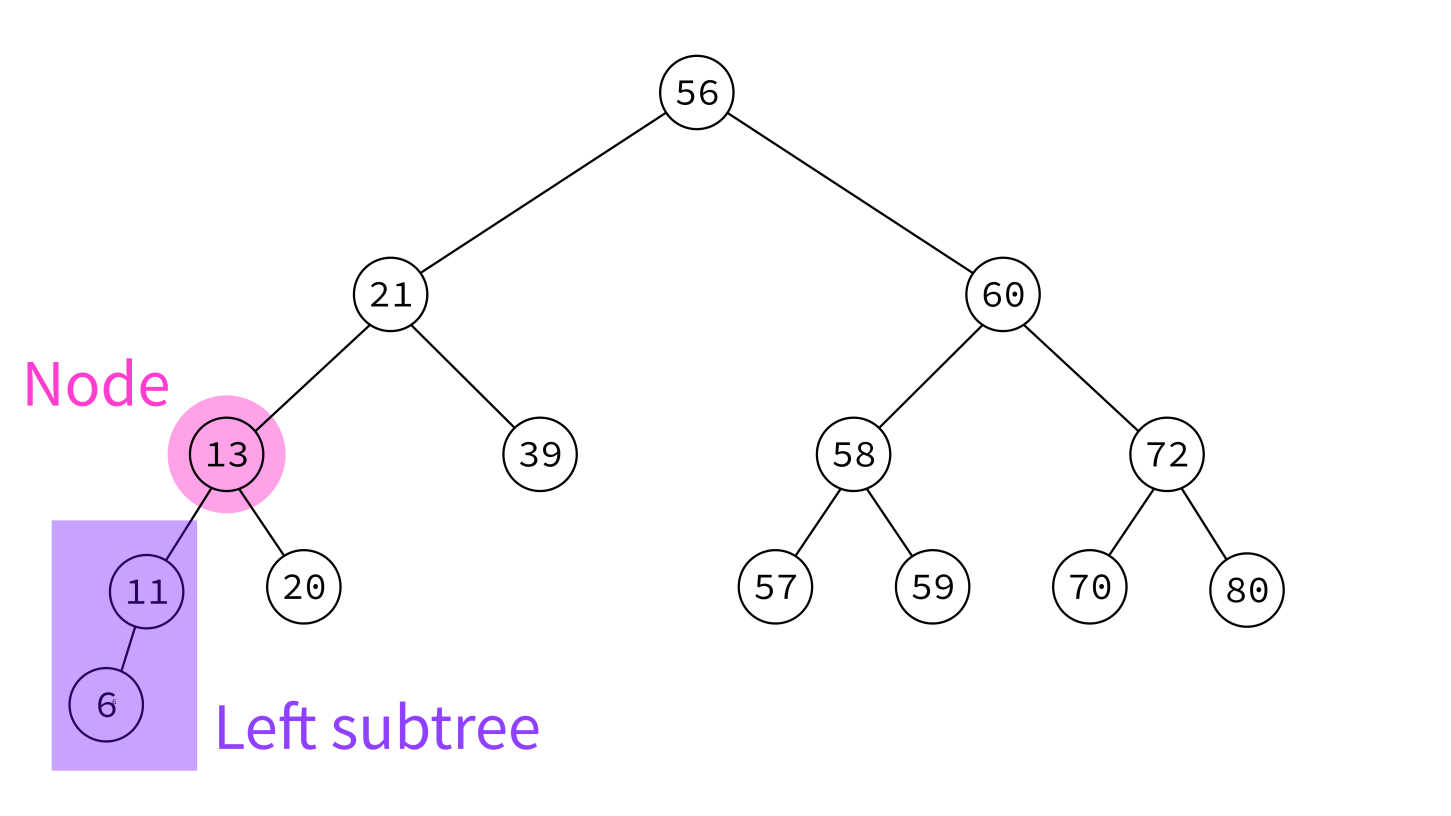
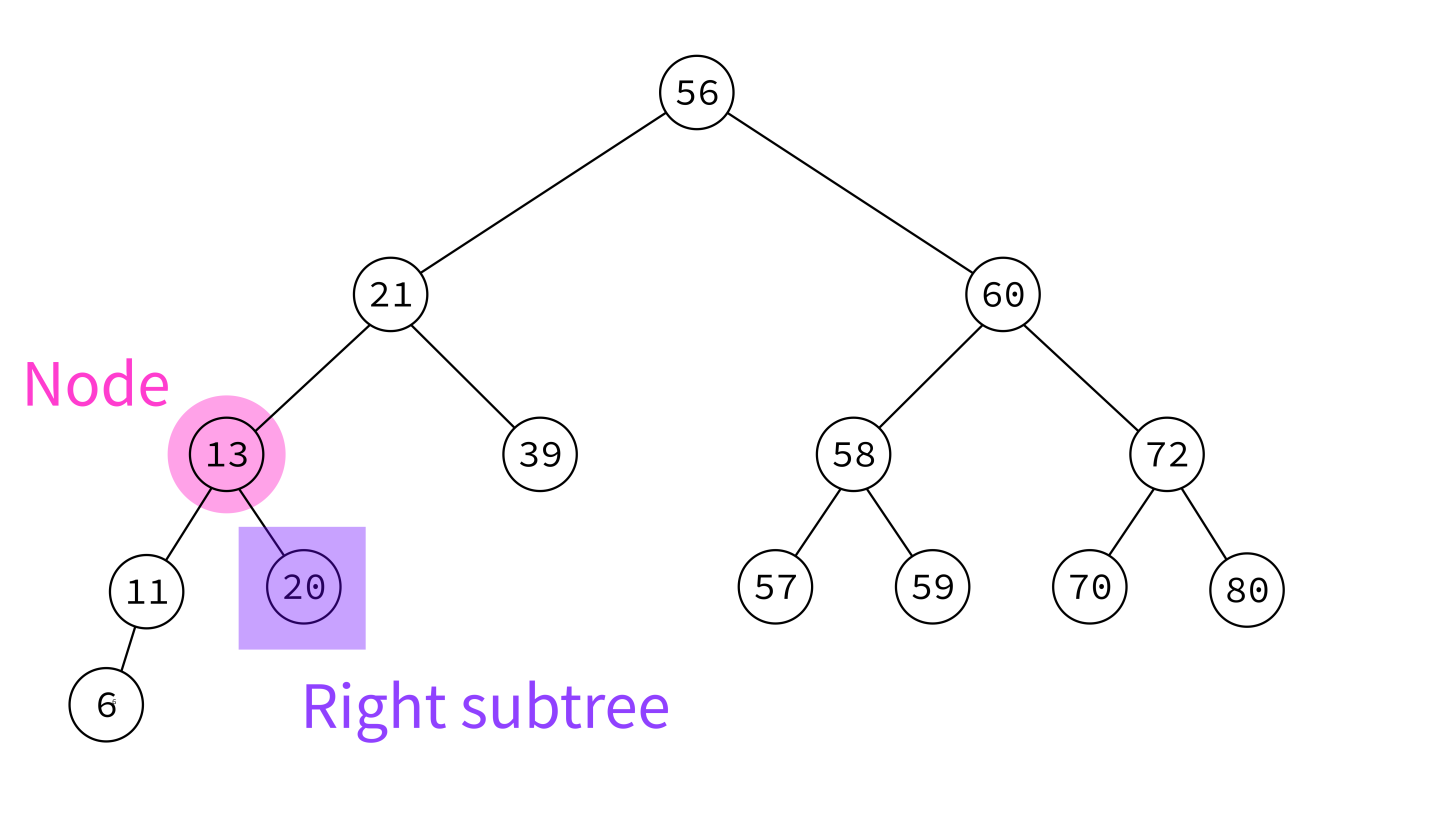
Binary search tree

Binary search tree

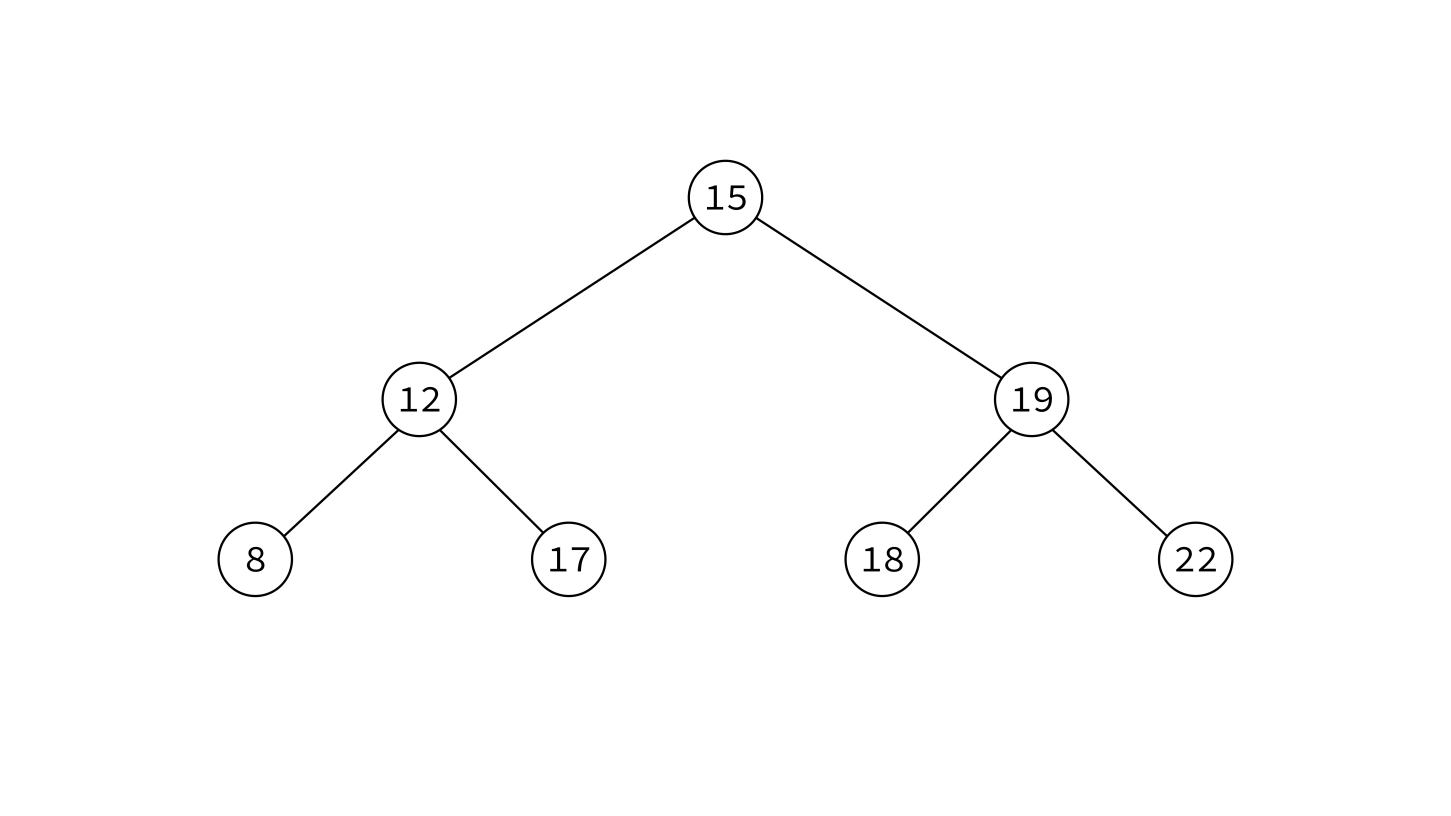
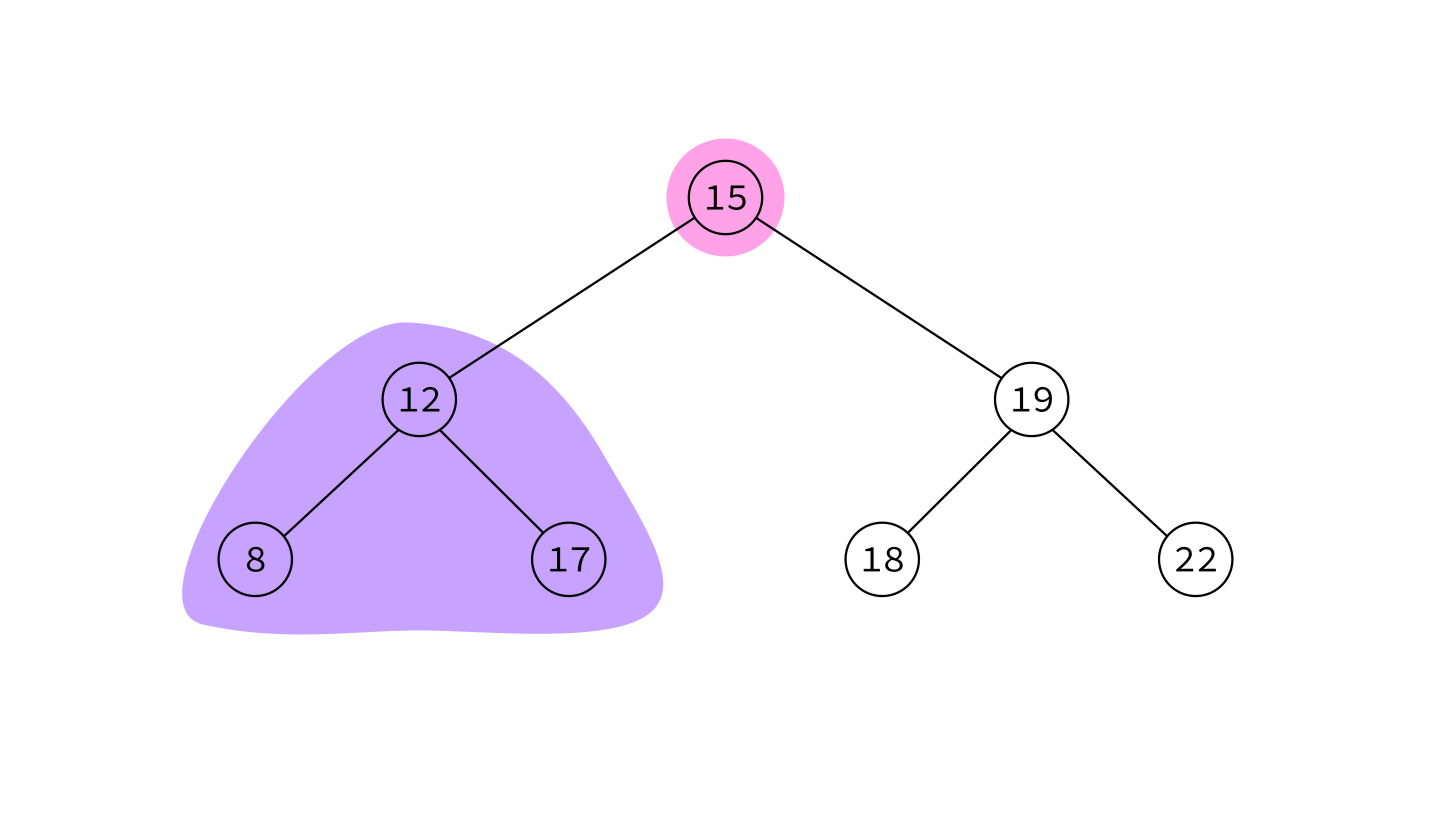
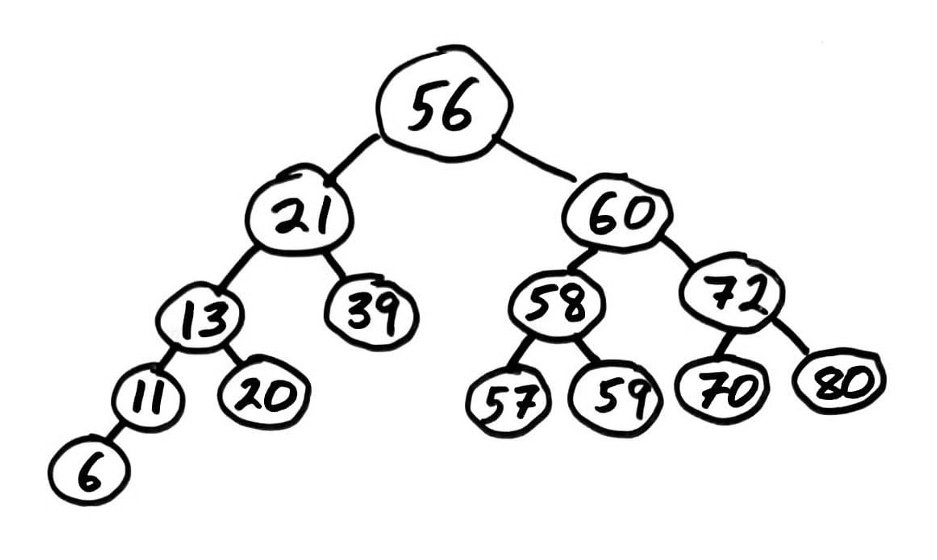
A binary search tree (BST) is a binary tree with keys that can be compared, such that for each node:

• Left subtree contains only smaller keys
• Right subtree contains only greater keys

NOT a BST

This "just" is a binary tree with keys.

This allows a natural way to check if a value is present with a game of "too high / too low".

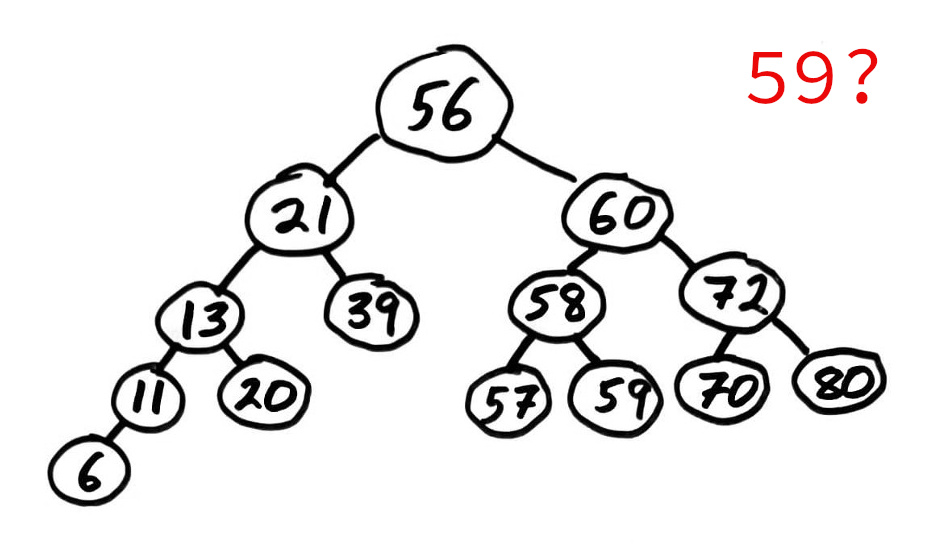
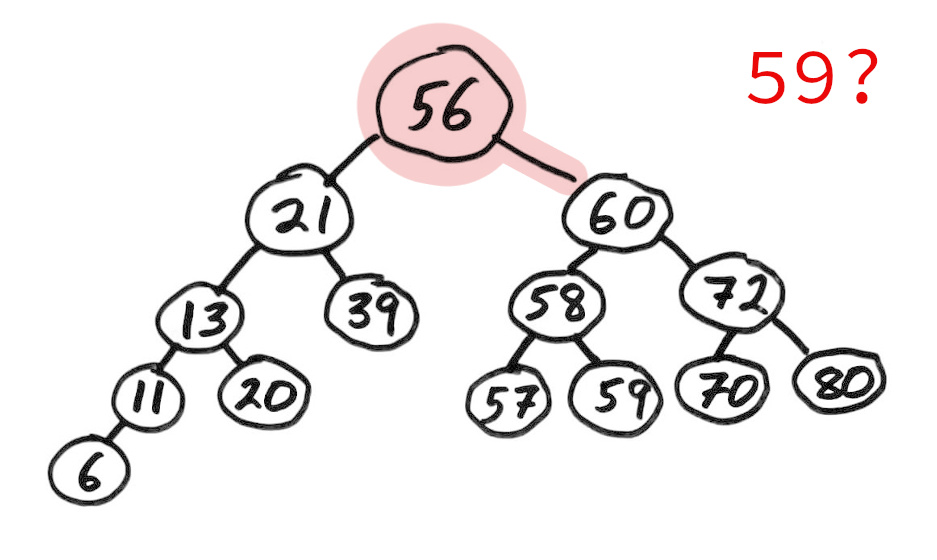
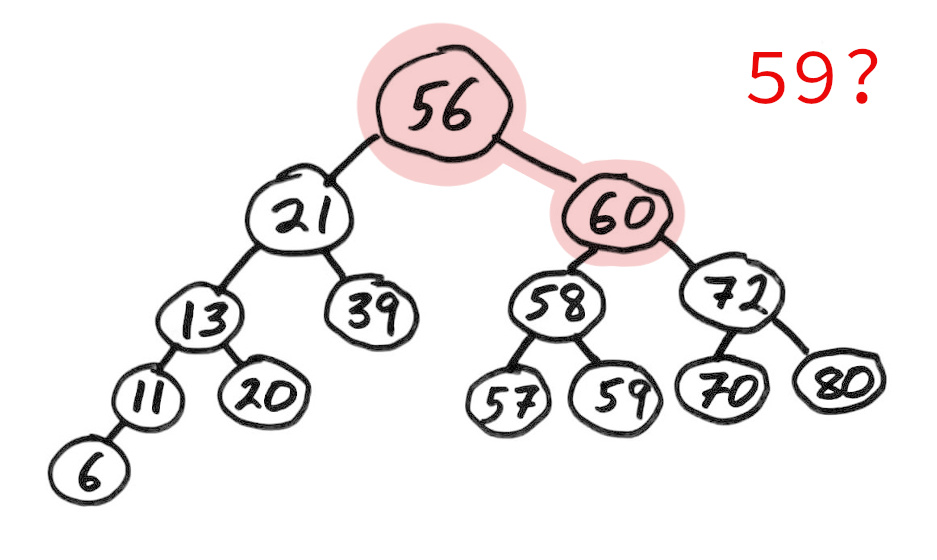
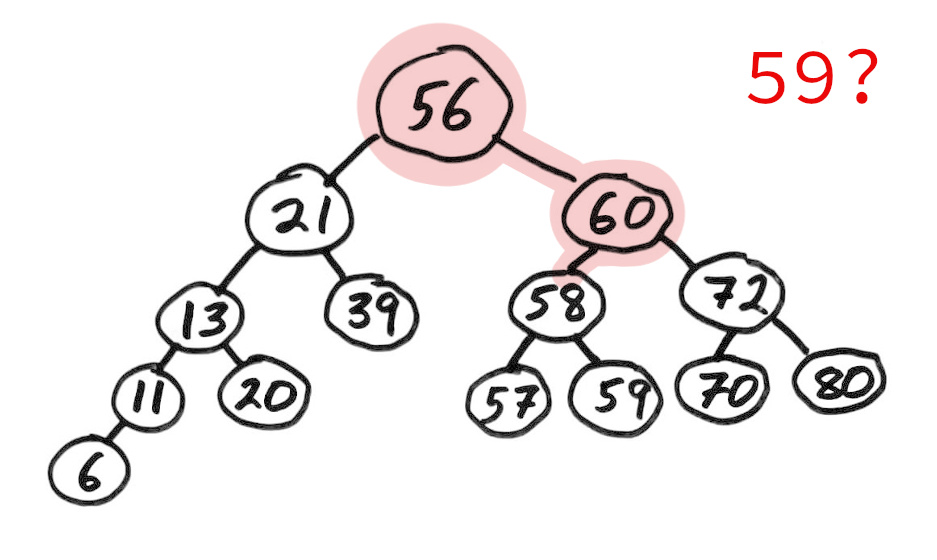
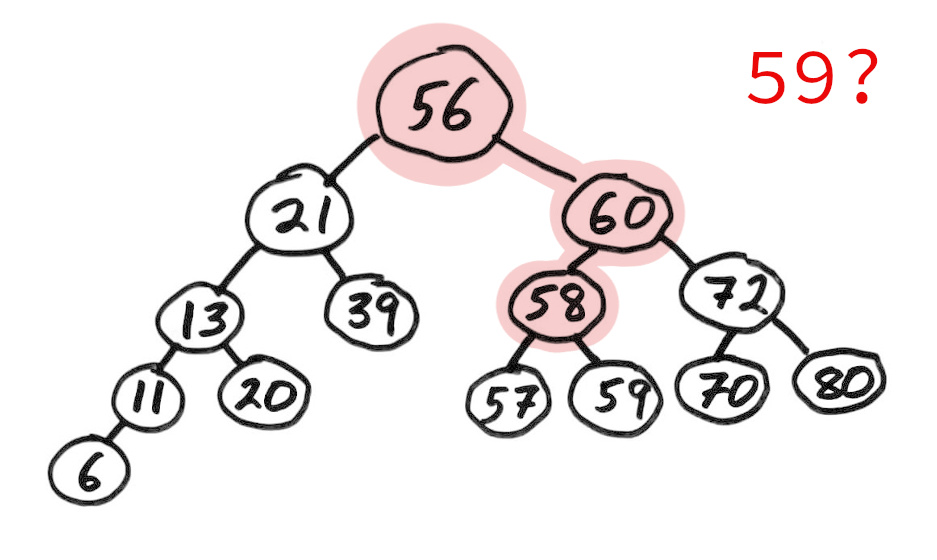
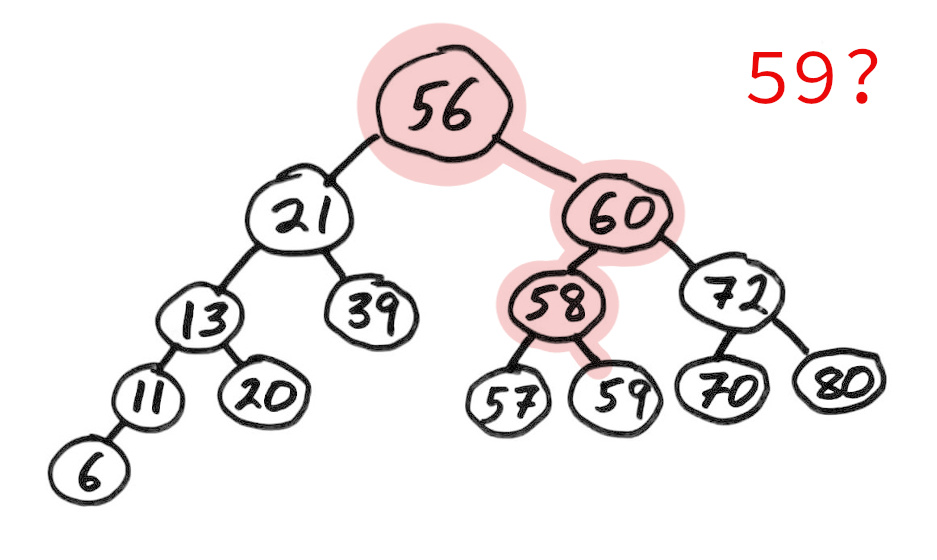
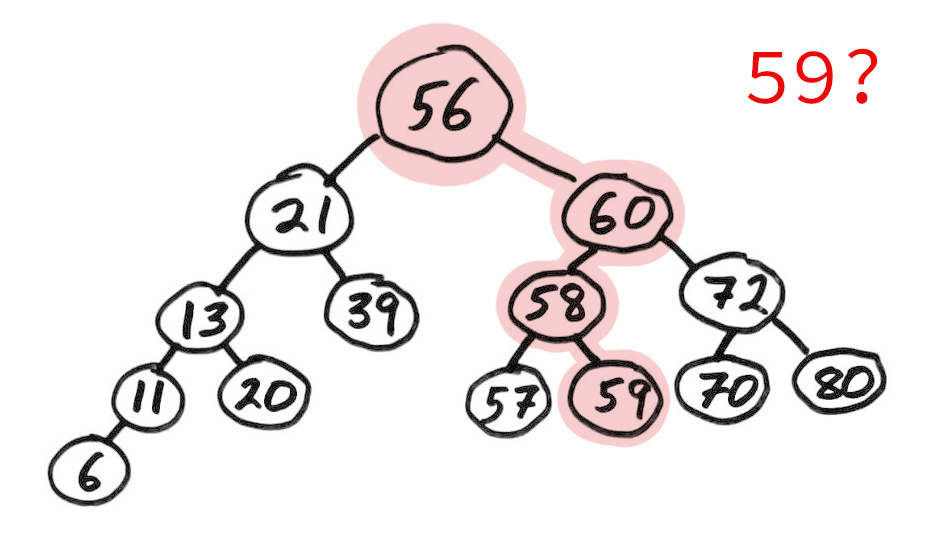
Notice that searching a BST is naturally a simple recursion!

While for a general binary tree with keys the best we can do is recursion with backtracking.