Lecture 9
Recursion vs Iteration
MCS 275 Spring 2024
Emily Dumas
Lecture 9: Recursion vs Iteration
Reminders and announcements:
- Homework 3 due Tuesday at Noon
- Project 1 posted
- Project 1 due Fri Feb 9 at 11:59pm
Project 1 discussion
📦📦📦 → 🚛
- Based on factory logistics scenario.
- Object-oriented program provided.
- You add subclasses with prescribed behavior.
Full details in the project description.
Where we left off
Recursive function examples:
- Factorial
- Fibonacci sequence
- Paper-folding sequence
Iterative solutions
Let's write functions that compute the same things, but using iteration (loops) instead of recursion.
Timing comparison
Let's compare the running time of the iterative and recursive solutions.
Question
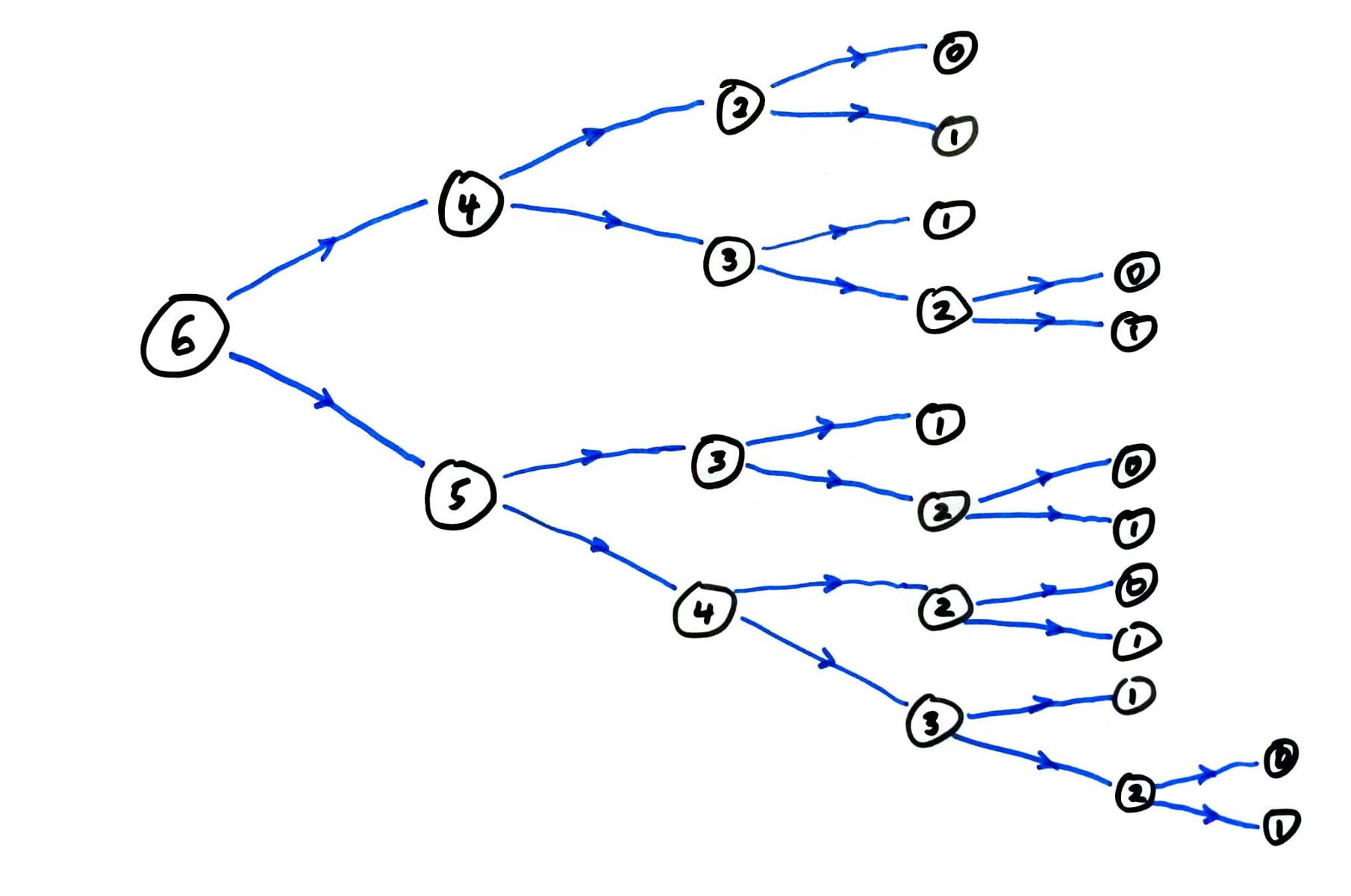
Why is recursive fact() somewhat competitive, but fib() is dreadfully slow?
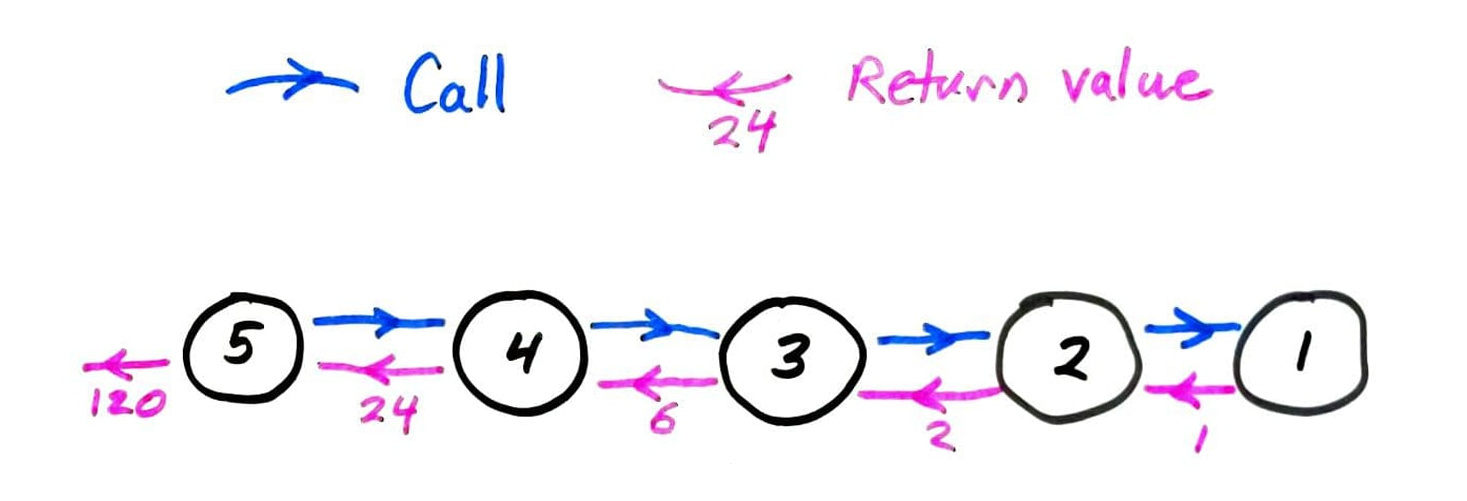
Let's track the number of function calls.
fact call graph


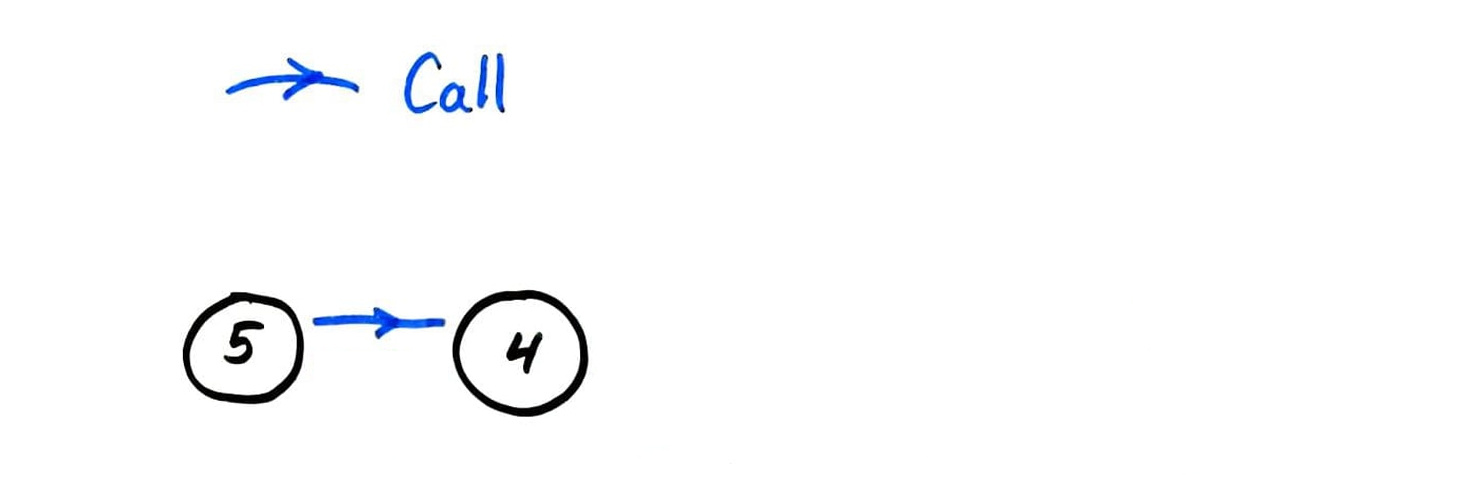
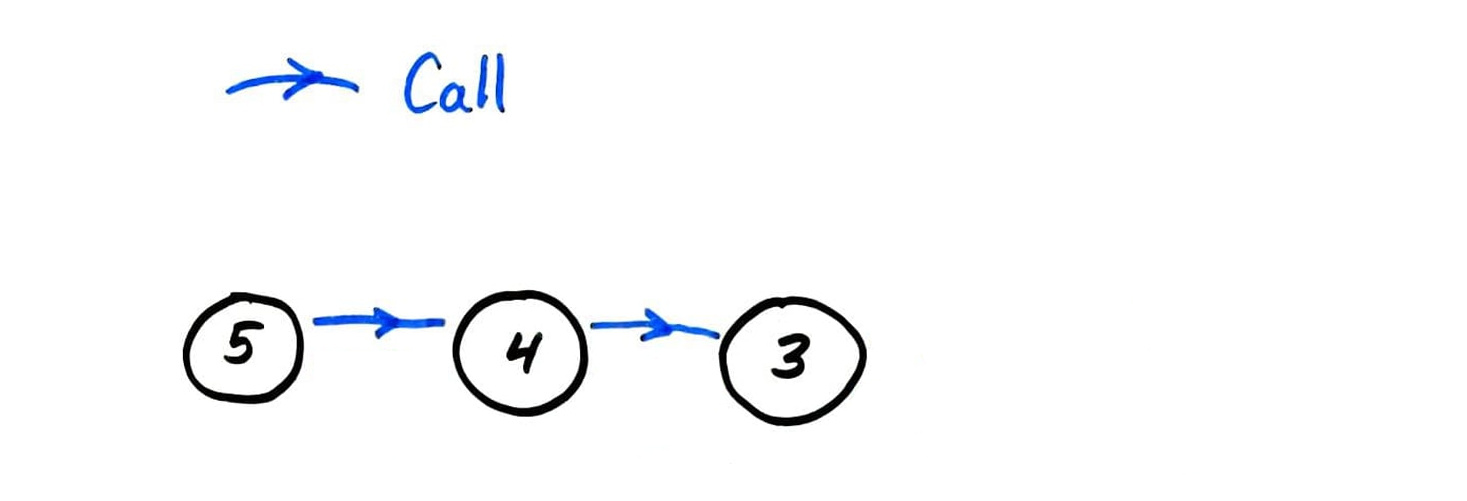
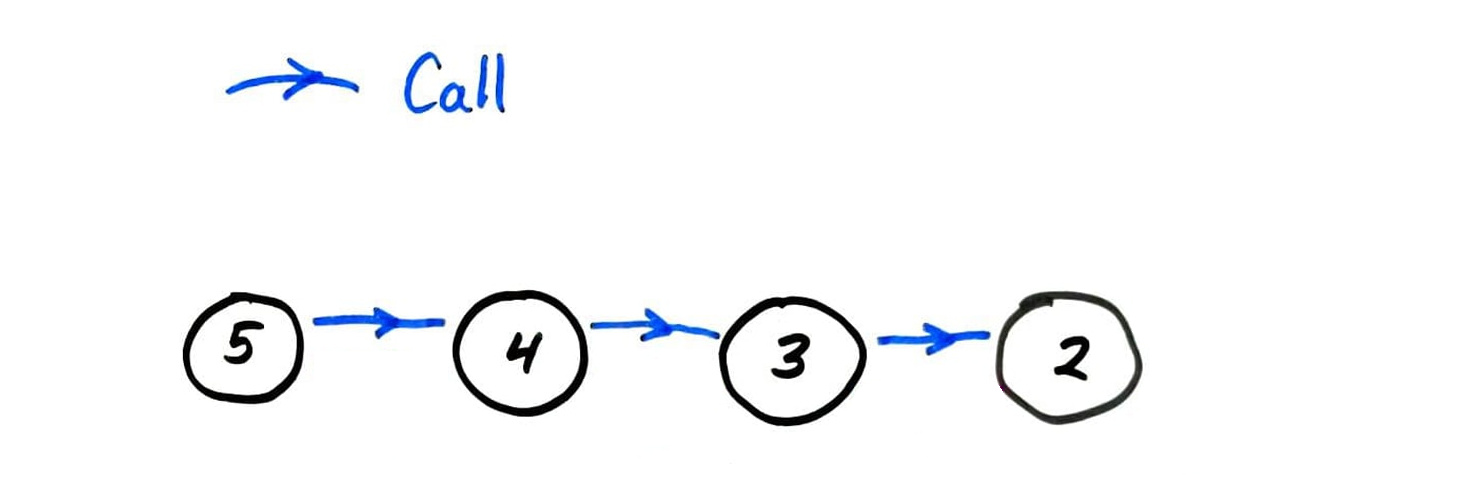
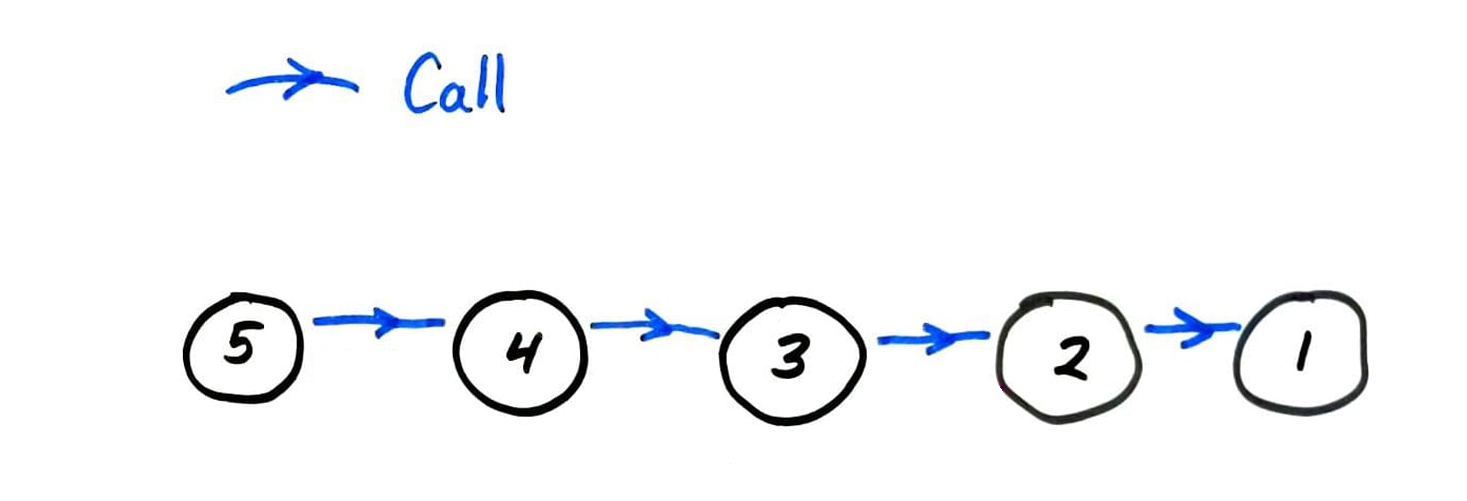
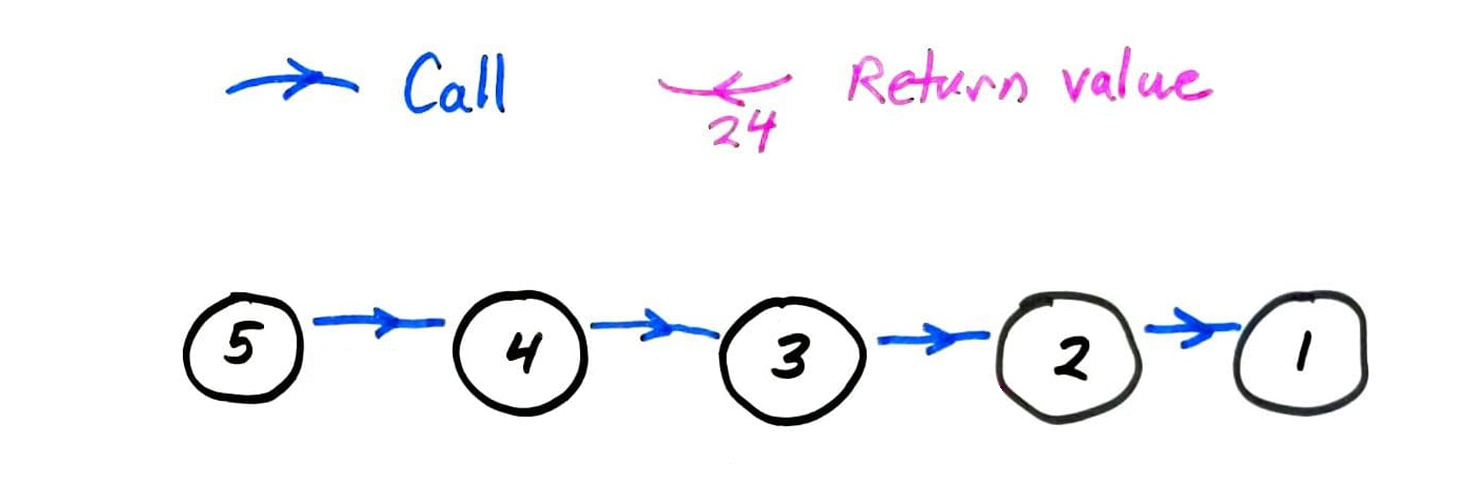
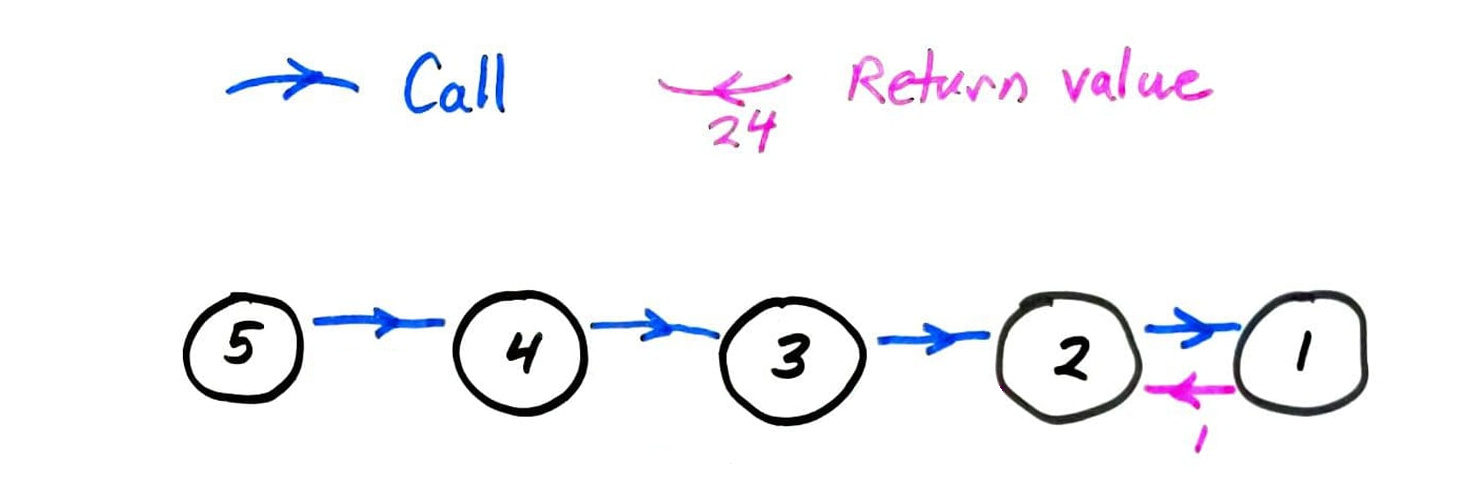
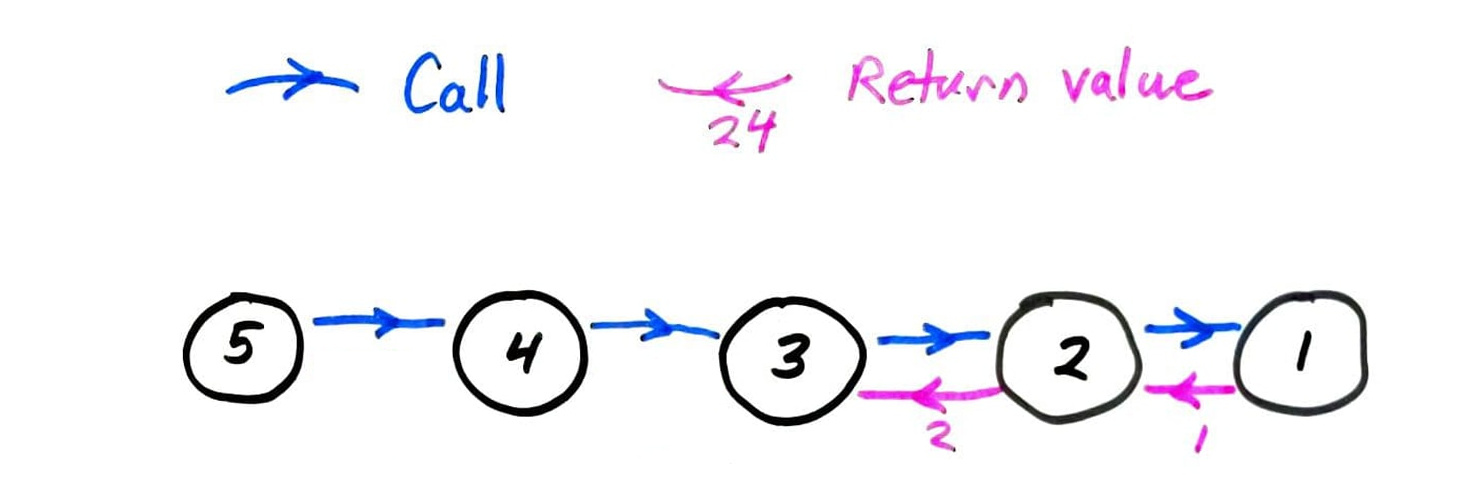

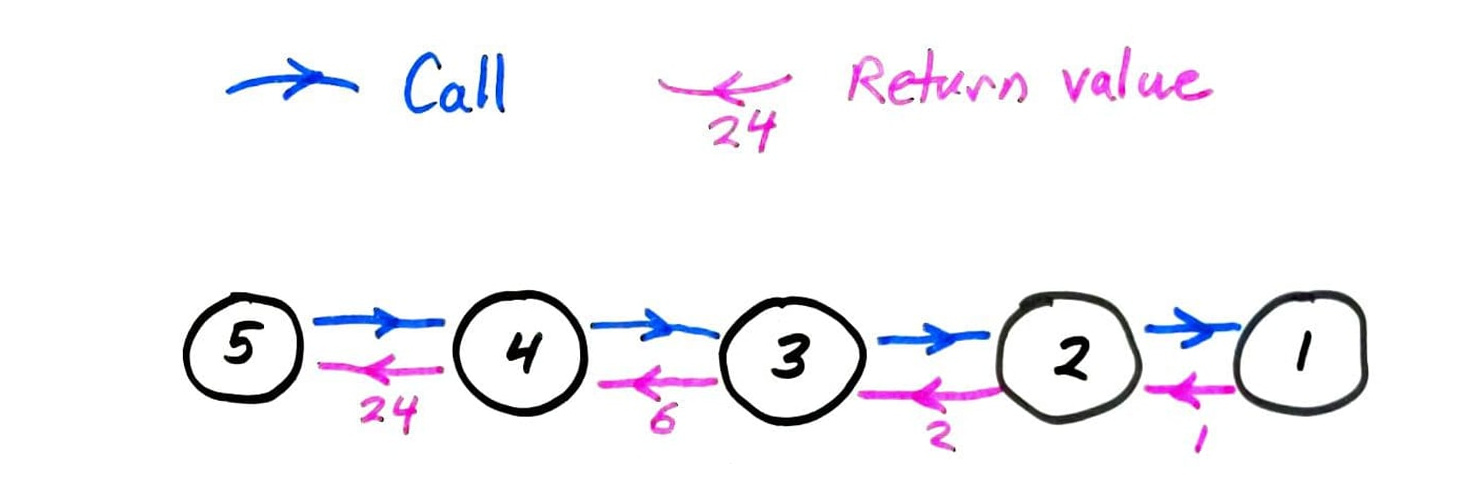
fib call graph
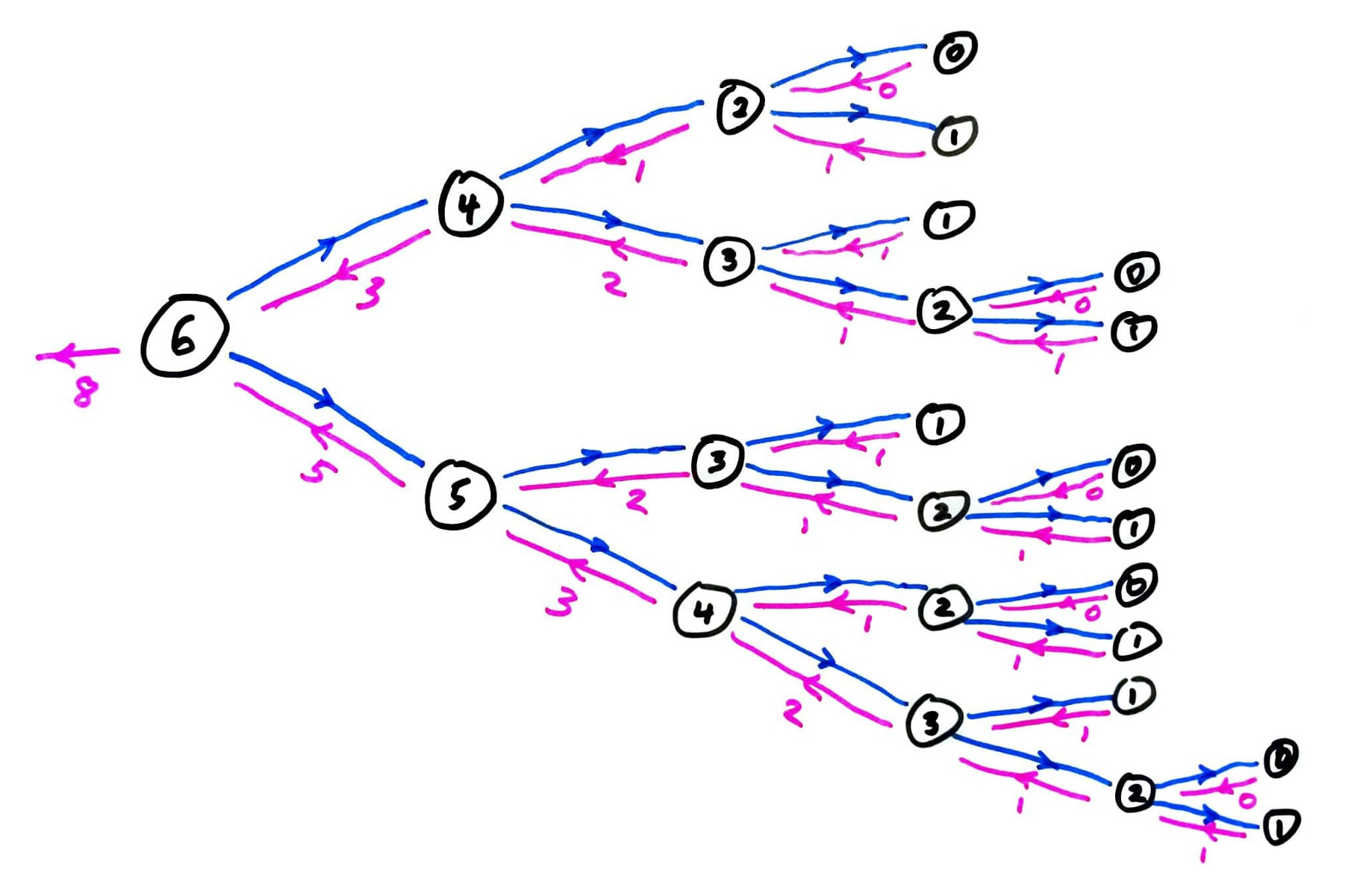
fib call graph
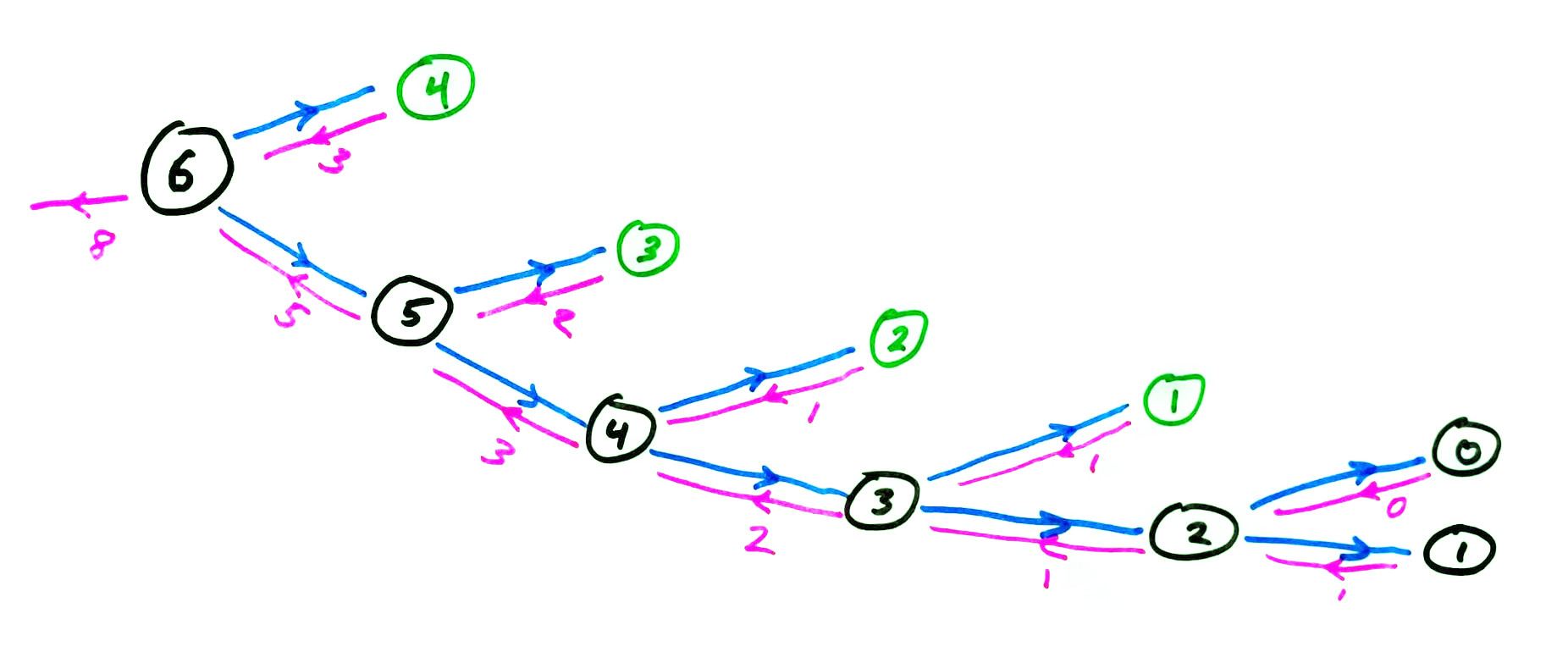
Memoization
fib computes the same terms over and over again.
Instead, let's store all previously computed results, and use the stored ones whenever possible.
This is called memoization. It only works for pure functions, i.e. those which always produce the same return value for any given argument values.
math.sin(...) is pure; random.random() is not.
memoized fib call graph

memoized fib call graph
Fibonacci timing summary
| n=35 | n=450 | |
|---|---|---|
| recursive (naive) | 1.9s | ≫ age of universe |
| recursive (memoized) | <0.001s | 0.003s |
| iterative | <0.001s | 0.001s |
Measured on my old office PC (2015, Intel i7-6700K) with Python 3.8.5
Memoization summary
Recursive pure functions with multiple self-calls often benefit from memoization.
Memoization does not alleviate recursion depth limits.
Memoization trades running time for memory consumption.
References
- Algorithms by Jeff Erickson, available as a free PDF, discusses some examples of recursion in Chapter 1.
- Lutz discusses recursive functions in Chapter 19 (pages 555-559 in the print edition).
- Intro to Python for Computer Science and Data Science by Deitel and Deitel discusses recursion in Chapter 11. The online version of this text is freely available to UIC students, faculty, and staff. (You will first need to log in with you UIC email.)
- The open textbook Think Python, 2ed, by Allen B. Downey discusses recursion in Sections 5.8 to 5.10.
- Computer Science: An Overview by Brookshear and Brylow discusses recursion in Section 5.5. (This book is often an optional text for MCS 260.)
Revision history
- 2023-02-06 Finalization of the 2023 lecture this was based on
- 2024-01-29 Initial publication
- 2024-02-06 Fix project 1 deadline